Дискретные цепи Маркова как модель эволюции систем

70. Дискретные цепи Маркова как модель эволюции систем.

            В теории случайных процессов Марковские процессы являются наиболее изученными. В настоящее время модели Марковских процессов широко используются при решении задач анализа и проектирования больших и сложны систем.

            Из всей совокупности процессов образующих класс Марковских наибольший интерес вызывают процессы с конечным числом состояний. Пусть имеется некоторая физическая система О, которая может принимать конечное число состояний S₁, S₂,…,S_n.

Опр. Процесс называется Марковским, если для каждого момента времени вероятность любого состояния системы в будущем, зависит только от состояния системы в настоящем и не зависит от того каким образом система пришла в это состояние.

            Другими словами, если состояние системы в момент времени t_k – S_i, и если вероятность перехода системы P_ij в момент времени t_k+1 в состояние S_j и не зависит от того в каких состояниях система побывала в моменты времени t_k-1, t_k-2…, то процесс называется Марковским. Последовательность переходов системы осуществляемая в соответствии с определением называется односвязной или простой цепью Маркова.

S₁₀®S₂®S₉®S_­3®…

Опр. Если вероятность перехода системы в состояние S_j в момент времени t_k+1 зависит от m предыдущих исходов, то цепь Маркова называется m-связной

Опр. Цепь Маркова называется дискретной если переход из одного состояния в другое происходит скачком только в определенные моменты времени через шаг Dt, который равен константе.

Состояние S₁, S₂,..,S_n условными вероятностями .

P^k – матрица переходных вероятностей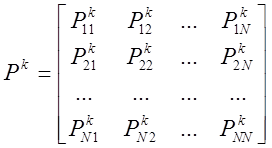

Для каждой строки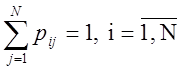

Если вероятность зависит от времени, то цепь Маркова называется однородной, в этом случае матрица переходных вероятностей имеет вид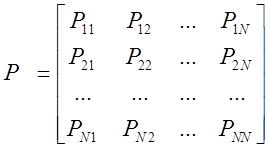

Предположим необходимо вычислить вероятность перехода системы из i-го состояния в j-ое через 2 шага

р(2)=р(1)²

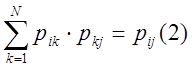
р(k)=p(1)² – вероятность

 Вероятность того, что система окажется в состоянии j – это вероятность будет равна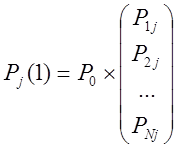

Для вычисления безусловной вероятности нахождения системы в состоянии j через N шагов необходимо умножить вектор-строку P(0) на вектор столбец матрицы P(N).