Геометрическая интерпретация задач ЛП и нелинейного программирования (НЛП). Гиперплоскость, полупространство. Область решений задач ЛП и НЛП

49. Геометрическая интерпретация задач ЛП и нелинейного программирования (НЛП). Гиперплоскость, полупространство. Область решений задач ЛП и НЛП

Область решений системы линейных неравенств

Пусть задано лин. нер-во: 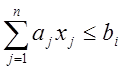(*), i =

D – множество решений системы линейных неравенств (*)

1.  Область допустимых решений задачи линейного программирования есть область решений системы линейных неравенств

2.  D – выпуклое множество

3.  Множество D – выпуклая многогранная область с конечным числом крайних точек, причем крайняя точка (угловая) это такая допустимая точка области M, которая не может быть представлена в виде выпуклой комбинации любых других точек этого множества

Свойства решений задачи линейного программирования

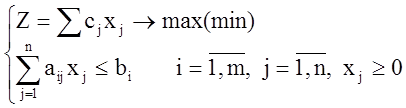(1)

Оптимальное решение задачи линейного программирования (1) находится в крайней точке многогранника D, определяемого ограничениями задачи (1).

Крайняя точка множества D – базисное решение задачи(1)

Теорема: Если оптимальное решение задачи (1) достигается более чем в 1 крайней точке, то оно достигается в любой точке являющейся выпуклой комбинацией упомянутой крайней точки