




Для определенности будем считать, что делимое ![]() и делитель
и делитель ![]() записаны
в позиционной системе счисления по основанию
записаны
в позиционной системе счисления по основанию ![]() . При
этом длины чисел
. При
этом длины чисел ![]() и
и ![]() равны,
соответственно,
равны,
соответственно, ![]() и
и ![]() .
.
Задача нахождения частного сводится к определению
приближенного значения дроби ![]() с точностью ½, с последующим
его округлением до ближайшего целого, и, возможно его уточнением. Уточнение
частного требуется, если округление приближенного значения дроби
с точностью ½, с последующим
его округлением до ближайшего целого, и, возможно его уточнением. Уточнение
частного требуется, если округление приближенного значения дроби ![]() происходит не в ту сторону. Пусть
происходит не в ту сторону. Пусть ![]() — полученное частное. Тогда
— полученное частное. Тогда ![]() , и, значит, искомое частное отличается от
полученного, не более чем на 1. Для уточнения частного вычислим остаток
, и, значит, искомое частное отличается от
полученного, не более чем на 1. Для уточнения частного вычислим остаток ![]() и, если
и, если ![]() , то
частное надо уменьшить на 1. Если
, то
частное надо уменьшить на 1. Если ![]() , то частное надо
увеличить на 1.
, то частное надо
увеличить на 1.
Приближенное значение дроби ![]() с
точностью до ½ можно получить как произведение
с
точностью до ½ можно получить как произведение ![]() на
приближенное значение дроби
на
приближенное значение дроби ![]() с точностью
с точностью ![]() . Последний факт следует из неравенства
. Последний факт следует из неравенства 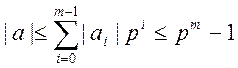 . В свою очередь, приближенное значение
дроби
. В свою очередь, приближенное значение
дроби ![]() можно получить, решая уравнение
можно получить, решая уравнение ![]() методом Ньютона (методом касательных).
методом Ньютона (методом касательных).
Пусть ![]() — некоторое начальное
приближение к дроби
— некоторое начальное
приближение к дроби ![]() . О методах выбора
. О методах выбора ![]() поговорим ниже. Допустим, на
поговорим ниже. Допустим, на ![]() -ой итерации построено приближение
-ой итерации построено приближение ![]() . Уравнение касательной в точке
. Уравнение касательной в точке ![]() к функции
к функции ![]() имеет
вид
имеет
вид ![]() . Точка пересечения касательной с осью
абсцисс равна
. Точка пересечения касательной с осью
абсцисс равна ![]() . Взяв эту точку в качестве
следующего приближения
. Взяв эту точку в качестве
следующего приближения ![]() , повторим процесс. И так до тех
пор, пока не будет достигнута требуемая точность приближения.
, повторим процесс. И так до тех
пор, пока не будет достигнута требуемая точность приближения.
Обозначим через ![]() погрешность
приближенного решения
погрешность
приближенного решения ![]() , т.е.
, т.е. ![]() .
При
.
При ![]() имеем
имеем ![]() , или
, или ![]() .
.
Из полученной рекуррентной формулы ![]() выводим
выводим
![]() или
или ![]() . Из
равенства
. Из
равенства ![]() вытекает, что величина
вытекает, что величина ![]() стремится к нулю с ростом k только
тогда, когда
стремится к нулю с ростом k только
тогда, когда ![]() .
.
Укажем способ выбора ![]() , при
котором выполняется неравенство
, при
котором выполняется неравенство ![]() . Положим
. Положим ![]() равным
равным ![]() , где
, где ![]() — ближайшее целое, не превосходящее дроби
— ближайшее целое, не превосходящее дроби ![]() . Трудоемкость вычисления значащих разрядов
. Трудоемкость вычисления значащих разрядов
![]() имеет порядок
имеет порядок ![]() . Далее,
. Далее,
![]() . Подставим вместо
. Подставим вместо ![]() выражение
выражение
![]() , где
, где ![]() ,
получим
,
получим ![]() . Поскольку в модуле стоит разность
одинаковых по знаку чисел, то
. Поскольку в модуле стоит разность
одинаковых по знаку чисел, то ![]() не превосходит
наибольшего из них. Так как
не превосходит
наибольшего из них. Так как ![]() и
и ![]() , то
, то ![]() .
.
Оценим число итераций метода Ньютона, необходимое для
достижения требуемой точности. Из равенства ![]() и
неравенства
и
неравенства ![]() выводим соотношение
выводим соотношение ![]() . Из неравенства
. Из неравенства ![]() и
и
![]() находим
находим ![]() , или
, или ![]() . Таким образом, число итераций методом
Ньютона не больше
. Таким образом, число итераций методом
Ньютона не больше ![]() .
.
Полученная оценка числа итераций метода Ньютона справедлива,
если на каждой итерации ![]() выполняется неравенство
выполняется неравенство
![]() .
.
Выполнение этих неравенств гарантировано при точном
вычислении ![]() по формуле
по формуле ![]() .
Однако, точное вычисление
.
Однако, точное вычисление ![]() по этой формуле
приводит к быстрому росту числа знаков после запятой. Чтобы избежать роста
числа знаков после запятой предлагается округлить
по этой формуле
приводит к быстрому росту числа знаков после запятой. Чтобы избежать роста
числа знаков после запятой предлагается округлить ![]() , но так
чтобы неравенство
, но так
чтобы неравенство ![]() сохранилось.
сохранилось.
Для определенности, пусть ![]() . В силу
выпуклости функции
. В силу
выпуклости функции ![]() величина
величина ![]() всегда
находится левее
всегда
находится левее ![]() , т.е.
, т.е. ![]() .
Действительно,
.
Действительно, ![]() . Таким образом, если округлить
величину
. Таким образом, если округлить
величину ![]() в сторону увеличения с точностью до
в сторону увеличения с точностью до ![]() , то неравенство
, то неравенство ![]() сохранится.
Обозначим через τ ошибку округления
сохранится.
Обозначим через τ ошибку округления ![]() . Тогда
. Тогда
![]()
![]() . Поскольку под модулем
стоит разность одинаковых по знаку чисел, то
. Поскольку под модулем
стоит разность одинаковых по знаку чисел, то ![]() .
Отсюда, учитывая неравенства τ<
.
Отсюда, учитывая неравенства τ<![]() и
и ![]()
![]()
![]() выводим
выводим
![]() .
.
Оценим трудоемкость k-ой итерации метода Ньютона (k
≥ 1). Из сказанного ранее следует, что xk-1
можно округлить в сторону возрастания с точностью до![]() . Таким
образом, число знаков после запятой xk-1 больше 2k-1+n.
Из неравенств
. Таким
образом, число знаков после запятой xk-1 больше 2k-1+n.
Из неравенств ![]() и b≥pn-1делаем вывод, что первые n-1 разрядов после запятой равны нулю. То
есть, число xk-1 представляется в виде
и b≥pn-1делаем вывод, что первые n-1 разрядов после запятой равны нулю. То
есть, число xk-1 представляется в виде ![]() , где zk-1 — целое число
по длине не больше 2k-1+1.
, где zk-1 — целое число
по длине не больше 2k-1+1.
Пусть трудоемкость умножения целых чисел длины s и l
равна Tу(s + l). Тогда трудоемкость вычисления xk
по формуле (2-bхk-1)хk-1 = (2![]() , с последующим округлением в
, с последующим округлением в ![]() разрядах по порядку определяется
величиной О(Tу(2k+n)). Общая
трудоемкость метода Ньютона не превосходит по порядку О
разрядах по порядку определяется
величиной О(Tу(2k+n)). Общая
трудоемкость метода Ньютона не превосходит по порядку О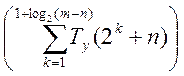 .
.
Приведем оценку трудоемкости операции деления методом
Ньютона в предположении, что умножение проводится с использованием быстрого
преобразования Фурье. В этом случае Tу(l) = О(l∙logl)
и вычисление xk лучше вести по формуле ![]() . При этом, образы
. При этом, образы ![]() ,
,
![]() вычисляются сразу. Потом над ними
проводятся соответствующие операции умножения, вычитания, и только после этого
восстанавливается результат. Поскольку
вычисляются сразу. Потом над ними
проводятся соответствующие операции умножения, вычитания, и только после этого
восстанавливается результат. Поскольку ![]() , то
длина произведения
, то
длина произведения ![]() не превосходит 2k-1+1+n.
Таким образом, трудоемкость k-ой итерации деления по порядку не
превосходит О
не превосходит 2k-1+1+n.
Таким образом, трудоемкость k-ой итерации деления по порядку не
превосходит О![]() , а, значит, трудоемкость всего
метода ограничена сверху величиной О
, а, значит, трудоемкость всего
метода ограничена сверху величиной О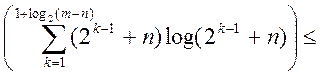 O(m
log m log (m-n)).
O(m
log m log (m-n)).
Тем самым доказана
Теорема. Трудоемкость деления чисел с остатком ограничена сверху величиной O(m log m log (m-n)).
Если числа а и b заведомо делятся друг на
друга, то можно воспользоваться версией метода Ньютона в р-адической
арифметике. В дальнейшем будем считать р простым числом. Если b
делится на pk, то его последние k разрядов равны 0.
Поскольку а делится на b, то а делится на pk.
Отбрасывая последние k нулевых разрядов чисел а и b,
приходим к задаче деления, где b не делится на р.
Так как р — простое число и b0≠0, то наибольший общий
делитель b0 и р равен 1. Расширенным алгоритмом
Евклида найдем числа u и v, что ub0+рv = 1. Положим х0 = u.
Далее проводим итерации метода Ньютона, вычисляя хk по
формуле хk = (2-хk-1b)хk-1![]() . Поскольку р — основание
системы счисления, то, по сути, мы проводим операции над младшими 2k
разрядами, отбрасывая старшие. Обозначим через ηk величину 1-bхk.
Индукцией по k покажем сравнение ηk ≡ 0
. Поскольку р — основание
системы счисления, то, по сути, мы проводим операции над младшими 2k
разрядами, отбрасывая старшие. Обозначим через ηk величину 1-bхk.
Индукцией по k покажем сравнение ηk ≡ 0 ![]() . При k = 0 имеем:
η0 = 1-bх0 ≡ 1- b0u
≡ 0(mod р). Пусть ηk-1≡0
. При k = 0 имеем:
η0 = 1-bх0 ≡ 1- b0u
≡ 0(mod р). Пусть ηk-1≡0![]() . Тогда, ηk=1-bхk
. Тогда, ηk=1-bхk![]() ≡1-b(2-хk-1b)хk-1
≡1-b(2-хk-1b)хk-1![]() ≡
≡
≡(1-bхk-1)2![]() ≡
≡![]() .
.
Единственным решением сравнения а ≡ bх(mod рm-n)
является частное а/b. Поэтому, не более чем через log2(m-n)+1
итерацию метода, частное будет найдено. Трудоемкость метода Ньютона в этом
случае не превосходит O(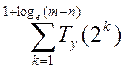 ). Если для умножения
используется быстрое преобразование Фурье, то Ту(l) = O(l
logl). Трудоемкость метода в этом случае оценивается величиной O(
). Если для умножения
используется быстрое преобразование Фурье, то Ту(l) = O(l
logl). Трудоемкость метода в этом случае оценивается величиной O(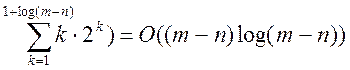 . Как видим, за счет более экономной схемы
умножения, трудоемкость деления чисел нацело, по порядку, имеет ту же
трудоемкость, что и умножение.
. Как видим, за счет более экономной схемы
умножения, трудоемкость деления чисел нацело, по порядку, имеет ту же
трудоемкость, что и умножение.
Тем самым доказана
Теорема. Трудоемкость
деления чисел без остатка ограничена сверху величиной ![]() .
.
•В лекции подробно разобраны быстрые алгоритмы деления.
•Приведены оценки трудоемкости.
Контрольные вопросы и упражнения:
•Возможность распараллеливания алгоритма деления.
•Как изменится алгоритм деления чисел без остатка, если основание системы счисления будет составное.
•Насколько принципиальный характер носит отличие верхних оценок трудоемкости алгоритмов деления с остатком и без остатка.
•Составить алгоритм деления целых чисел без остатка при основании равном 10.
•Составить алгоритм деления целых чисел без остатка при основании равном 2k.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.