Алгоритм восходящего восстановления дерева разбора. Понятие конфигурации. Связь между конфигурациями, состояниями и операциями восходящего акцептора, страница 2

Тогда движение автомата по этому правилу будет выглядеть так:

2.  Движение по правой части правила осуществляется операциями

2.1.  Сдвиг ( Shift ) S_n:

2.1.1.  занесение текущего входного символа в стек символов;

2.1.2.  чтение следующего входного символа;

2.1.3.  занесение номера состояния n в стек состояний;

2.1.4.  переключение автомата в состояние n.

2.2.  Переход ( Go ) G_n:

2.2.1.  занесение нетерминала, образованного в результате свертки, в стек символов;

2.2.2.  занесение номера состояния n в стек состояний;

2.2.3.  переключение автомата в состояние n.

3.  Если на верхушке стека символов образовалась основа, то выполняется свертка ( Reduce ) :

3.1.  Со стека символов сбрасывается ровно столько символов, сколько их в основе;

3.2.  Со стека состояний сбрасывается ровно столько же номеров состояний;

3.3.  Текущим устанавливается состояние, номер которого оказался на верхушке стека – C_b;

3.4.  На входе автомата (перед текущим терминалом) формируется нетерминал N из левой части правила.

После свертки будет выполняться операция Go, так как на входе оказался символ N.

Необходимое и достаточное условие выполнения свертки – переключение автомата в состояние C_k.

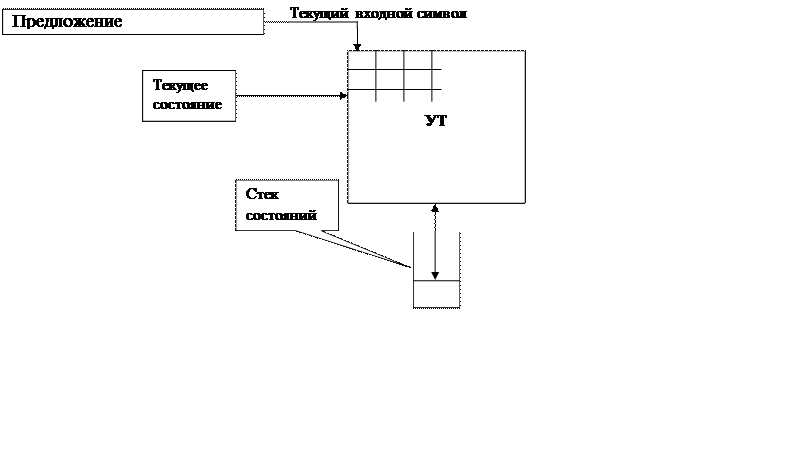Поэтому на самом деле стек символов не нужен.

И окончательно, смысл операций:

1.  Сдвиг ( Shift ) S_n:

1.1.1.  чтение следующего входного символа;

1.1.2.  занесение номера состояния n в стек состояний;

1.1.3.  переключение автомата в состояние n.

1.2.  Переход ( Go ) G_n:

1.2.1.  занесение номера состояния n в стек состояний;

1.2.2.  переключение автомата в состояние n.

2.  Свертка ( Reduce ) R_k,m:

2.1.  Со стека состояний сбрасывается k номеров состояний;

2.2.  Текущим устанавливается состояние, номер которого оказался на верхушке стека;

2.3.  В качестве текущей колонки УТ устанавливается колонка m.

3.  Операция Stop.

4.  Операция останова по ошибке.

Понятие конфигурации. Связь между конфигурациями,
состояниями и операциями восходящего акцептора

Пусть есть правило S : S + T.

Отметим маркером ▼ все возможные положения восходящего автомата в этом правиле:

S : ▼ S + T

S : S ▼ + T

S : S + ▼ T

S : S + T ▼

Каждая такая запись и называется конфигурацией.

1.  Начальному состоянию автомата соответствует конфигурация Z : ▼ S „.

2.  Если какому-либо состоянию автомата поставлена в соответствие конфигурация N : a ▼ M b , где a и b - произвольные цепочки (например – конфигурация Z : ▼ S „), и для нетерминала M есть правила:

M : γ ₁

M : γ ₂

...

M : γ _n ,

то этому же состоянию автомата соответствуют такие дочерние (или порожденные) конфигурации:

M : ▼γ ₁

Грамматика G a1
0	Z: Su
1	S : S + T
2	S : T
3	T : T * F
4	T : F
5	F : ( S )
6	F : i <идентификатор>
7	F : c <константа>

M : ▼γ ₂

...

M : ▼γ _n

Таким образом, состоянию 0 автомата по грамматике G _a1 будут соответствовать:

Z : ▼S u

S : ▼S + T

S : ▼T

T : ▼T * F

T : ▼F

F : ▼( S )

F : ▼i

F : ▼c

3.  Если в некоторой конфигурации данного состояния маркер находится перед терминалом, например

R : j ▼ t y

то автомат (в тот момент, когда он находится в этом состоянии и на входе имеет этот терминал) должен выполнить операцию сдвига с переключением в строго определенное другое состояние и чтением следующего терминала со входа. Применительно к конфигурациям это означает, что состоянию, в которое осуществляется переключение, соответствует конфигурация R : j t ▼ y.