Код Грэя
При отсутствии статистической взаимосвязи между элементами (буквами) сообщения конструктивные методы построения эффективных кодов были даны впервые Шенноном, Фэно и Хаффменом (см. разд. 4.4), однако такие коды вызывают затруднения при декодировании. Этого недостатка в некоторой степени лишены рефлексные коды (от латинского reflexio — отражение). Характерной особенностью таких невзвешенных кодов является то, что любые две соседние n-значные кодовые комбинации отличаются друг от друга лишь в одной позиции. Наиболее часто применяемым является рефлексный код Грея (1878 год), который получается из натурального кода путем суммирования его двоичной комбинации по модулю 2 с той же комбинацией, сдвинутой на один разряд вправо, и последующим отбрасыванием младшего разряда сдвинутой комбинации. Например, для
цифры 7 (0111) в коде Грея будем иметь: 0111Å 0011 =0100.
Если составить таблицу натурального кода и кода Грея для десятичных чисел 0—15, то можно отметить следующие его особенности.
1.Каждая последующая комбинация всегда отличается от предыдущей только в одной позиции (в одном разряде).
2. Смена значений элементов в каждом разряде (1 на 0 или 0 на 1) при переходе от комбинации к комбинации в коде Грея происходит вдвое реже, чем в натуральном. Так, в натуральном коде смена элемента первого (младшего) разряда происходит с чередованием элементов 0 — 1 — 0 — 1..., второго — с чередованием 00— 11— 00 — 11..., третьего — с чередованием 0000—1111—0000... В коде Грея соответственно имеем: для первого разряда 11 — 00 — 11..., для второго 0000 —1111 — 0000... Это свойство кода Грея позволяет при том же быстродействии схемы кодирования получать точность кодирования выше по сравнению с натуральным кодом.
3. При сложении двух соседних комбинаций кода Грея по модулю 2 (mod 2} число единиц равно числу разрядов минус три, т. е. в нашем случае имеем одну единицу. В общем случае, для n-значного кода число единиц равно n - 3. Это свойство кода Грея иногда можно использовать для проверки правильности принятых комбинаций.
4. В коде Грея можно выделить оси симметрии (оси «отражения»), относительно которых наблюдается идентичность элементов в некоторых разрядах. Так, например, имеет место симметрия относительно оси, проведенной между числами 7 и 8. В комбинациях, симметричных относительно этой оси, идентичны три символа младших разрядов, относительно осей 1—2, 5—6, 9—10, 11—12 имеется симметрия в одном символе младшего разряда, а относительно осей 3—4 и 11—12 — в двух символах. Эта особенность и послужила основанием для использования термина «рефлексный» (или отраженный) код.
По сравнению с натуральным рефлексный код Грея позволяет уменьшить ошибки неоднозначности считывания, а также ошибки, вызванные помехами при передаче информации по каналам связи. Если, например, неправильное воспроизведение символа старшего разряда комбинации натурального кода приводит к значительной ошибке, то для кода Грея эта ошибка составляет величину одного младшего разряда.
Схема преобразователя 4-разрядного натурального кода в код Грея (рис. 4.8) состоит из генератора слова программы EWB 4.1, регистра сдвига на D-триггерах Т0 — ТЗ с индикаторами их состояния (и входного натурального кода) на логических пробниках 0—3, логических элементов ИСКЛЮЧАЮЩЕЕ ИЛИ ХОR0—XOR3, ИЛИ OR0—OR3, И &0 — &3, на выходе которых включены индикаторы кода Грея на логических пробниках 2^0—2^З. Схема И &с служит для формирования тактовых импульсов сдвига, поступающих на v-входы триггеров; на вход Хс схемы &с подаются разрешающие логические сигналы 1 с первого (левого) выхода генератора слова, а на вход С — тактовые сигналы с его выхода Clk. Кодовые комбинации в натуральном коде ХО—ХЗ задаются на дисплее генератора в ячейках, соответствующих выходам 5—2. Для вывода двоичной комбинации в коде Грея на индикаторы 2^0—2^3 используется логический сигнал Х&.с восьмого выхода генератора.
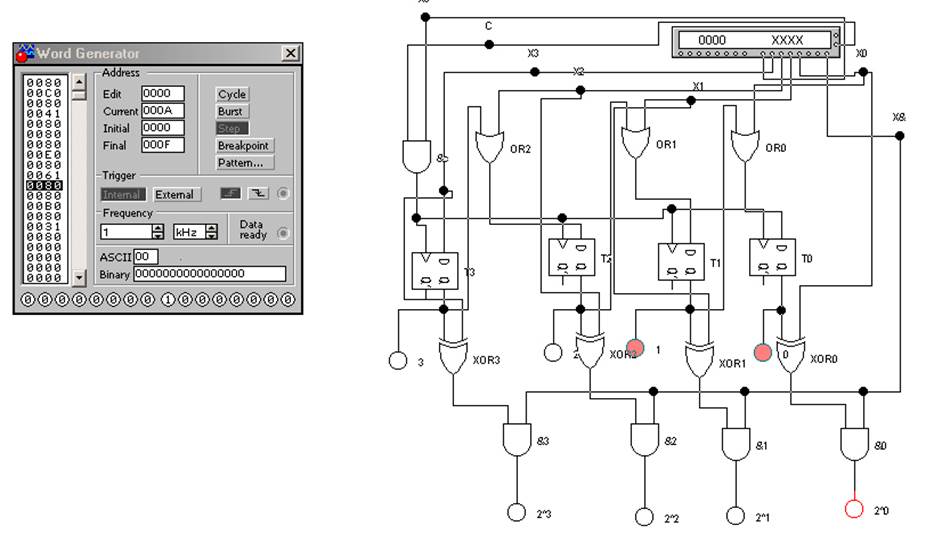
Рис. 4.8. Преобразователь натурального кода в код Грея
В кодовой комбинации № 0 (см. лицевую панель генератора) производится
очистка регистра от предыдущей комбинации 14 входного кода путем сдвига вправо. При комбинации № 1, получаемой, после нажатия кнопки STEP, в регистре запоминается натуральный код 1000, при комбинации № 2 он сдвигается вправо на один разряд, т. е. равен 0100. При комбинации № 3 опять выдается код 1000, который с помощью элементов XOR0—XOR3 суммируется по модулю 2 с запомненным на регистре при комбинации № 2 (выполняется операция 0100 Å 1000 = 1100). Поскольку при комбинации № 3 присутствует сигнал Х& = 1, то полученный результат (код Грея) через &0—&3 выводится на индикаторы 2^0 – 2^3. При комбинациях 4—6 производится очистка регистра от кода 0100 (три сдвига вправо). При комбинации № 7 вводится натуральный код 1100, при комбинации № 8, он сдвигается на один разряд вправо (получаемый при этом код 0110 на рис. 4.2 отображается индикаторами 3 - 0), при комбинации № 9 выполняется операция 0110Å1100 = 1010 с выводом результата на индикаторы 2^0—2^3. Аналогичным образом производится преобразование кода 0110 (комбинация № 12) в. код Грея 0101 (комбинация № 14).
Недостатком кода Грея и других рефлексных кодов являются трудности обработки данных с помощью ЭВМ и существенное усложнение декодирующих устройств, что приводит к необходимости предварительного преобразования рефлексных кодов в натуральный. В случае кода Грея это преобразование производится по следующему правилу: если преобразование начинается со старшего разрядов кода, то символ старшего разряда записывается без изменения, каждый следующий символ кода Грея инвертируется, если в натуральном коде перед этим был получен символ 1, или оставляется без изменения, если в натуральном коде был получен символ 0.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.