Технологический расчет оборудования отделения десорбции и абсорбции хлористого водорода, страница 2

1. Находим концентрации распределяемого компонента в газе (y) и жидкости (x) на входе и на выходе из аппарата в массовых долях:

;     ;

;         

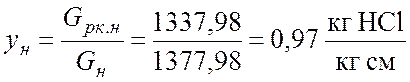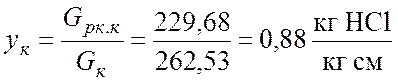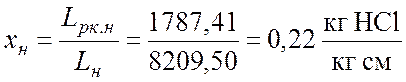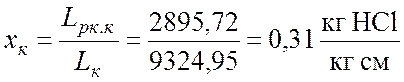
Концентрации распределяемого компонента в газе (Y) и жидкости (X) на входе и на выходе из аппарата в относительных массовых долях:

;;

;

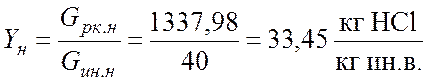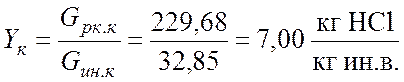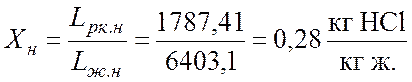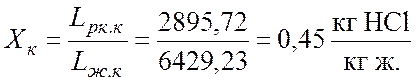
где G_ин.н = G_н(1 - y_н) = 1377,98×(1-0,97) = 40 кг/ч и G_ин.к = G_к(1 – y_к) = 262,53×(1-0,88) = 32,85 кг/ч – расходы инертного вещества газовой фазы на входе и на выходе из аппарата; L_ж.н = L_н(1 - x_н) = 8209,5×(1-0,22) = 6403,1 кг/ч и L_ж.к = L_к(1 – x_к) = 9324,95×(1-0,31) = 6429,23 кг/ч – расходы абсорбтива на входе и на выходе из аппарата.

2. Построение равновесной линии процесса абсорбции

Построение равновесной линии в координатах Y(Y^*)-X производится при помощи уравнения Генри, которое в случае выражения концентраций в относительных массовых долях имеет вид:

,                                               

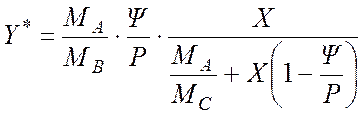где M_A, M_B, M_C – соответственно молекулярные массы распределяемого компонента, инертного вещества газовой фазы и воды, кг/кмоль; Ψ – константа Генри, мм.рт.ст; Р –абсолютное давление в системе, мм.рт.ст.

          Молекулярные массы:

·  распределяемого компонента (хлористого водорода), М(НСl) = 36,5 кг/кмоль;

·  инертного вещества газовой фазы (С₂Н₅Сl), М(С₂Н₅Сl) = 64,5 кг/кмоль;

абсорбента (воды), М(Н₂О) = 18 кг/кмоль.

При температуре жидкости 20 ⁰С константа Генри Ψ = 2100 мм.рт.ст.[]. Давление в системе Р = 740 мм.рт.ст.

Задаемся значениями X в интервале от 0 до 0,5 с шагом 0,1 и по уравнению Генри находим значения Y^*.

X₀ = 0;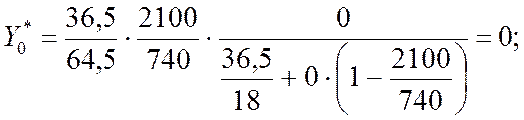          

X₁ = 0,1;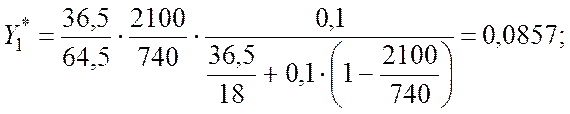 

X₂ = 0,2;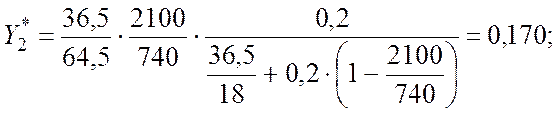 

X₃ = 0,3;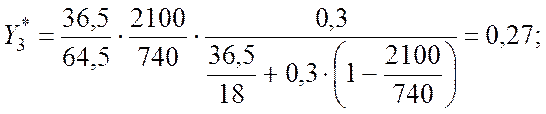 

X₄ = 0,4;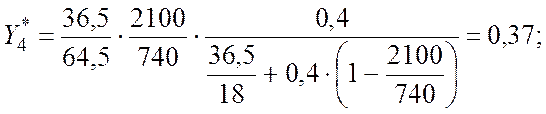 

X₅ = 0,45;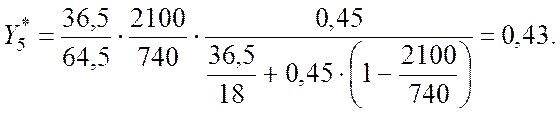 

По выражениям 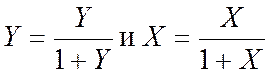 пересчитаем концентрации, выраженные в относительных массовых долях (Y, X) в концентрации, выраженные в массовых долях (y, x):

Y,кгНСl/кг смеси	0	0,079	0,145	0,213	0,270	0,301
X, кг НСl/кг смеси	0	0,091	0,17	0,23	0,286	0,31

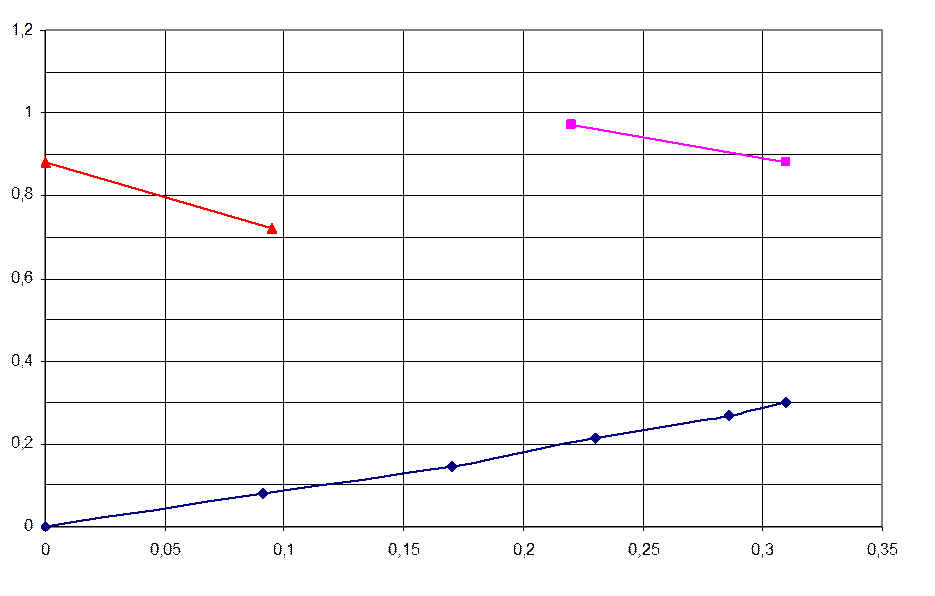
Рис. 3.4. Рабочая и равновесные линии процесса абсорбции хлористого водорода: А-В- получение крепкой соляной кислоты, C-D- получение слабой соляной кислоты.

3. Расчет поверхности теплообмена для абсорбера крепкой соляной кислоты

3.1.  Расчет критерия Рейнольдса производим по формуле:

                                                                

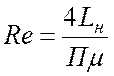
где L_н – расход жидкой фазы, кг/с; П – смоченный периметр сечения абсорбера, м; μ – коэффициент динамической вязкости, Па×с.

Смоченный периметр:

                                                                    

где d_вн – внутренний диаметр трубок, м; n – количество труб.

Последовательно задаемся числом, диаметром и длиной труб и находим смоченный периметр абсорбера и критерий Рейнольдса:

d_вн = 0,06 м;          n = 566 шт;           ℓ = 3 м;

= 1,3×10^-3 Па×с.

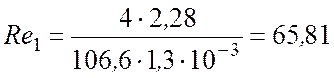
Результаты расчетов сводим в таблицу 3.1.

Таблица 3.1

№	dвн, м	n, шт	l, м	П, м	Re	F, м2
1	0,06	566	3	106,6	77,8	320
2	0,06	280	3	71,59	115,8	200
3	0,06	93	3	17,5	202	50
4	0,06	130	4	24,5	304	98
5	0,04	130	4	16,3	456	120
6	0,04	93	4	11,68	640	98

3.2.  Определение толщины пленки по формуле/10/:

                                                    

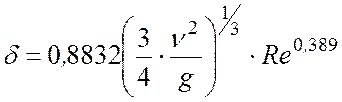
где n - коэффициент кинематической вязкости, м²/с; g= 9,81 м/с² – ускорение свободного падения

                                      

                                      

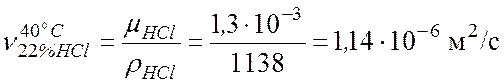
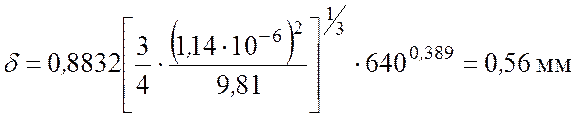
3.3.  Расчет критерия Прандтля.

                                                                  

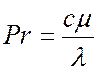
где с – теплоемкость раствора, Дж/кг×К; l - коэффициент теплопроводности раствора, Вт/м×к. = 2639 Дж/кг×К; = 0,48 Вт/м×К.

                                                 

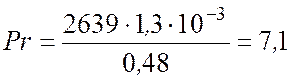
3.4.  Определение критерия Нуссельта.

Значение критерия Nu определяем по номограмме /10/ по найденным значениям критериев Re и Pr. Nu = 7.

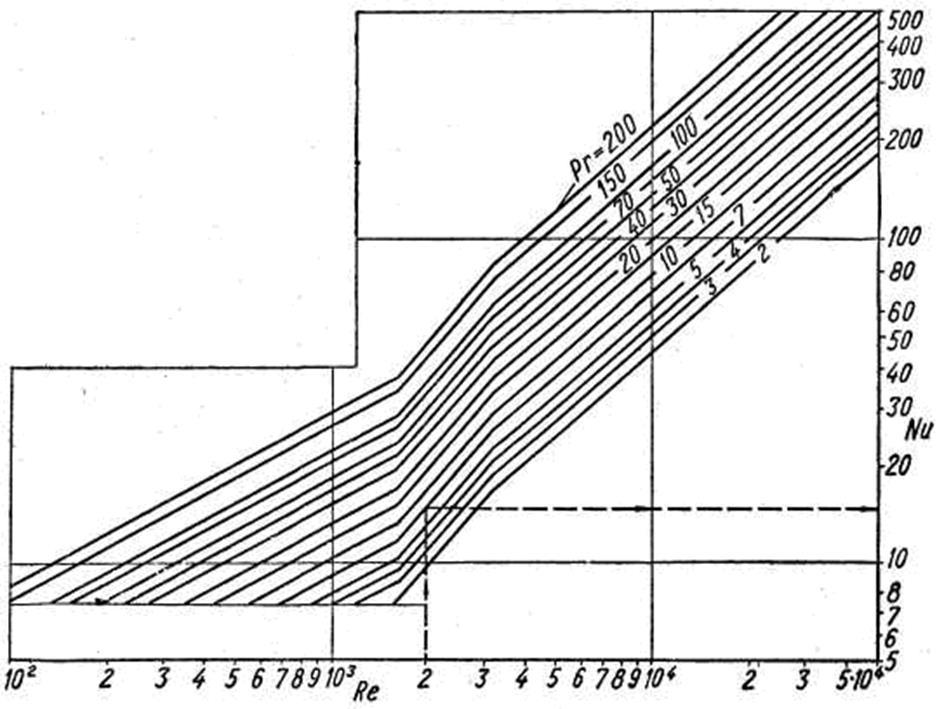
Рис. 3.5. Номограмма для определения критерия Нуссельта Nu в зависимости от числа Рейнольдса Re и критерия Прандтля Рг при гравитационном течении пленки по вертикальной поверхности