Планирование и обработка результатов полного факторного эксперимента, страница 3

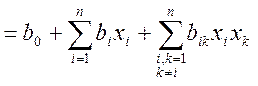                                 Ŷ                                                           (10)

Например, при n=3:

                                 Ŷ                     (11)

Для определения коэффициентов b_ik (эффектов парного взаимодействия) необходимо расширить матрицу планирования (табл.1), дополнив её столбцами произведений факторов (табл.2).

                                                                                Таблица 2.

№ опыта	X1	X2	X3	X1X2	X1X3	X2X3	Y
1	-1	-1	-1	+1	+1	+1	Y1
2	+1	-1	-1	-1	-1	+1	Y2
3	-1	+1	-1	-1	+1	-1	Y3
4	+1	+1	-1	+1	-1	-1	Y4
5	-1	-1	+1	+1	-1	-1	Y5
6	+1	-1	+1	-1	+1	-1	Y6
7	-1	+1	+1	-1	-1	+1	Y7
8	+1	+1	+1	+1	+1	+1	Y8

Задание: проверьте, выполняются ли свойства матрицы, приведённые выше, для столбцов произведений.

    Эффекты парного взаимодействия определяются аналогично линейным эффектам: 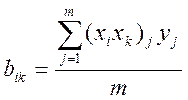                              ,                                            (10)

Значимость эффектов взаимодействия оценивается так же, как и значимость линейных эффектов.  Адекватность неполной квадратичной модели (11) проверяется по критерию Фишера. Если модель адекватна, цель, поставленная в лабораторной работе, достигнута. Если же модель неадекватна, это означает, что эксперимент поставлен в области, близкой к экстремуму  поверхности отклика, и    в уравнение регрессии следует ввести квадраты факторов. Однако для оценки квадратичных эффектов уже недостаточно ПФЭ, необходимо использовать планы второго порядка.  

 

2.Постановка задачи.

Объектом исследования согласно цели работы является химический реактор. Химический реактор – это аппарат, предназначенный для получения определённого продукта химической реакции. Отношение количества полученного в реакторе продукта к максимально возможному количеству по реакции, называется выход продукта (Y), Yизмеряется в долях единицы или в %.  Выход продукта зависит от концентраций реагентов (C₁иC₂), температуры в реакторе (Т) и времени протекания реакции (τ).  Для постановки эксперимента выберем факторы иопределим область экспериментирования. Предположим, что в эксперименте будут варьироваться  Т,  τ иC₂, а концентрация C₁ будет постоянной (C₁ = 1.44 моль/л).  Зададим значения факторов в центре плана (Z_i⁰):

                  Т = 350К,   τ = 11мин,C₂ = 1моль/л

 и интервалы варьирования по каждому фактору (ΔZ_i):

                        Δ Т = 10К,   Δ τ = 1мин,    ΔC₂ = 0.2моль/л.

Таким образом, в нашем случае число факторов: n = 3 и число опытов  в полном факторном плане:   N = 2³ = 8. Откликом является выход продукта Y(%). Задача лабораторной работы заключается в том, чтобы составить план эксперимента, выполнить эксперимент в соответствии с планом, выполнить регрессионный анализ результатов для линейной модели (7) и неполной квадратичной модели (11), проанализировать полученные результаты и дать конкретные  рекомендации относительно окончательного выбора модели реактора.

3. Алгоритм решения задачи.

В соответствии со стратегией планирования эксперимента, рассмотренной в математическом анонсе, для достижения поставленной в лабораторной работе цели необходимо:

1.  составить план полного факторного эксперимента в кодированных факторах (табл.1);

2.  перейти к плану в  размерных факторах по формуле (5);

3.  выполнить эксперимент, в котором условия опытов  задаются в соответствии с планом эксперимента, и измеряется значение отклика (эксперимент выполняется на модели реактора, реализованной в виде специальной программы);

4.  по результатам эксперимента идентифицировать линейную регрессионную модель (7):

·  рассчитать коэффициенты по формулам (8),

·  рассчитать погрешность коэффициентов по формуле (9), для расчёта дисперсии измерения отклика  выполнить L опытов в центре плана;

·  проверить значимость коэффициентов по Стьюденту;

·  проверить адекватность модели по Фишеру;