Распространение декаметровых радиоволн, страница 5

 Определение  оптимальных  рабочих  частот  и  составление  расписания  смены частот. Наиболее простым способом определения оптимальных частот является применение ионосферных карт (рис. 12.2., 12.3.). При постоянной электронной концентрации максимальные и критические частоты связаны законом секанса (12.54):

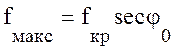                                          ,                                       (15.7)

где  φ₀ – угол падения волны на слой ионосферы.

Для заданной протяженности радиолинии величину φ₀ можно определить с помощью теорем эквивалентности, заменяя криволинейную траекторию волны ломаной линией с вершиной в точке отражения. Формула для определения φ₀ имеет вид (15.6);

                               ,                         

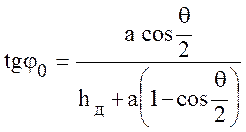где  h_д – действующая высота отражающего слоя,

       Θ – геоцентрический угол, определяемый из выражения (13.2):

,

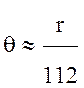где  r – в км.

Сведения о действующей высоте отражающего слоя публикуется в прогнозах радиоволн.

Поскольку сведения о состоянии ионосферы в виде ионосферных карт составляются с интервалом 2 часа, то с их помощью не представляет труда составить график суточного хода максимальных частот, и на этом основании составить график суточного хода оптимальных рабочих частот. На приемные радиоцентры также регулярно поступают краткосрочные прогнозы радиоволн, дающие оперативную информацию об оптимальных частотах на данной радиолинии.

На протяженных радиолиниях волна в пункт приема приходит несколькими скачками. В этом случае определяют максимальные частоты для всех точек отражения и в качестве максимальной частоты выбирают минимальное значение.

Определение  множителя  ослабления. Все методы расчета напряженности поля в диапазоне декаметровых волн являются полуэмпирическими, так как в расчет входит ряд величин, полученных экспериментально. Наиболее распространенным методом определения множителя ослабления является метод, разработанный А.Н. Казанцевым.

По А.Н. Казанцеву формула для определения множителя ослабления имеет вид:

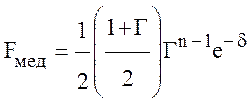                     ,                         (15.8)

где Г – модуль коэффициента отражения от поверхности Земли,

       n – количество отражений от ионосферы,

       δ – суммарный коэффициент поглощения в слоях ионосферы.

Число отражений n, испытываемых лучом на трассе протяженностью r, определяется по формуле:

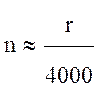                               ,                                              (15.9)

где  r – в км.

В знаменатель формулы (15.8) введен множитель 2, что соответствует уменьшению поля на 6 дБ. Из них 3 дБ А.Н. Казанцев относит за счет того, что приемная антенна имеет линейную поляризацию, а луч в процессе отражения от ионосферы приобретает эллиптическую поляризацию. Еще 3 дБ обусловлены потерями при расщеплении луча.

Множитель 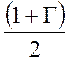   учитывает влияние отраженной от земли волны в месте расположения приемной антенны. Если бы приемная антенна А (рис.15.5.) находилась на оптимальной высоте h над поверхностью Земли, то лучи 1 и 2 имели бы одинаковую фазу и напряженность результирующего поля (при горизонтальной поляризации) определялась бы по формуле  , где Е₀ – поле прямого луча. В реальных условиях вследствие изменений высоты отражающего слоя обеспечить выполнение оптимальных условий не представляется возможным, и А.Н. Казанцев берет среднее значение коэффициента, учитывающего влияние отраженного луча, а именно, 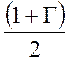 . Обычно величина Г очень близка к единице, и потому можно положить 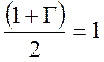 . А.Н. Казанцев рекомендует выбирать значение Г порядка 0,8.

Третий множитель учитывает потери при отражении от поверхности Земли в промежуточных точках. Для односкачковых линий связи   подобные отражения отсутствуют, и  Г ^n-1=1.

Четвертый множитель учитывает поглощение в ионосфере. Суммарный коэффициент поглощения δ определяется из формулы:

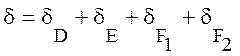                                     ,                                  (15.10)

в которой учитывается поглощение при двукратном прохождении слоев D, E, F₁ и поглощение в отражающем слое F₂. Если отражение происходит от слоя F₁, то формула для коэффициента поглощения примет вид: