Разработка основных технических решений по проектированию аналоговой системы передачи (АСП) с ЧРК, работающей по коаксиальному кабелю, страница 2

            Расчётная формула для мощности суммарных помех от нелинейных переходов 2-го порядка имеет вид:

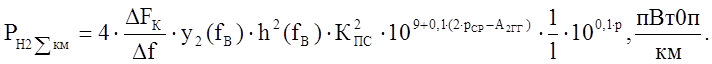    ( 3 )

            Аналогично ( 2 ) обозначим:

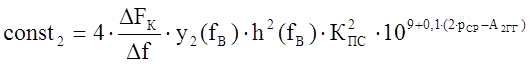     ( 3а )

            Где: DF_к = 3,4 - 0,3 = 3,1 кГц - полоса частот канала ТЧ;

            Df = f_в - f_н = 13708 - 812 = 12896 кГц - ширина линейного спектра АСП.

            у₂ ( f_в, b, Dр ) - коэффициент, отражающий распределение мощности помех 2-го порядка в линейном спектре, в нашем случае b=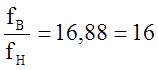, следовательно у₂(f_в)=6,0×10^-2

            h²( f_в ) - коэффициент, отражающий воздействие на спектральное распределение помех наличия частотно-зависимой отрицательной связи в линейном усилителе; расчет для типичного значения перепада усиления в спектре сигнала  Dа = 10 дБ дает величину h²( f_в ) = 2,55 ед.

            Р_ср =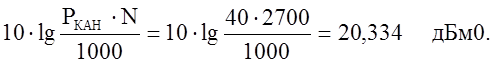 - уровень средней мощности группового сигнала в ТНОУ, равный при числе каналов N ³ 240 абсолютному уровню суммы средних мощностей в ТНОУ.

            Зависимость в ( 3 ) от длины усилительного участка имеет вид 1/ l, 1/ км. Третий сомножитель в ( 3 ) показывает, что при повышении уровня передачи мощность помех от нелинейности 2 порядка экспоненциально возрастает.

            Сложение мощности помех от нелинейных переходов 3 порядка 1 рода в пределах секции ОУП - ОУП по квадратичному закону приводит формулу к следующему виду:

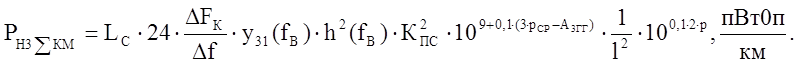      ( 4 )

            Как и ранее, обозначим:

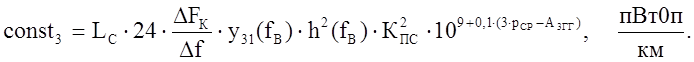 ( 4а )

Где у₃₁( f_в; Dр = 13 дБ ) = 0,81 - коэффициент, отражающий распределение мощности помех 3 порядка 1 рода. Зависимость j₃( l ) от длины усилительного участка имеет вид 1/ l².

Третий сомножитель в ( 4 ) показывает, что при повышении уровня передачи р мощность помех 3 порядка возрастает по закону экспоненты с удвоенным показателем.

            Суммарная мощность помех, равна сумме мощностей, рассчитанных по ( 2 ), ( 3 ) и ( 4 ). Однако, как указано в ( 4, с. 137, 138 ), в верхних по спектру каналах АСП при наличии предискажений помехами 2 порядка можно пренебречь:

      ( 5 )

            Увеличение уровня передачи в ( 5 ) уменьшает первое слагаемое и увеличивает второе. Для фиксированной длины усилительного участка l существует такой оптимальный уровень передачи Р_опт, при котором суммарная мощность помех минимальна. Его можно найти, приравняв нулю производные обеих частей ( 5 ) и решая уравнение относительно р. Введём в ( 5 ) обозначение х = 10^0,1р; выражение ( 5 ) примет вид:

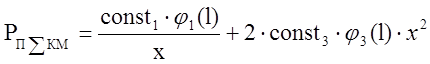      ( 6 )

            Выполним дифференцирование обеих частей ( 6 ) по х:

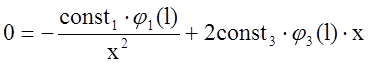
            Полученное уравнение решим относительно х, действительный корень полученного уравнения является оптимальным значением уровня передачи р:

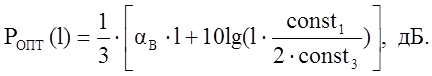 ( 7 )

            Максимально допустимую длину усилительного участка l_max определим, решая уравнение ( 1 ) графически рис.7:

            Задаём рациональные длины усилительного участка l₁ ( от 8 до 1,5км) и рассчитываем по ( 7 ) значение р_олт( l ). Подставляя численные значения получим:

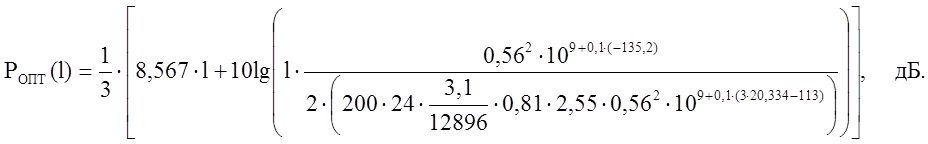
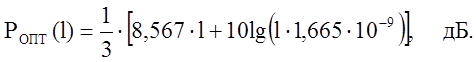
            Полученные результаты сводим в таблицу1, на основании которой строим график зависимости(рис.7) и Р_ПåКМ от l (рис.8).

Таблица 1.