Министерство РФ по связи и информатизации
Сибирский Государственный Университет
Телекоммуникаций и информатики
по курсу АПТС
«Анализ графовой модели СЭГ»
Выполнил:
студент III курса ЗО (ускор.)
специальности «СС и СК»
студ. билет № 021 ТУ - 192
Яровой Р.А. гр. ЗТ-26
Проверила:
Прохорова Н.И.
Вариант 1 – в 7.
Анализ графовой модели СЭГ.
Задание:
1. Дать теоретико-множественное представление модели сети по заданному геометрическому графу (рисунок 1.1).
2. Определить расстояние от вершины с минимальным номером до вершины с максимальным номером по графовой модели.
3. Определить кратчайшую связывающую сеть по алгоритму Прима-Краскала.
4. Составить матрицу инцидентности вершин .
5. Составить матрицу смежности вершин. Исходные данные:
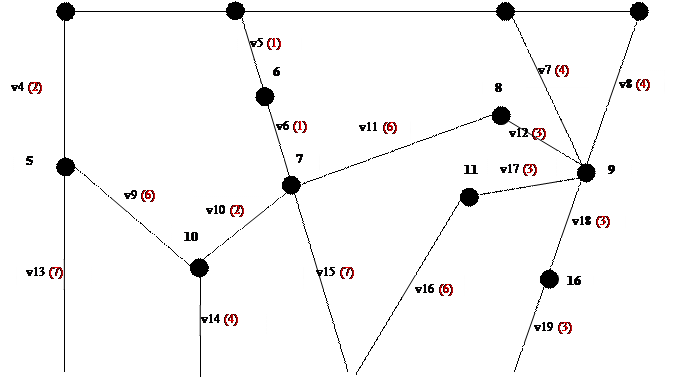
Задан план городского населенного пункта.
Цифры около вершин размеченной графовой модели будущей СЭГ - это номера вершин.
Цифры в скобках, вблизи каждого ребра модели – это веса этих ребер.
1 2 3 4
v1 (5) v2 (8) v3 (4)
 |
![]()
![]()
![]()
![]()
![]()
v20 (5) v21 (4) v22 (5)
12 13 14 15
Рисунок 1.1: Графовая модель.
Решение:
1. Теоретико-множественное представление модели сети:
Вершины графа : 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 .
Ребра графа: v1, v2, v3, v4, v5, v6, v7, v8, v9, v10, v11, v12, v13, v14, v15, v16, v17, v18, v19, v20, v21, v22.
v1 (1; 2) v9 (5; 10) v17 (9; 11)
v2 (2; 3) v10 (7; 10) v18 (9; 16)
v3 (3; 4) v11 (7; 8) v19 (15; 16)
v4 (1; 5) v12 (8; 9) v20 (12; 13)
v5 (2; 6) v13 (5; 12) v21 (13; 14)
v6 (6; 7) v14 (10; 13) v22 (14; 15)
v7 (3; 9) v15 (7; 14)
v8 (4; 9) v16 (11; 14)
2. Определить расстояние от вершины с минимальным номером (1) до вершины с максимальным номером (16) по графовой модели.
В графовой модели расстояние между вершинами равно длине кратчайшей цепи (ρ).
ρ = v4 – v13 – v20 – v21 – v22 – v19 = 3 + 7 + 5 + 4 + 5 + 3 = 27
ρ = v4 – v9 – v14 – v21 – v22 – v19 = 3 + 6 + 4 + 4 + 5 + 3 = 25
ρ = v4 – v9 – v10 – v11 – v12 – v18 = 3 + 6 + 2 + 6 + 3 + 3 = 23
ρ = v1 – v2 – v3 – v8 – v18 = 5 + 8 + 4 + 4 + 3 = 24
ρ = v1 – v2 – v7 – v18 = 5 + 8 + 4 + 3 = 20
ρ = v1 – v5 – v6 – v11 – v12 – v18 = 5 + 1 + 1 + 6 + 3 + 3 = 19
ρ = v1 – v5 – v6 – v15 – v22 – v19 = 5 + 1 + 1 + 6 + 5 + 3 = 21
ρ (1; 16) = 19
3. По алгоритму Прима-Краскала определить кратчайшую связывающую сеть.
Вариант 1:
1 Шаг: Упорядочим ребра графовой модели по убыванию весов: 8,7,7,6,6,6,5,5,5,4,4,4,4,4,3,3,3,3,2,2,1,1;
2 Шаг: Рассмотрим последовательно все ребра графа, начиная с ребра наибольшего веса, и определим, можно ли их удалить из графа, не нарушив его связности.
Суммарный вес ребер:
Σреб = 7 + 6 + 6 + 5 + 4 + 4 + 4 + 3 + 3 + 3 + 3 + 2 + 2 + 1 + 1 = 54
Вариант 2:
1 Шаг: Упорядочим ребра графовой модели по возрастанию весов:
1,1,2,2,3,3,3,3,4,4,4,4,4,5,5,5,6,6,6,7,7,8;
2 Шаг: В соответствии с ориентировочным рядом последовательно решить вопрос включить ли в будущее остовное дерево новое ребро, если при таком включении может образоваться цикл, то ребро не включаем. Первое в ряду ребро включаем обязательно в остовное дерево.
Суммарный вес ребер:
Σреб = 1 + 1 + 2 + 2 + 3 + 3 + 3 + 3 + 4 + 4 + 4 + 5 + 6 + 6 + 7 = 54
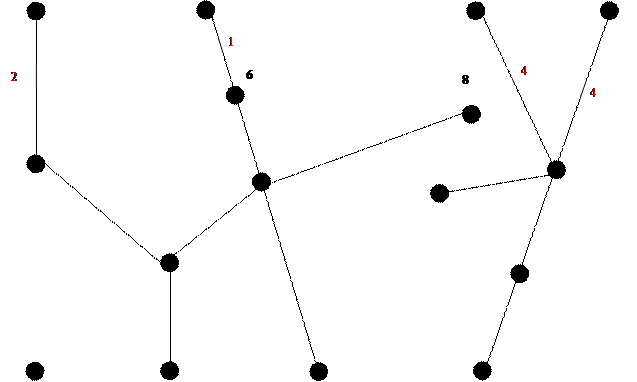
Кратчайшую связывающую сеть изобразим на рисунке 1.2.
1 2 3 4
 |
|
|
|

|
|||||||||||||||||||||||
|
|||||||||||||||||||||||
|
|||||||||||||||||||||||
|
|||||||||||||||||||||||
|
|||||||||||||||||||||||
 |
|||||||||||||||||||||||
|
|||||||||||||||||||||||
|
|||||||||||||||||||||||
|
|||||||||||||||||||||||
|
|||||||||||||||||||||||
12 13 14 15
Рисунок 1.2: Кратчайшая связывающая сеть.
Литература:
1. Конспект лекций.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.