Анализ графовой модели СЭГ, страница 3

· определить экцентриситеты всех вершин;

ε(1)	ε(2)	ε(3)	ε(4)	ε(5)	ε(6)	ε(7)	ε(8)	ε(9)	ε(10)	ε(11)	ε(12)	ε(13)	ε(14)	ε(15)	ε(16)	а(17)	а(18)
32	26	28	25	19	20	25	22	20	19	18	23	27	21	25	26	26	26

· Диаметр d (G) = 32, радиус r (G) = 18

· Периферийная вершина-1…., центральная вершина-11.

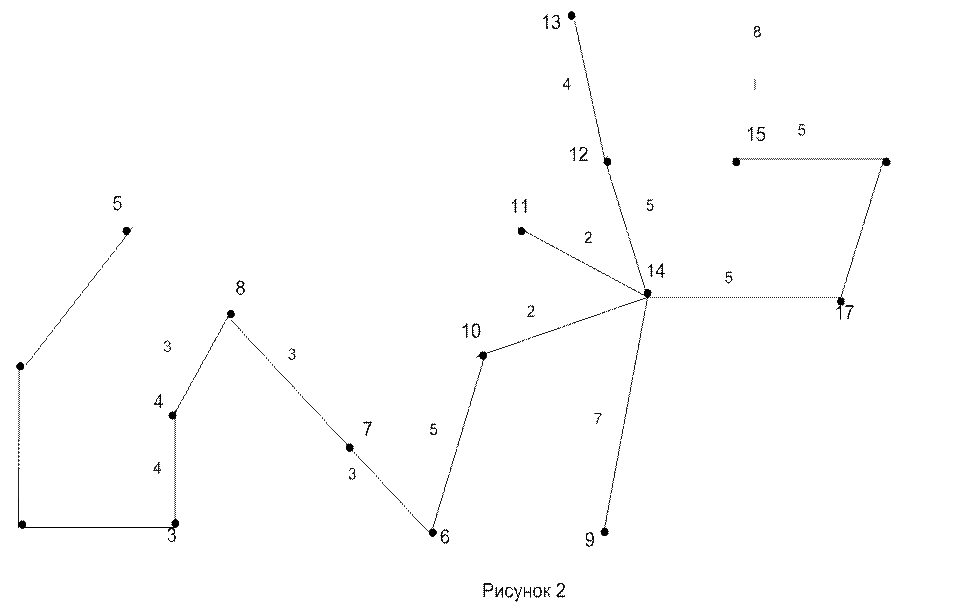
3.По алгоритму Прима-Краскала построить кратчайшее остовное дерево с минимальным суммарным весом ребер.

Решение.

1). Упорядочим ребра графа по убыванию весов: 9,8,7,7,7,7,7,5,5,5,5,5,5,5,5,5,5,4,4,4,4,4,3,3,3,2,2;

2). Рассмотрим последовательно все ребра графа начиная с ребра наибольшего веса и определим, можно ли их удалить из графа, не нарушив его связности.

Кратчайшее остовное дерево рисунок 1.

Суммарный вес ребер Σvреб = 85

Литература:

1 2 3