Схематизация условий разработки и основные гидродинамические расчеты показателей разработки при жестководонапорном режиме, страница 5

6)  полосовая залежь предполагается неограниченной по ширине или же принимают, что ее границы перпендикулярны рядам скважин [6].

При решении задач по определению дебитов рядов скважин при их совместной работе оказывается, что максимальный суммарный дебит при любой расстановке рядов и скважин можно получить, эксплуатируя

одновременно три ряда скважин. Если все скважины  трех рядов работают при одинаковом забойном давлении, то дебит второго ряда составит примерно 30-40 %, а третьего – 15-20 % от дебита первого ряда. Четвертый ряд практически прироста в дебите не дает, и средства на бурение и освоение скважин этого ряда не оправдываются [5].

Гидродинамические расчеты по определению дебитов рядов скважин в случае круговой залежи проводятся по формулам, также полученным исходя из принципов электроаналогии [6].

Аналогично полосообразной залежи в расчетах для круговой применяют понятие приведенного контура питания:

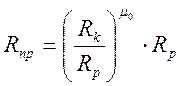 ,                                         (13)

где R_p – расчетный контур питания, определяемый по формуле:

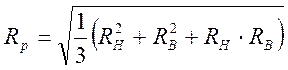 ,                       (14)

.

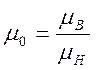Дебит одной скважины, работающей в круговой батарее, определяется по формуле:

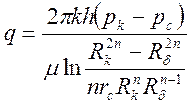 ,                                   (15)

где р_к и р_с – соответственно давления на контуре кругового пласта и в скважинах; R_к и R_б –соответственно радиус контура питания и радиус батареи скважин; r_с – радиус скважин; n – число скважин в батарее, причем

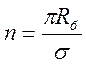            , (16)

где σ – половина расстояния между скважинами.

Если принять R_к >> R_б, то

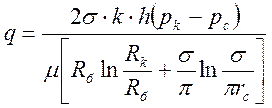 .                             (17)

Причем 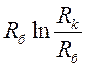= R_c , а  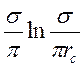= R₁, где R_c является внешним, а R₁ – внутренним сопротивлениями скважины.

Суммарный дебит всех скважин, работающих в круговой батарее (дебит ряда) определяется по формуле:

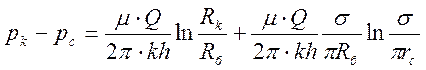 ,       (18)

где 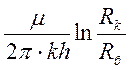        =Ω                                          (19)

 – внешнее сопротивление рядов, а  

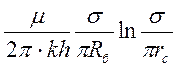=ω                                   (20)

– внутреннее. Причем полное сопротивление потоку движущейся жидкости между рядами будет  равно 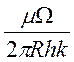, в призабойной зоне - 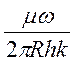[5].

         Общая схема составления системы уравнений остается аналогичной полосообразной, но в случае круговой залежи внешние и внутренние сопротивления рядов изменяются [5].

Сложный фильтрационный поток к одной скважине в круговом пласте можно разделить на плоскорадиальный от контура до круговой галереи и плоскорадиальный к скважине внутри галереи. Приток ко всем скважинам аналогичен параллельному соединению проводников с одинаковым сопротивлением R=ω+Ω.

Для круговой залежи также целесообразно одновременная работа не более чем трех рядов.

Приведенные методы гидродинамических расчетов для полосообразных и круговых залежей позволяют при различных вариантах расстановки рядов скважин определить суммарные отборы и дебиты каждой скважины.

Для определения оптимальных условий разработки необходимо рассматривать не менее трех вариантов размещения, для которых должна быть определена продолжительность эксплуатации и экономическая эффективность разработки [5].

3. РАСЧЁТНАЯ  ЧАСТЬ 

3.1  Задача по схематизации полосовой залежи.

Задача 1 (вариант 5)

Привести залежь «А» с размещёнными на ней скважинами к расчётной схеме полосовой залежи (рис 3.1).

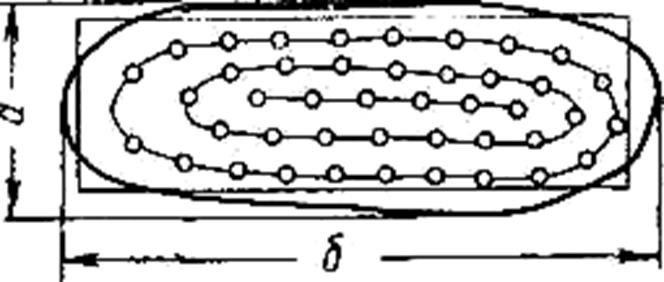
Рис. 3.1 Приближенная схема реальной залежи.

Исходные данные:

Длина залежи в =  17,5 км, ширина а = 4.5 км.

Расстояния от контура нефтеносности до первого ряда скважин равно L₁=700 м, расстояние от первого до второго равно L₂=700 и равно L₃= L₄= L₅  = L₆ =700м. Расстояние между скважинами в рядах  равны  2δ1=2δ2=2δ4=2δ5=600 м, 2δ3= 500 м.

Общий объём нефтенасыщенных пород в пределах внешнего контура нефтеносности V_общ. = 1026,3, объём пород между внешним контуром нефтеносности и первым рядом V₁ = 194,5м³, между первым и вторым рядом  V₂ = 180 м³ , между вторым и третьим    –   V₃ = 157 м³, между третьим и четвертым    –    V₄ = 150м³,  между четвёртым и пятым   -  V₅ = =165,3 м³, между пятым рядом скважин и внешним контуром нефтеносности   V₆ = 179,5м³.