Исследование симметричного вибратора, страница 5

Многолепестковый    характер     диаграммы направленности объясняется интерференцией полей элементарных излучателей, входящих в состав симметричного вибратора. Если длина вибратора 2ℓ не превышает λ, то  вся совокупность элементарных излучателей представляет собой синфазную неравноамплитудную решетку. Пусть точка наблюдения находится на окружности радиуса r (рис.4.6). При условии, что к >> 1, радиусы – векторы от элементарных источников до точки наблюдения без большой погрешности можно принять как систему параллельных линий. При j = 0 расстояние от отдельных элементарных излучателей до точки наблюден практически одинаковы, поэтому будут одинаковы и фазы полей,  создаваемых этими излучателями в точке наблюдения.

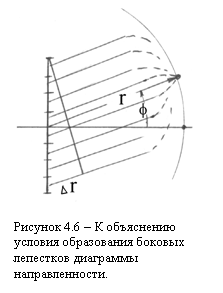
Если точка наблюдения сместится по окружности на некоторый угол j, то из-за возникшей при этом разности хода Dr поля в точке наблюдения будут сдвинуты по фазе на определенный угол. Причем наибольший сдвиг фаз будут иметь поля, создаваемые крайними элементами  вибратора. Если длина вибратора превышает λ, то в плечах вибратора появляются участки с противоположным направлением тока. В результате этого  фаза поля, создаваемого каждым элементарным излучателем в пункте наблюдения, будет определяться не только рассстоянием  до точки наблюдения, но  также фазой питающего тока.

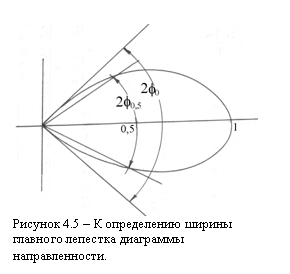
При разности хода полей от крайних элементов Dr, кратной 0,5l (Dj = mp, m = 1, 2, 3…), в диаграмме направленности вибратора будут минимумы, а при Dr, кратной l (Dj = m ^. 2p) - максимумы. Остальные участки плеч вибратора влияют в основном на уровень боковых лепестков. Теперь становится понятным, почему диаграммы направленности вибратора длиной    и 2ℓ = l не имеют боковых лепестков. Таким образом, именно электрическая длина вибратора определяет количество боковых лепестков.

Подобные рассуждения остаются справедливыми  при анализе диаграммы направленности любых антенн ( включая антенные решетки и антенны поверхностного типа).

Для согласования симметричного вибратора с питающей линией (фидером) необходимо знать его входное сопротивление, т.е. отношение . Подобно двухпроводной линии симметричный вибратор можно рассматривать как электрическую цепь с распределенными  параметрами R, L, С. Используя математический аппарат, описывающий процессы в длинной линии, можно записать:

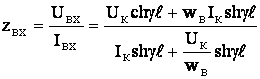                                  ,                       (4.3)

где I_к, U_к – ток и напряжение в конце линии (на концах вибратора),

      w_в – волновое сопротивление линии (вибратора)

              g = a + jк – постоянная распространения, 

              a - коэффициент затухания,

              к = .

По определению для линии 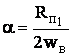                                                  (4.4)                   

Где: R_п1 – погонное сопротивление потерь.

Эта формула справедлива и для вибратора, однако в отличие от длинной линии потери энергии, подводимой к вибратору, определяются преимущественно не потерями на тепло (нагрев проводов), а излучением полезной мощности, т.е.

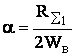                                                   ,                                        (4.5)