Исследование рупорных антенн, страница 2

где  F₁(j, Δ) – диаграмма направленности элемента Гюйгенса.

В плоскости Е выражение для F₁(j) имеет вид:

                                  ,                      (2)

а в плоскости Н

                                                           (3)

Здесь ½Г½ - модуль коэффициента отражения от открытого конца рупора, который при расчете можно принять равным нулю. Так как обычно у Е-секториального рупора L_Е >> l, а у Н-секториального рупора L_Н >> l, то множители, учитывающие направленные свойства элемента Гюйгенса в Е и Н плоскостях принимают вид:

F₁(j) = 1 + cos j  - для плоскости Е;

F₁(D) = 1 + cos D  – для плоскости Н.

Для удобства расчетов раскрыв рупора как излучающую поверхность можно представить в виде непрерывной плоскостной решетки, состоящей из элементов Гюйгенса.

Множитель F_с(j,D), определяющий направленные свойства этой решетки, зависит от распределения амплитуды и фазы поля в раскрыве рупора. Для достаточно длинного рупора с относительно малыми размерами раскрыва, поле в раскрыве можно в первом приближении считать синфазным.

Распределение амплитуды поля в раскрыве рупора такое же, как в  сечении питающего волновода. Для основного типа волны Н₁₀ распределение поля в плоскостях Е и Н показано на  рис. 2.

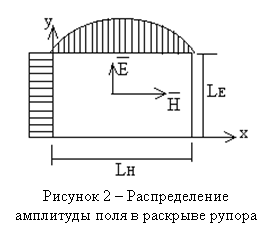Как видно из рис. 2,  в плоскости Е раскрыва рупора распределение амплитуды равномерное, и множитель решетки без учета фазовых искажений определяется по формуле:

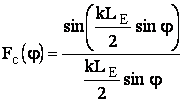                      (4)

В плоскости Н амплитуда распределяются по закону 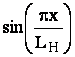, т.е. поле в центре раскрыва максимально, а на краях равно нулю. В соответствии с этим множитель решетки для плоскости Н:

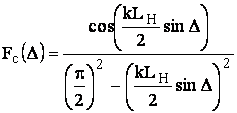                                                                (5)

Максимальные значения множителя системы в плоскости Е

(формула 4) соответствуют значениям аргумента синуса в числителе кратным :

               ,                                                              (6)

где    m = 0,1,2,3…, а минимальные значения соответствуют значениям аргумента синуса кратные p :

                                                                                  (7)

Соответственно, для плоскости Н максимумы множителя системы (5) соответствуют условию :

                                                                                      (8)

а минимумы – условию          

                                                                                    (9)

         Следует отметить, что уменьшение амплитуды поля к краям раскрыва рупора в плоскости Н ведет к расширению основного лепестка диаграммы направленности, что объясняется уменьшением эквивалентного раскрыва в этой плоскости. При этом однако значительно снижается интенсивность бокового излучения. При синусоидальном распределении амплитуд уровень бокового лепестка составляет примерно 2%, а при равномерном распределении – 7% от максимального уровня основного лепестка.

Из сказанного следует, что, если рупор имеет квадратный раскрыв (L_Е = L_Н), то в плоскости Е диаграмма направленности будет уже, чем в плоскости Н, а уровень боковых лепестков в плоскости Е больше, чем в плоскости Н.