Исследование параболических антенн, страница 3

                                 F(φ)=,                                                   (2)

где

 J₁ – функция Бесселя первого рода первого порядка от аргумента (kRsinφ ),

R – радиус раскрыва.

   Реальные распределения амплитуды поля по раскрыву не имеют строгого аналитического выражения и часто аппроксимируются выражением

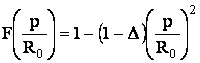                             ,                                           (3)

где

 Δ(«пъедестал»)- отношение амплитуды напряженности поля на краю зеркала к амплитуде поля в центре.

  Соответственно, ДН  антенны рассчитывается по формуле

                                .                                                       (4)

Здесь

F₁(φ)-ДН элемента Гюйгенса,

F_c(φ)- множитель системы:

                                F_c(φ)= Δ,                                  (5)

где:

J₁ и J₂ функции Бесселя первого рода первого и второго порядка, а u= kRsinφ  ,

  - множитель, определяющий ДН элемента Гюйгенса при расчетах ДН антенны обычно не учитывают из –за слабого влияния.

    Коэффициент направленного действия параболической антенны определяется по формуле для плоских синфазных поверхностей

                                            ,                                                (6) 

 где

S – площадь  раскрыва,

 ν  (КИП) – коэффициент использования поверхности раскрыва:

                                              ν=.                                                  (7)

Эффективной (действующей) площадью раскрыва S_эфф называется площадь эквивалентной синфазной и равноамплитудной  поверхности, излучающей такую же мощность, что и данная антенна.

Результирующий КИП приближенно можно представить произведением двух множителей

                                              ν=ν₁ν₂                                                      (8)

где

ν₁  - апертурный КИП,

ν₂  - коэффициент перехвата.

Апертурный КИП зависит от закона распределения амплитуды поля в раскрыве. Коэффициент перехвата определяется направленными свойствами облучателя и геометрией зеркала и определяет долю мощности облучателя, падающую на зеркало в пределах его угла раскрыва. Иными словами, коэффициент перехвата определяет  неиспользуемую часть мошности облучателя, за счет «переливания» энергии через край зеркала.

   Коэффициент направленного действия параболической антенны можно вычислять по приближенной формуле

                                           Д=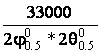                                           (10)

где

2φ , 2θ    и    ширина главного лепестка ДН антенны по половинной мощности вградусах в двух взаимно ортогональных плоскостях. В случае линейно-поляризованной волны это плоскости Е и Н.

    Поляризация волны, излучаемой параболической антенной, зависит от поляризационных свойств облучателя. Антенна с облучателем в виде симметричного вибратора излучает линейно-поляризованную волну. Вектор Е волны с осью вибратора находится в одной плоскости. Эта плоскость называется плоскостью поляризации волны. Параболическая антенна со спиральным облучателем излучает волну с круговой поляризацией. Положение вектора Е излучаемой волны в этом случае в течение одного периода высокой частоты изменяется, делая полный оборот в плоскости, нормальной направлению распространения. Конец вектора Е при вращении плоскости поляризации волны описывает замкнутую кривую в виде круга. Реально кривая имеет форму эллипса. Отношение малой полуоси эллипса к большой полуоси называется коэффициентом равномерности поляризационного эллипса. В случае линейной поляризации коэффициент равномерности равен нулю, в случае круговой – единице.