![]() 267.
267.
Коэффициент передачи датчика тока:
![]()
Принимаем настройку соответствующую математическому оптимуму:
![]() .
.
Определяем сопротивление RТ и RЗС:
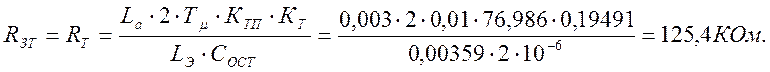
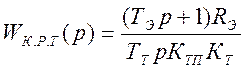 - передаточная функция ПИ-регулятора
тока
- передаточная функция ПИ-регулятора
тока
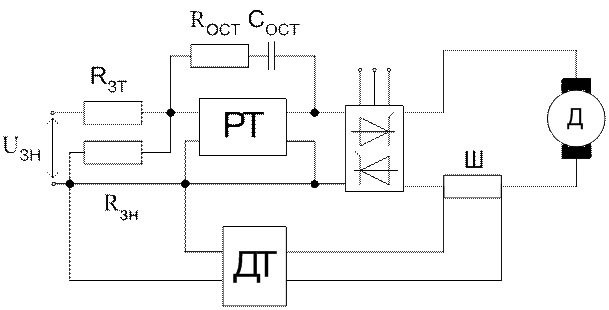
Рисунок 2.1 - Упрощённая принципиальная схема ПИ-регулятора тока
2.2.3 Расчёт параметров ПИ-регулятора скорости
Передаточный коэффициент тахогенератора:
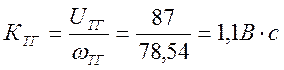
ЭДС тахогенератора при номинальных оборотах двигателя:
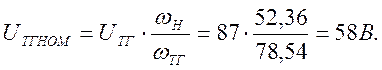
Коэффициент обратной связи по скорости:
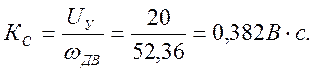
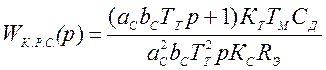 - передаточная функция ПИ-регулятора
скорости,
- передаточная функция ПИ-регулятора
скорости,
где aC = bC = 2 – при настройке контура на симметричный оптимум.
Максимальное ограничивающее напряжения для VD1 и VD2 рассчитываем по следующей формуле:
![]() В.
В.
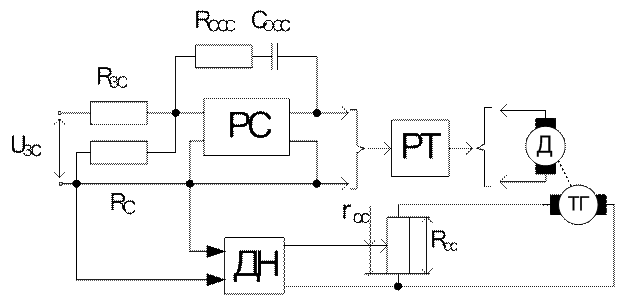
Рисунок 2.2 - Упрощённая принципиальная схема ПИ-регулятора скорости
2.2.4 Анализ структурной схемы системы регулирования скорости электропривода подъёмной установки
Рассмотрим двух контурную систему подчинённого регулирования управляемый выпрямитель – двигатель постоянного тока, структурная схема которого показана на рисунке 2.3. Объект регулирования в данном случае двигатель, который представлен последовательным соединением инерционного и интегрирующего звеньев, охваченных обратной связью по э. д. с. Во многих случаях, когда электромагнитная постоянная времени ТМ ≥ 4·Тμ, обратной связью по э. д. с. можно пренебречь. Исходя из структуры объекта, система двухконтурная, с внешним контуром скорости и подчинённым ему контуром тока якоря. Некомпенсируемые постоянные времени привода Тμ входят в передаточную функцию тиристорного преобразователя ТП. Объектом управления внутреннего контура служит тиристорный преобразователь, а объектом регулирования – двигатель с входом по напряжению якорной цепи и выходом по току.
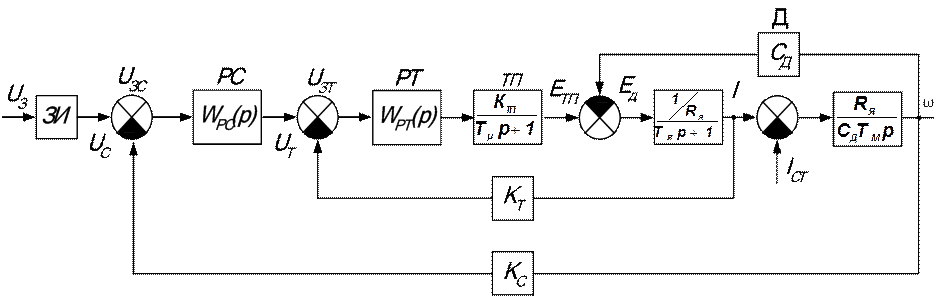
Рисунок 2.3 – Структурная схема системы подчинённого регулирования управляемый выпрямитель – двигатель постоянного тока
Передаточные функции звеньев имеют следующий вид:
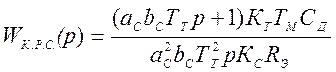 - передаточная функция ПИ-регулятора
скорости
- передаточная функция ПИ-регулятора
скорости
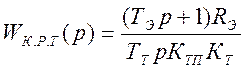 - передаточная функция ПИ-регулятора
тока
- передаточная функция ПИ-регулятора
тока
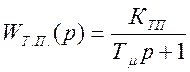 - апериодическое звено, моделирующее
тиристорный преобразователь
- апериодическое звено, моделирующее
тиристорный преобразователь
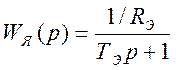 - апериодическое звено, моделирующее
якорную цепь двигателя
- апериодическое звено, моделирующее
якорную цепь двигателя
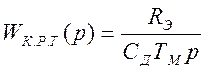 - интегрирующее звено, моделирующее
механическую инерцию двигателя
- интегрирующее звено, моделирующее
механическую инерцию двигателя
2.2.5 Анализ разомкнутой системы
Для построения логарифмических частотных характеристик необходимо последовательно найти передаточные функции внутренних контуров, после чего получить передаточную функцию разомкнутого контура скорости.
Во многих случаях, когда ТМ ≥ 4·Тμ, обратной связью по ЭДС можно пренебречь, после чего можно легко найти передаточную функцию замкнутого контура тока:
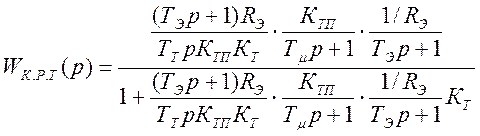 ,
,
где ТТ = 2·Тμ – при оптимизации контура тока по математическому оптимуму
После очевидных преобразований получим:
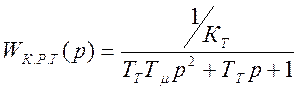
В связи с тем, что нам требуется найти передаточную функцию разомкнутого контура по управляющему воздействию, то возмущающее воздействие (МС) можно считать равным нулю. Таким образом, конечная передаточная функция разомкнутого контура скорости имеет следующий вид:
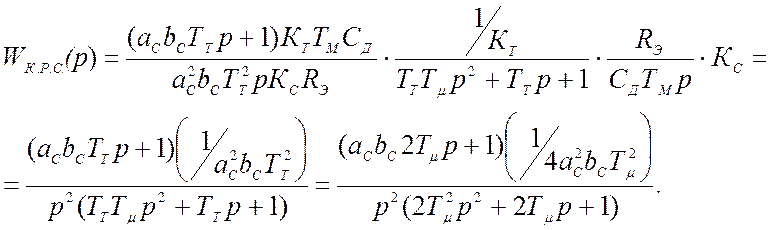
В знаменатели данной передаточной функции ярко выражено колебательное звено, т.е. для получения логарифмической функции необходимо привести выражение колебательного звена к стандартному виду, а именно:
![]() , где q = 1/Т = 1/√2∙0,01 = 70,71(ω =
1,85 дек.).
, где q = 1/Т = 1/√2∙0,01 = 70,71(ω =
1,85 дек.).
Воспользуемся стандартными методами решения, применяемыми в алгебре, получим:
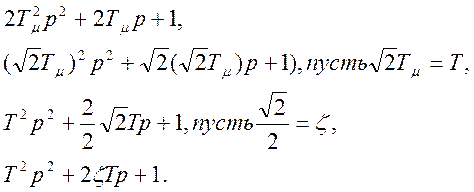
Далее получаю логарифмическую и фазо- частотную функцию для передаточной функцией с преобразованным колебательном звеном.
Применение логарифмических частотных характеристик позволяет упростить решение задачи синтеза САУ, потому что при этом значительная часть расчётов может быть заменена простыми графическими построениями.
Построение логарифмической частотной характеристики производится асимптотически по формуле, полученной из выражения как модуль комплексной передаточной функции:
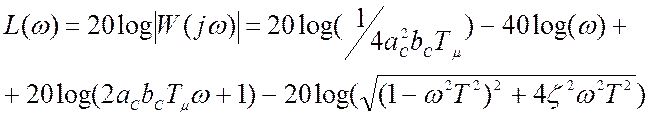 .
.
Фазочастотная характеристика определяется как аргумент комплексной передаточной функции:
φ(ω) = 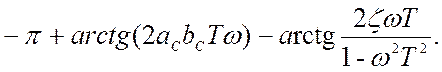
Подставив в полученные функции значение постоянных коэффициентов:
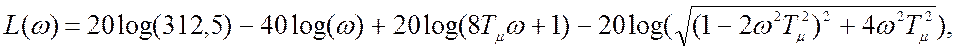
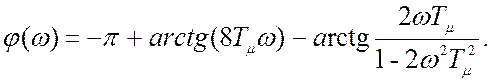
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.