Геология \ Проведение горных выработок

Отработка пологопадающих пластов средней мощности па базе комплекса 10КГ170Б, страница 2

Остаточные напряжения в сочетании с напряжениями от горного давления приводят к изменению расчетных схем металлоконструкций крепей и отдельных элементов, к существенному (до 20 - 30 %) снижению их несущей способности. Вот почему применяемые в настоящее время расчеты на прочность не вполне со-лветствуют действительным условиям работы конструкций и не могут гаранти-шть надежности их работы.

В данной части дипломного проекта изложены основные положения мето-щкидля расчёта секции крепи на примере линейной секции 1ОКП70. Несмотря к многообразие крепей, в большинстве случаев их перекрытия и основания вы-юлняются в виде пространственных листовых конструкций рамного типа и име-от одинаковый характер поломок и повреждений. Существующие методы расчета жтных крепей пригодны лишь для ориентировочных расчетов, так как они ба-ируются на применении общемашиностроительных методов расчета и не отра­жают влияния конструктивно-технологических факторов на несущую способ-гость конструкций.

В практике мирового крепестроения все больше применяются современ-ые научно обоснованные методы исследований и расчетов. В связи с этим при­едены основные положения метода конечных элементов (МКЭ) для расчета не-ущих элементов крепей и результаты математического моделирования на ЭВМ апряженно-деформированного состояния (НДС) металлоконструкций.

Применение МКЭ для расчета конструкций крепей дало возможность честь их пространственную многомерность, жесткость сопряженных элементов, еальные условия нагружения и приложения опорных реакций.

Метод конечных элементов (МКЭ) является мощным и надёжным средст-ом исследования поведения конструкций в условиях разнообразных воздейст-ий.

В настоящее время на рынке программного обеспечения имеется большое эличество комплексов МКЭ, в том числе АН8У8, МА8ТКАК, АВАдШ, СОЗ-Ю5 и др. Традиционно эти продукты относятся к категории САЕ (Сотрш.ег кЫ Еп§теегт§) программного обеспечения, применяемого при проектирова-ии конструкций. Эта категория программного обеспечения занимает прочное есто в списке САО/САМ/САЕ/018/РВМ, продуктами из которого том или ином аде пользуется большинство инженеров во всём мире.


Метод конечных элементов АЫ8У8 широко известен и пользуется попу­лярностью среди инженеров - исследователей, занимающихся вопросами дина­мики и прочности. Средства МКЭ АЫ5У8 позволяют проводить расчёты статиче­ского и динамического напряжённо-деформированного состояния конструкции (в том числе геометрически и физически нелинейных задач механики деформируе­мого твёрдого тела), форм и частот колебаний, анализа устойчивости конструк­ции, нелинейных переходных процессов и др.

2.2. Расчёт нагрузок действующих на секцию механизированной крепи оградительно-поддерживающего типа - ЮКП70

Механизированные крепи оградительно-поддерживающего типа предназначены для разработки пластов средней мощности и состоят, как правило, из одинаковых одностоечных секций, имеющих поддерживающую и оградительную части, среди которых преобладают оградительные элементы.

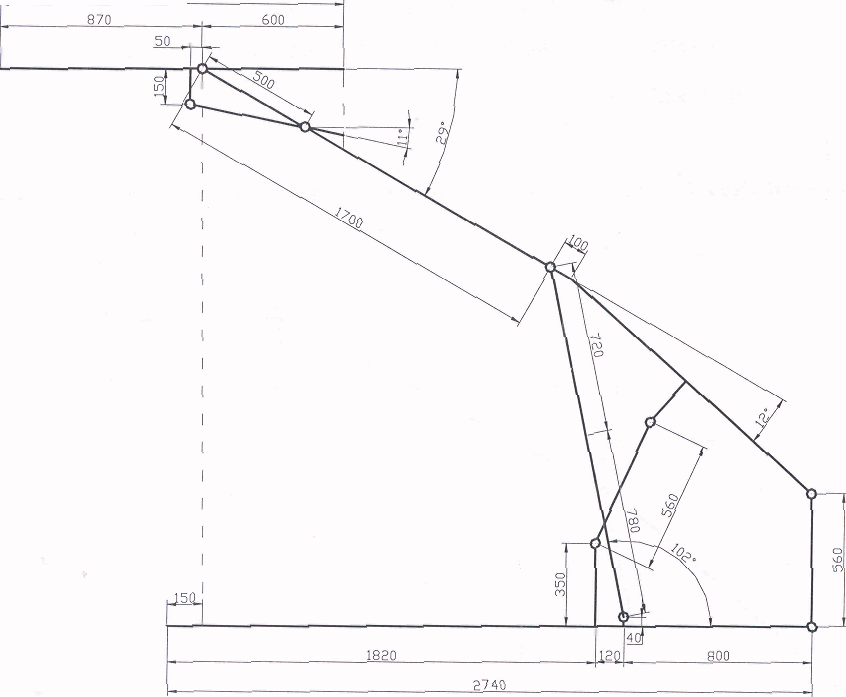
Рис. 2.2.1. Расчётная схема линейной секции крепи 1ОКП70 при полной раздвижности

_1470

2.2.1. Расчёт нагрузки на поддерживающий элемент секции крепи

Нагрузка на одноопорный поддерживающий элемент определяется как фоизведение расчётного удельного давления кровли на всю поддерживающую шощадь, включая площадь межсекционных зазоров и зазоров между передним онцом козырька и забоем.

1. Средняя нагрузка на поддерживающий элемент:


где:  ^^ = бООкН/м - удельное среднее давление на поддерживающий элемент в

соответствии с технической характеристикой; /г = 1,47м - длина поддерживающего элемента; $1 =0,3 - максимальный зазор между козырьком и грудью забоя; Ьп = 1м - ширина поддерживающего элемента;

52.п = 0,21 - максимальный зазор между поддерживающими элементами по ширине.

N3пк = 600 • (1,47 + 0,3) • 0 + 0,21) - 1285,02кЯ;

2. Несущая способность гидростойки (из технической характеристики):

2™х = 1900кЯ;

3. Максимальная нагрузка на поддерживающий элемент при полной раз-
движности секции:

-    вертикальнаяплос кость

АТ~ = СС* = ИГ - 5ша = 1900 • 5ш\02° - 1858,5кЯ; где: а = 102 - угол установки гидростойки при полной раздвижности секции.

-    горизонтальная плоскость

4. Максимальное давление на поддерживающий элемент:
™_            Л^я                                   1858,5


(* + $,)'№,+$2)     (1,47 + 0,3).(1-(-0,21)

Рис. 2.2.2. Схема действия нагрузки на поддерживающий элемент секции крепи

Мп™'= 1858,5кН Nп5^=

сГ"= 867,8кН/мг

= 1900кН

= 1858,БиН

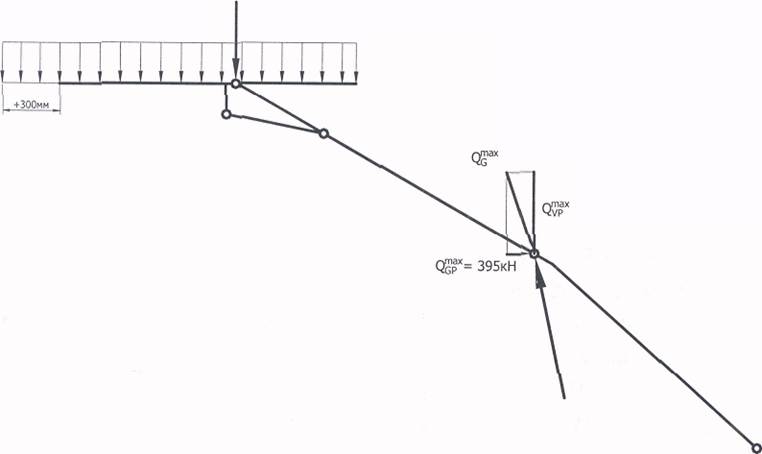Я5Г= 600«Н/мг

2.2.2. Расчёт нагрузки на оградительный элемент секции крепи

Нагрузка на оградительные элементы определяется отдельно для верти­кальной и горизонтальной составляющих как произведение расчётного удельного давления на площадь соответствующей проекции.

Если оградительный элемент представляет криволинейную поверхность, то последняя условно разбивается на участки. В данной конструкции секции можно выделить два участка.

Скачать файл