Испытания и события. Виды случайных событий и операции над событиями. Общие правила комбинаторики. Классическое определение вероятности. Примеры непосредственного вычисления вероятностей. Элементы теории корреляции

1.  Испытания и события. Виды случайных событий и операции над событиями.

Испытания – это опыт, эксперимент, наблюдение.

Например, подбрасывание игральной кости, монеты, выстрел из винтовки и.т.д.

Событие – это результат исход испытания.

Например, выпадение герба или решки.

Случайным событием называют любой исход опыта, который может произойти или не произойти, если будет осуществлена определенная совокупность условий.

Обозначаются события как А, В, С…

События прописываются:

А – выпадет 5 очков

В – выпадет 3 очка

Недостоверный исход элементарных событий обозначается через w.

Элементарные события рассматриваются, как неразложимые и взаимоисключаемые исходы опыта.

Множество всех элементов событий называется пространством элементов событий или пространством исходов и обозначается Ω.

Конечное пространство называется простым равновозможным исходом.

Событие будет называться подмножеством множества Ω.

Событие называется достоверным, если оно обязательно наступит в результате данного  опыта и обозначается через Ω.

Событие называется невозможным если оно заведомо не произойдет в результате опыта. Оно обозначается ø.

Два события называются несовместными, если появление одного из них исключает появление другого события в одном и том же опыте, т.е. не могут произойти в одном и том же опыте.

В противном случае события называются совместные, т.е. появление одного из них не исключает появление в одном и том же опыте.

События А1, А2, А3, … Аn называют попарно несовместными, если любые 2 из них не совместные.

Совокупность событий образуют полную группу, если они попарно несовместные и в результате каждого опыта происходит одно и только одно из них.

Событие называется равновозможное, если одно из них не является объективно более возможным, чем  другие, т.е. все события имеют равные шансы.

Два события называются противоположными, если в данном опыте они несовместимы и одно из них обязательно произойдет: А – появление герба, Ã – появление решки.

2.  Общие правила комбинаторики. Размещение, перестановки, сочетания с повторениями и без повторений.

Правило суммы:

Если некоторый объект А может быть выбран m способами, а некоторый объект В n, то либо объект А либо объект В может быть выбран m+n способами.

Правило произведений:

Если некоторый объект А может быть выбран m способами и после некоторого выбора объект В можно выбрать n способами, то пара объектов в указанном порядке можно выбрать m*n способами.

n - Количество всех вариантов

m – Количество благоприятных вариантов

Перестановка без повторений:

Перестановкой называются комиции, состоящие из одних и тех же n-различных элементов и отличает их порядком расположения.

Число всевозможных перестановок: Pn=n!

Размещение без повторений:

Размещением называют комбинацию, состоящую из n-различными элементами по m элементов, которые отличаются либо составом элементов, либо их порядком.

A^m_n =

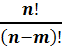
Сочетание без повторений:

Называется комбинация, состоящая из n-различных элементов по m, которая отличается хотя бы 1 элементом (порядок элементом не имеет значение)

С^m_n =

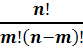
Размещение и сочетание с повторениями:

Если в размещение или сочетании из n элементов по m некоторые из элементов или все, могут оказаться одинаковыми, то такие размещение или сочетания называются с повторениями.

Размещение с повторениями (порядок важен)

Ã^m_n = n^m

Сочетание с повторениями (порядок не важен)

Č^m_n = С^m_n+m-1 =

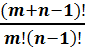
Перестановки с повторениями:

Если в перестановках из общего числа n-элементов есть k различных элементов, при этом, если первый элемент повторяется n1 раз, второй n2 раз, k повторяется nk раз. При чем n=сумме всех элементов, то такие перестановки называются с  повторением.

n=n1+n2+…+nk

Ã_n(n1,n2,…nk) =

3.  Классическое определение вероятности. Примеры непосредственного вычисления вероятностей.

Теория вероятности – это математическая наука изучающая закономерность, присущее массовым случайным явлениям.

В дискретном пространстве вероятность каждого элементарного исхода считается заданной и обозначается P(…)

Всегда вероятность события положительна, P=>0.

Сумма конечных или бесконечных вероятностей всех элементарных исходов – это элементарные события.

Вероятность события:

P(A)=

Вероятность события А называют относительные числа благоприятных данному событию (m) к числу всевозможных событий (n).

Свойства классической вероятности:

1)  Достоверные события равна

P(А)=1, n=m

2)  Вероятность невозможных событий

P(А)=P(ø)=0/n=0

m=0

3)  Вероятность случайных событий

P(A)=m/n

m<n 0<=P(A)<=1

Вероятность любого события удовлетворяет двойственному неравенству, которое находится в пределах от 0 до 1.

 Пример:

В урне находится 3 белых шара, 4 черных, 5 синих.

 Какова вероятность появления белого шара

n=3б+4ч+5с=12

A – Извлечение белого шара

P(A)=m/n=3/12

4.  Относительная частота. Устойчивость относительной частоты.