Вступ до курсу "Теоретичні основи електротехніки". Закони електромагнетизму. Основні поняття про електричні кола. Поняття про електричні схеми. Ідеальні елементи електричних схем заміщення, страница 5

Рис. 1.9

Співвідношення напруги і струму на R виражається законом Ома:

у загальному випадку для миттєвих значень (рис. 1.8, б):

u_R = Ri

у колах постійного струму (як частковий випадок попереднього):

U_R = RI

4. Ідеальний індуктивний елемент (рис. 1.10, а) відображає здатність реального об'єкта збуд­жувати магнітне поле в оточую­чому просторі при проходженні по ньому (об'єкту) електричного струму.

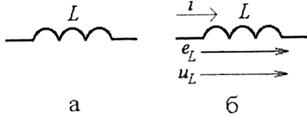
Рис. 1.10

Реальні об'єкти, які використовуються для отримання магніт­ного поля, - котушки індуктивності (рис. 1.11). Якщо у сфері поширення магнітного поля відсутні феромагнітні матеріали (немає феромагнітного осердя), то всі магнітні величини прямо пропорційні струму котушки.

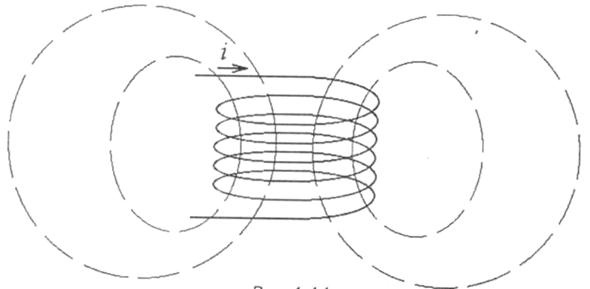
Рис. 1.11

Міра для ідеального індуктивного елемента - індуктивність L, що вимірюється в генрі [Гн] і вводиться як коефіцієнт пропорцій­ності у формулі:

ψ=L_i

де і - струм котушки або іншого об'єкта; ψ - її власне магнітне потокозчеплення (одиниця вимірювання - вебер [Вб]).

Наприклад, для котушки індуктивності (рис. 1.11), яка має кількість витків ω, магнітне потокозчеплення:

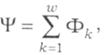
тобто дорівнює сумі магнітних потоків Ф_k, що пронизують окремі витки, причому ці потоки створені струмом і самої котушки.

Для практичної оцінки індуктивності є формула L ~ ω²S, де S - площа поверхні, що охоплюється витками котушки.

Якщо феромагнітні матеріали присутні, то прямої пропорції (1.6) між ψ та і немає, і коефіцієнт L має умовне призначення.

Співвідношення напруги і струму на ідеальному індуктивному елементі (рис. 1.10, б) утворюється наступним чином.

На підставі закону електромагнітної індукції ЕРС само­індукції:

 або,  з урахуванням, ;

Ця ЕРС створює напругу на індуктивному елементі ( рис. 1.10, б):

, або, враховуючи (1.8), .

У частковому випадку, в колі постійного струму при і=І маємо u_L =0. Тому в таких колах ідеальний елемент може не враховуватися (ділянка кола з L діє як простий провідник).

5. Ідеальний ємнісний елемент (рис. 1.12, а) відображає здат­ність реального об'єкта накопичувати електричний заряд і створю­вати в оточуючому просторі електричне поле.

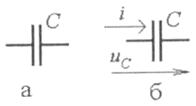
Рис. 1.12

Міра - ємність С, вимірюється в фара­дах [Ф] і вводиться як коефіцієнт пропорцій­ності у формулі q = Сu_с, де q - електричний заряд; u_с - напруга, що подається.

Реальний   об'єкт   для   накопичування електричних зарядів - це конденсатор. Для практичної оцінки
ємності конденсатора (рис. 1.13) є формула  де S і d - площа пластин і відстань між ними, відповідно.

Так як сила струму , то в ємнісному елементі, з урахуванням q = Сu_с:

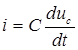
а з цього маємо загальне співвідношення напруги і струму на даному елементі (рис. 1.12, б):

У частковому випадку, в колі постійного струму всі напруги - постійні й на ємнісному елементі u_c = U_c. Тоді похідна за часом від постійної напруги дорівнює нулю. Отже, і сила струму в вітці, яка містить ємнісний елемент, також дорівнює нулю: i=0. Тому в таких колах ідеальний ємнісний еле­мент може не враховуватися, а ділянка кола із цим елементом розглядається як розрив елек­тричного кола.

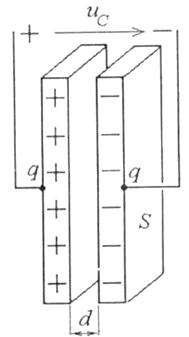
Рис. 1.13

6. Приклади електричних схем заміщення

Резистор і лампа розжарювання (рис. 1.14, а), конденсатор (рис. 1.14, б), котушка індуктивності (рис. 1.14, в) і джерела електро­енергії постійного струму (рис. 1.14, г) заміщуються так, як це пока­зано на рис. 1.14, а, б, в, г, відповідно. Це найбільш поширені, але не вичерпні варіанти схем заміщення поданих об'єктів. Так, наприклад, конденсатор С (рис. 1.14, б) при використанні в колі змінного струму низької частоти подається одним ідеальним ємнісним елементом С, а при високих частотах може бути використана сукупність ємніс­ного С і резистивного R ідеальних елементів. Крім того, одні і ті ж об'єкти по-різному заміщуються в залежності від того, в яких елект­ричних колах вони знаходяться - постійного або змінного струму.