Похибки засобів та результатів вимірювання. Визначення похибок при прямих вимірюваннях

Практичне заняття №4 (2 год)

Тема: Похибки засобів та результатів вимірювання

Завдання 3. Визначення похибок при прямих вимірюваннях.

Нехай нам необхідно виміряти деяку величину . При вимірюванні ми одержали значення Х_1,Х₂,Х₃,Х₄,Х₅…+Х_n. Середнє арифметичне значення з цих результатів, тобто

                                        Х=(Х1+Х2…+Хn)/n=1/n∑Xі                          (2.1)

є величина, найбільш близька до істинного значення (дійсного значення).Ця величина називається середнім значенням вимірюваної величини.

Звідси випливає, що кожне вимірювання повинне бути повторене декілька разів.

Визначимо різниці між середнім значенням вимірюваної величини і значеннями Х₁, Х₂, Х₃, ... Хn, одержаними при окремих вимірюваннях:

Х-Х1=ΔХ1

Х-Х2=ΔХ2

Х-Х3=ΔХ3

¯¯¯¯¯¯¯¯¯

Х-Хn=ΔХn                                            ( 2.2)

Одержані величини називаються абсолютними похибками і можуть бути додатними і від'ємними.

Для визначення середньої абсолютної похибки результату беруть середнє арифметичне абсолютних значень (модулів) окремих похибок:

                                      ΔХ=( |Х1|+|Х2|+…+|Хn| )/n=1/n∑|ΔXі|                  (2.3)

            Відношення середньої ΔХ1/Х, ΔX2/Х…ΔXn/Х  називаються відносними

похибками окремих вимірювань.

Відношення середньої абсолютної похибки результату ΔX до його середнього значення х називається середньою відносною похибкою результату вимірювань

δ=ΔΧ/Χ.

Відносні похибки прийнято виражати у відсотках

                                              δ=ΔΧ/Χ*100%                                   (2.4)

Істинне (дійсне) значення величини, яка вимірювалася

                                х_д= х + Δх(2.5)

З вищенаведеної формули випливає, що дійсне знамення вимірюваної величини знаходиться в інтервалі

                                                                        х-Δх≤ хδ≤х +Δх                       (2.6)

Теорія ймовірностей дає більш точну формулу для розрахунку похибки результату

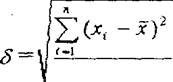
де δ- середньоквадратичне відхилення;

X5 - результат і-того вимірювання;

n -кількість вимірювань;

х - середнє значення вимірюваної величини. В цьому випадку остаточне значення вимірюваної величини

                                                              X_ġ=X±δ                                                              (2.8)

Приклад 1. При вимірюванні довжини були одержані такі результати (мм): 154,0; 153,5; 153,5; 154,5; 154,0. Визначити абсолютну та відносну похибки результату та встановити межі , в яких знаходиться величина вимірюваної довжини 1

1. Визначимо середнє (дійсне) значення довжини. З формули (5) маємо:

Х=154,0 + 153,5 + 153,5+154,5 + +154/5 = 153,9(мм)

2. Визначимо абсолютні похибки окремих результатів вимірювання. З формули
(6) маємо:

153,9-154,0 = -0,1

 153,9-153,5= 0,4

153,9- 153,5= 0,4

153,9- 154,5 =-0,6

153,9- 154,0 = -0,1

3.  Визначимо середню абсолютну похибку результату (формула 7).

ΔХ = |-0,1|+|0,4|+|0,4|+|-0,6|+|-0,1| / 5=0,32(мм)

Отже, величина вимірюваної довжини находиться в межах

153,58 ≤l≤ 154,22

4. Визначимо відносну похибку результату (формула 2,4).

δ= 0,32/153,9* 100% = 0,2%

Розрахунок абсолютної похибки за формулою (2.7) дає значення

δ= 0,37 мм.

Це уточнене значення можна прийняти, як остаточне. З урахуванням цього

1 = (153,9 ± 0,37) мм,     δ= 0,24%.

Звичайно у випадках, коли не співпадають величини Ах, розраховані за формулами (7) і (11), завжди беруть більшу величину.

Приклад 2. Гри визначенні жирності коров'ячого молока були одержані такі результати (у відсотках): 2,20; 2,40; 2,25; 2,50; 2,30; 2,40; 2,70. Визначити абсолютну та відносну похибки та записати остаточний результат вимірювання.

1. Якщо розмістити результати визначення у порядку зростання, ми
побачимо, що останній результат є промахом: 2,20; 2,40; 2,25; 2,50; 2,30; 2,40;
2,70. Середнє значення навіть з врахуванням останнього результату дорівнює

х = 2,4.

Абсолютна похибка останнього результату Δх₇ =-0,35, тобто на 0,15 перевищує абсолютну   похибку   першого   вимірювання.    Тому   останній   результат відкидаємо.

   2.      Визначимо середнє (дійсне) значення величини жирності молока

Х=14,05/0,6=2,34%

   3.      Визначимо середню абсолютну похибку результату:

ΔХ=0,55/6=0,092

4. Визначимо відносну похибку результату:

δ=0,092/2,34*100%=3,9%

5. Для порівняння визначимо абсолютну похибку за уточненою формулою (2.7):

δ=0,1%

1.  Остаточний результат (2,34 ± 0,1%).

КОНТРОЛЬНІ ПИТАННЯ

1.  Які існують похибки результатів вимірювання?

2.  Що називають прямими вимірюваннями? Непрямими вимірюваннями?

3.  Як визначають абсолютну та відносну похибки при прямих вимірювання?

4.  Як визначають абсолютну та відносну похибки при прямих вимірюваннях?