Сцинтилляционные детекторы, страница 5

,где   D_p –дисперсия вероятности p того, что фотон, образованный в сцинтилляторе, приведёт к появлению электрона на первом диноде ФЭУ (это произведение вероятности фотона попасть на фотокатод на вероятность фотоэффекта на фотокатоде, на вероятность попадания электрона на первый динод), N -среднее число фотонов испущенных сцинтиллятором, σ -средний коэффициент вторичной электронной эмиссии первого динода.

Первый член этого выражения обратно пропорционален числу фотонов, возникающих в сцинтилляторе, то есть энергии излучения.

Величину сложно рассчитать, её можно измерить для каждого конкретного сцинтиляционного счётчика..

 Таким образом, относительная величина дисперсии распределения амплитуд импульсов можно представить в виде трёх членов. Первый зависит от числа фотонов в сцинтилляторе,  то есть от энергии излучения, а второй определяется флуктуациями в конверсионной эффективности фотокатода, флуктуациями  вероятности попадания фотонов на фотокатод, флуктуациями вероятности сбора электронов на первый динод.

 Второй коэффициент зависит от качества изготовления фотоумножителя: одинаковости  конверсионной эффективности фотокатода в различных точках, эффективности сбора электронов на первый динод, качества соединения сцинтиллятора с фотоумножителем, равномерность отражателя и т.д. Этот коэффициент не зависит от энергии регистрируемого излучения.

Третий член определяющий дисперсию коэффициента умножения. Дисперсия коэффициента усиления обратно пропорциональна числу электронов пропадающих на первый динод, и не зависит от числа динодов в умножителе.

Распределение амплитуд импульсов около своего среднего значения хорошо аппроксимируется распределением Гаусса. Пологая что энергия кванта и амплитуда импульса пропорциональны, и учитывая энергию, затрачиваемую на создание одного фотона в сцинтилляторе, получим для энергетического разрешения счётчика выражение:

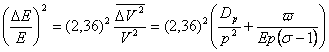, где ω-энергия затрачиваемая на создание одного фотона сцинтиллятора.

Энергетическое разрешение сцинтилляционных счётчиков оказывается не очень высоким. Например для ΝaI (Tl) для создания одного фотона затрачивается около 40 эВ, вероятность р составляет около 5% ( конверсионная эффективность фотокатода не лучше 10%; потери света; потери электронов при сборе на первый динод), коэффициент вторичной эмиссии около 3, второй коэффициент в выражении будет равен .Первый коэффициент для очень хороших счётчиков составит 2.10 ^–4 .

Так как световой выход низок,  в среднем требуется около 200-1000эВ для получения фотона, энергетическое разрешение счётчика невысокое, конверсионная эффективность сцинтиллятора очень мала. Свет испускается во всех направлениях и частично поглощается самим сцинтиллятором. Для увеличения светосбора поверхность кристалла обращённая к входному окну матируется.

Для сцинтилляционного счётчика множитель Фано равен 1.

Энергетическое разрешение сцинтилляционного спектрометра можно записать в следующем виде:

R(%)=100(90/sE+0,0033/E½),

где Е-энергия рентгеновских фотонов, кэВ;

s-интегральная чувствительность фотокатода, мка/лм.

Газовые пропорциональные сцинтилляционные детекторы( gasproportionalscintillationcounter(GPSC))

Наличие  флюктуаций газового усиления газового усиления, как показано выше ,ухудшает энергетическое разрешение пропорционального детектора практически в два раза.. Если поле таково, что достигается лишь возбуждение атомов газа наполнителя с последующей регистрацией света, возникающего при возвращении атомов в не возбуждённое состояние, то мы имеем дело с новым видом газоразрядного детектора газовым ,пропорциональным, сцинтилляционным детектором (ГПСС).