Собственные колебания оптического резонатора

5. СОБСТВЕННЫЕ КОЛЕБАНИЯ ОПТИЧЕСКОГО РЕЗОНАТОРА

          Собственные колебания, или моды, которые могут возникать в ОР, делятся на два типа. Продольные (осевые) колебания формируются за счет излучения, распространяющегося строго вдоль оси ОР. Поперечные (внеосевые или угловые) колебания формируются потоками квантов, распространяющихся под малыми, порядка 10^–4…10^–3 рад, углами к оси ОР.

5.1. Продольные моды

          Простейший оптический резонатор состоит из двух отражающих поверхностей – зеркал. Требования к зеркалам, свойства их подложек и отражающих покрытий, а также виды потерь излучения в ОР рассмотрены в [1]. В ОР возможно распространение двух встречных волновых потоков, которые формируются приосевой частью потока квантов и распространяются параллельно оси резонатора. В ОР будут иметь преимущества те продольные колебания, которые испытывают минимум потерь при отражении от зеркал. Минимальными потерями, а следовательно, и максимальным усилением будут обладать те колебания, для которых выполняются нулевые граничные условия: напряженность Е электрического поля на зеркалах равна нулю. Тогда в плоскости зеркал З₁, З₂ фазы оптических волн φ = kπ , где k = 0, 1, 2…, а E_1,2 = 0. Соответственно, плотность мощности потерь I_α = α_потI_λ → 0, где α_пот – коэффициент потерь; I_λ ~ E² – плотность потока квантов, падающего на зеркало.

          Продольные колебания являются суперпозицией встречных волн, распространяющихся в ОР вдоль оси z. Нулевые граничные условия означают, что на оптической длине nL резонатора должно укладываться целое число полуволн λ/2. Процесс взаимодействия разнонаправленных волн с одинаковой частотой  сопровождается появлением в пространстве пучностей и узлов энергии – стоячих волн. Условие образования стоячих волн записывается как  

где n – показатель преломления среды, заполняющей ОР (для газовых активных сред п = 1); L – геометрическая длина ОР; q = 1, 2, 3 ... – целое число, имеющее в оптическом диапазоне порядок 10⁴...10⁶.

          Колебания с длинами волн ν_q, соответствующие тому или иному значению числа q, являются резонансными. Они формируют спектр собственных частот оптического резонатора, называемых продольными или осевыми модами.

          С учетом (5.1) частота продольной моды с произвольным продольным индексом q определяется как

Из (5.2) следует, что любые две соседние резонансные частоты с индексами (q + 1) и q располагаются на оси частот через равные интервалы Δν_q:

Каждая резонансная линия имеет конечную ширину Δν_ОР, определяемую уровнем  потерь  излучения  или, иными словами, добротностью ОР (рис. 5.1).

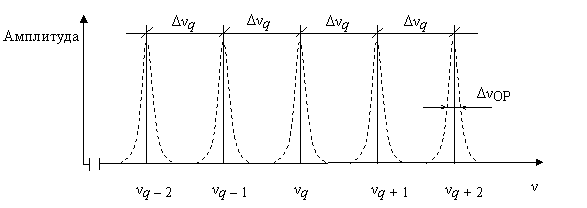
Рис. 5.1. Частотная характеристика ОР.

          Из (5.3) следует, что межмодовые интервалы Δν_q ≠ f(q) между соседними резонансными частотами не зависят от значений индекса q –  являются инвариантом по отношению к индексу.