Теоретические основы определения места судна по звездам. Теоретические основы определения широты по меридиональной высоте Солнца и Полярной звезде, страница 2

Выбор вероятнейшего обсервованного места При двух линиях место прини­мается в пересечении линий, а его точ­ность оценивается построением эллип­са ошибок [формулы (260)]. При трех линиях, полученных по светилам в раз­ных частях горизонта, вероятнейшее место принимается в середине треуголь­ника по методу весов (M1). При свети­лах в одной части горизонта получается два места: M1 и M2 (по методу биссект­рис); за обсервованное принимаем то из них которое ближе к опасности. Веро­ятнейшее место в этом случае опреде­ляется по обобщенному методу наимень­ших квадратов, как показано выше. При четырех линиях место лучше всего выбирать по методу весов — в середине фигуры погрешностей. Оценка точности при трех и четырех линиях производится построением круга ошибок по формулам (251) — (253) с удвоением М, что дает вероятность около 95 %. Если получены две обсервации, то после графического приведения к одному зениту они осредняются по методу весов.

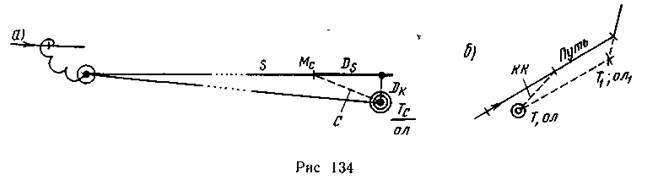
Использование полученной информа­ции для навигации. Каждая обсервация должна сопровождаться анализом счис­ления. По направлению от счислимого места на обсервованное определяется невязка С (например, на рис. 134 С  = 115°— 8,0'), и далее обсервация анализируется.

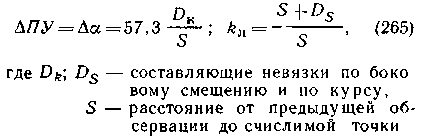
Ошибки в пути ∆ПУ и в учете рас­стояния (коэффициенте лага) опреде­ляются по приближенным формулам:

Величины   ∆α ± 1-1,5°   и    коэффи­циент лага от 0,98 до 1,02 можно считать следствием обычных случайных ошибок счисления. Если же они превышают эти величины, то отклонения следует от­нести к систематическим ошибкам в поправках приборов или принятом те­чении. Особенно полезен анализ после­довательных обсерваций — через 6— 12Ч, например в вечерние и утренние сумерки и т. д. Если снос получается в одном направлении и возрастает, то это показывает, что в обсервациях нет про­махов и что действует постоянная при­чина сноса. Анализ позволяет штурма­ну судить о работе приборов, устойчи­вости их поправок и правильности учета течения и дрейфа.

Перенос счисления в обсервацию.  В результате анализа принимается реше­ние о переносе счисления в обсервованное место. Как правило, обсервация по двум и трем звездам недостаточно надеж­на для переноса счисления; если же привлекался второй наблюдатель или обсервация выполнена по четырем звез­дам, то после анализа переносить счис­ление можно с учетом обстоятельств плавания. Перенос счисления сопровож­дается определенными действиями: либо изменением курса для выхода на путь, намеченный предварительной проклад­кой (рис. 134, б), либо изменением вре­мени плавания до поворота на следую­щий путь. Соответствующие расчеты КК или Т1 и ол1 производятся по дан­ным с карты.

Теоретические основы определения широты по меридиональной высоте  Солнца и Полярной звезде.

Раздельное получение координат φ и δ места наблюдателя по высотам све­тил с достаточной точностью возможно только в частных положениях светила (см § 65) Широту следует определять по светилу на меридиане (А = 180°, 0°), а долготу — по светилу на первом верти­кале (А = 90°, 270°) До открытия ме­тода высотных линий координаты места в море определялись раздельно. В на­стоящее время значение аналитических приемов определения координат умень­шилось, но в силу традиций и вследствие простоты обработки наблюдений сохра­нилось несколько способов получения широты места в море

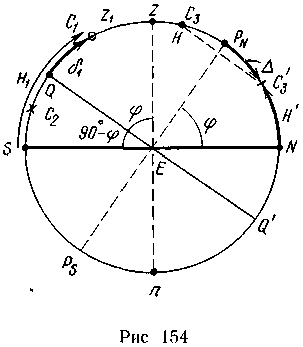Определение широты по меридио­нальной высоте светила.
Если светило находится в верхней кульминации (рис 154), то его высота является мери­диональной H, азимут А = 180°(0°), tм = 0° Уравнение круга равных высот (209), т е формула sin h, примет вид

sinH = sinφsinδ + cosφcosδcos0°

или

sinH = cos(φ-δ)

Так  как   H = 90  — Z,  то   sinH= cosZ = cos (φ -δ)   и  для   аргумен­тов  в первой  четверти

Z = φ—δ,

откуда                                            

φ = Z+δ

Эта формула  применяется для опре­деления φ в момент верхней кульмина­ции  светила, причем δ имеет знак «+» при  одноименных  φ  и δ  и  знак «—» — при  разноименных

Напомним, что наименование Z об­ратно H, а H одноименно с точкой гори­зонта (N или S), над которой измеряет­ся высота Наименование широты полу­чается одинаковым с наименованием большего члена формулы В общем виде получим

    φ = Z ± δ                   (284)

Формулу (284) для разных положе­ний светил можно получить и по сфере (см рис 154) Для светила С1, у кото­рого δ одноименно с φ, имеем

Z1 = 90 – H1           φ = Z1+δ1

Для светила С2, у которого δ разно­именно с φ, имеем

φ = Z2-δ2

Для светила Сз, у которого δ одно­именно с φ и больше ее имеем

φ = δ3-Z3

Для нижней кульминации светила С'3 получим

φ = H’ + ∆                    (285)

где ∆ — полярное   расстояние  светила,    рав­ное  90-δ

Практически метод определения φ по Н применяется теперь только к Солн­цу В формулах (284) и (285) применя­ется высота светила Н на меридиане наблюдателя

Определение широты судна по высоте полярной звезды.

Высота полюса мира над горизонтом равна широте места, поэтому если бы в каждом из полюсов мира находилось по звезде, то стоило бы только измерить высоту такой звезды и исправить ее по­правками, чтобы получить широту места

В самих полюсах звезд нет, но неда­леко от северного полюса находится довольно яркая звезда α Малой Медве­дицы, называемая за свое близкое рас положение к полюсу Полярной звездой Для Полярной на
1985 г ∆ = 48', поэ­тому суточным движением она описы­вает параллель со сферическим радиу­сом меньше 1° (рис 156) Вследствие этого азимут Полярной всегда близок к 0° (см § 61) и она расположена всегда в выгодных условиях для определения φ По этой же причине высота Полярной всегда близка к широте и может отли­чаться от последней лишь на небольшую величину х Задача определения φ по высоте Полярной сводится к нахожде­нию этой поправки х, равной разности между высотой Полярной в данный мо­мент и широтой места

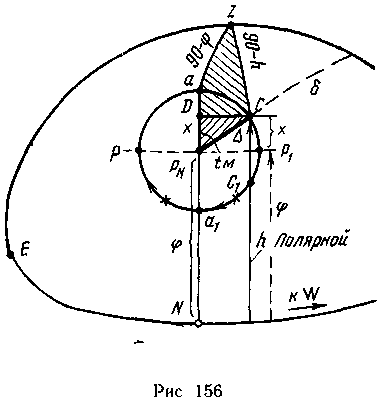В точке а параллели х = —∆, в про­тивоположной точке а1х = +∆, в точ­ках р и р1 лежащих на альмукантарате полюса, х = 0 Из рис 156 видно, что для промежуточных точек С или С1 получим

 

Из треугольника PNDC, принятого за плоский получим приближенно

Чтобы получить знак х, в эту формулу вводим «—» и заменяем tм по формуле (71), т е Получим

Точную формулу для х, учитываю­щую сферичность треугольника, при­водим без вывода

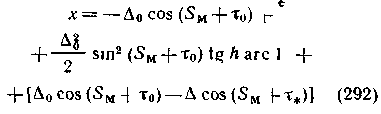
Значения т и ∆ Полярной довольно быстро изменяются, поэтому таблицы для х помещены в МАЕ

По этой формуле, в которой ∆0 и т0 среднегодовые значения координат По­лярной, в МАЕ на каждый год со­ставлена таблица, озаглавленная «Широ­та по высоте Полярной» (табл I—III, с 277—280) Первая основная поправка I приводится по аргументу Sм, данному через 30', поправка II за сферичность треугольника приводится по h и Sм, из­менение поправки в течение года учиты­вается в поправке III, приводимой в МАЕ по Sм и дате Широта получится добав­лением к высоте этих поправок с их знаками

До  широт 50    параллель  φ0  можно принимать  за  линию   положения

Определение φ по Полярной можно выполнять в северных широтах от 5 до 70 в сумерки и ночью при видимом го­ризонте Однако при наличии более ярких звезд, видимых над более четким горизонтом, следует предпочесть обычный способ высотных линий Действие оши­бок наблюдений на параллель φ0, или линию положения, аналогично рассмотренному выше для высотной линии, т е действительная параллель находится внутри полосы шириной ±mφ

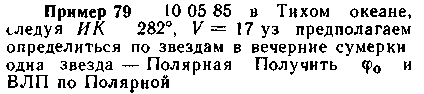
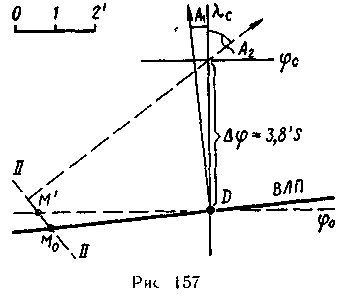
Нанесение    ВЛП   по   найденной   φ0.

Параллель φ0 не является линией поло­жения (не круг равных высот). Для по­лучения ВЛП следует: по меридиану λс (рис 157) отложить ∆φ, в полученной точке D проложить линию азимута А1 перпендикулярно ей в точке D провести ВЛП Если имелась вторая ВЛП, то получим место М0 (но не М') В про­шлом широко применялись определения по Солнцу: «утро—полдень» (ВЛП — φ0) и «полдень—вечер» (φ0 — ВЛП), одна­ко они не полностью отвечают выгодным условиям.