Интерферометр состоит (см. рис.2.25 в [1]) из 1) двух разнесенных на отрезок (базу, длиной l около метра, т.е. пяти длин волн и более) приемных антенн, 2) двух линейных приемных ВЧ трактов (сдвиг фазы в которых может отличаться на DY) и 3) измерителя фазы, выдающего отсчет Ykизм. Для упрощения выкладок полагаем, что отсчет фазы ведется в долях и целых числах единиц циклов (этой единице обычно сопоставляют 2p радиан или 360О). Тогда полная разность фаз Yk наведенных в антеннах сигналов должна выражаться как частное от деления на длину волны разности расстояний Drk от k-го ИСЗ до разнесенных антенн, т.е. Yk=Drk/l. Отсчет Ykизм фазометра должен содержать неизвестную неизменную (независящую от номера ИСЗ) составляющую - линейный элвивалент d=lDY погрешности из-за неидентичности приемников, т.е. Ykизм=Yk+DY=[(Drk+d)/l).
5.2.2. Поскольку расстояния до ИСЗ на несколько порядков превышают базу, то прямые, соединяющие приемные антенны и ИСЗ, допустимо считать параллельными одному орту радиуса-вектора ИСЗ
rk0=Rk/Rk=x0cxk+y0cyk+z0czk, (5.3)
исходящему из общей приемной антенны для двух интерферометров. Полагаем, что длины баз одинаковы и равны l, причем база одного из интерферометров совпадает с ортом в продольной оси судна, другого – с ортом а поперечной оси. Очевидно, что истинные разности расстояний Drkb и Drka равны проекциям баз на орт ИСЗ, т.е. длине I базы, умноженной на скалярное произведение орта базы на орт ИСЗ:
Drkb=lbrk0=(cbxcxk+cbycyk+cbzczk)l, Drka=lark0=(caxcxk+caycyk+cazczk)l.
34
Заметим, что эти разности могут быть и отрицательными и положительными, т.е. -l< Drk <l, Разделив все члены равенства на длину волны можно заключить, что количество целых циклов в полной разности фаз может принимать значения от –l/l до + l/l. Полагаем, что целоцикловая однозначность фазовых измерений обеспечена одним из известных методов, освещенных в соответствующей литературе.
Измеренные разности дальностей c учетом неидентичности двух РПК
Drkbизм=(cbxcxk+cbycyk+cbzczk)l +db, Drkaизм=(caxcxk+caycyk+cazczk)l + da (5.4)
после деления на длину базы и с использованием обозначений
pbk=Drkbизм/ l, pak=Drkaизм/ l, db=db/ l, da=da/l. (5.5)
целесообразно переписать в более компактном виде:
cbxcxk+cbycyk+cbzczk+db=pbk, caxcxk+caycyk+cazczk+da=pak. (5.6)
Ансамбль равенств при k=1,2,3 ...- это система линейных уравнений, из которых должны определяться оценки искомых направляющихе косинусов баз интерферометров. Ясно, что среднеквадратическое отклонение СКО погрешностей этих оценок будет линейно зависеть от СКО sp нормированной величины p =Dr/ l из (5.5)
5.3. Алгоритмы и погрешности определения истинного курса,
крена и дифферента по сигналам 4-х ИСЗ.
5.3.1. Ограничимся рассмотрением случая 4-х ИСЗ, когда k=1.2.3.4 и систему линейных уравнений (5.6) можно представить с помощью апробированных в п.3 и п.4 матриц
; 
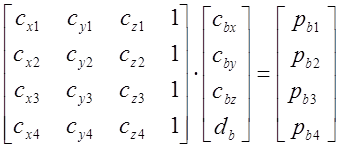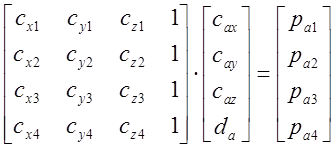. (5.7)
Необходимые нам направляющие косинусы определяются по формулам п.3 (с соответствующей заменой обозначений)
,
,
,
,
позволяя найти углы И,К,Д по формулам (5.2).
5.3.2. Средние квадратические погрешности определения направляющих косинусов при одинаковых СКП sp величин pak и pbk нормированных по (5.5) разностей расстояний (5.4) выражаются аналогично (3.6):
35
;
(5.8)
. (5.9)
.
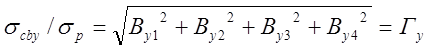(5.10)
Связь погрешности истинного курса DИ, дифферента DД и крена DК (в радианах) с погрешностями направляющих косинусов вытекает, если взять дифференциал соответствующего равенства из (5.1) или (5.2) и заменить знак дифференциала на приращение.
Получаем DК=Dсaz/cosK, DД=Dcbz/cosД. Такая же взаимосвязь сохранится и для среднеквадратических погрешностей СКО, т.е. sК=scaz/cosK, sД=sсbz/cosД, что с учетом (5.8) позволяет получить расчетные соотношения
sК=spГz/cosK, sД=spГz/cosД (5.11)
Оценку погрешностей истинного курса получим, приведя дифференциал истинного курса И=arctg(сbх/сby) к приближению DИ @ сbyDсbх-сbxDсby. Поэтому СКО погрешности с учетом (5.9), (5.10) и (3.7) можно выразить как
sИ=spГм, (5.12)
где Гм=(Гх2+Гу2)½.
При интерферометоических измерениях - из-за небольшого разноса антенн - влияние нешумовых источников погрешностей (перечисленных в п.1.3.2) не должно сказываться. Влияние шумов можно оценить по полученному с помощью (1.13) и (1.15) соотношению для среднеквадратической погрешности srш нормированной величины p =Dr/ l из (5.5):
spш»(0,0428/l)[Пссн(N0/Р)]0,5(рад.)=(2,452/l)[Пссн(N0/Р)]0,5(град.). (5.13)
5.4. Понятие о методах исключения многозначности
фазовых отсчетов интерферометра.
В п.5.2.2 установлено, что количество целых циклов в полной разности фаз может принимать значения от –l/l до + l/l. Если база l=1м, то измеренному (однозначно в пределах лишь одного цикла) фазовому отсчету Yk следует добавить одно из одиннадцати (от –5 до +5) целых циклов.
5.4.1. Известный радиотехнический метод исключения рассматриваемой многозначности одного интерферометра базируется на использовании одинаково направленных баз различной длины, например, l1 <l2 <l3 =1. Причем наименьшая длина lmin=l1 должна быть меньше 0,5l, что обеспечивает однозначный отсчет Yk1, такой, что –0/5< Yk1<+0,5., то. После умножения измеренного однозначного отсчета на отношение баз l3/l1 получилась бы величина (l3/l1)Yk1 , целочисленная часть которой (при малых инструментальных погрешностях измерений) определила бы неизвестное целое число циклов в отсчете Yk3 интерферометра с метровой базой l3, Учет реальных погрешностей заставляет в нашем примере использовать еще одну базу l2 .
36
Этот метод в СРНС неприемлем из-за трудностей исключения инструментальных погрешностей измерений при минимальной базе, размеры которой (lmin=l1=0,5l<10 см) соизмеримы с размерами приемных антенн круговой поляризации.
5.4.2. Второй метод, исследованный в /17/ и реализуемый в некоторых разработках, состоит в сопоставлении оценок истинного курса получаемых с помощью 1) интерферометров и 1) автономного (например, гироскопического) указателя курса и 2) интерферометров при всевозможных комбинациях целых чисел циклов. Наиболее правдоподобная комбинация этих чисел будет соответствовать минимуму разности указанных оценок.
5.4.3. Принцип реализованного в зарубежной аппаратуре одного из способов базируется на использовании метода наименьших квадратов МНК к уравнениям (5.7), которые будучи составленными не для четырех, а для всех n видимых ИСЗ, могут быть приведены к виду (3.9) с составлением квадратичного функционала (3.10), зависящего от выбора значений целых чисел циклов. Этот функционал (сумма L квадратов погрешностей) будет иметь минимальное значение лишь при условии, что в фазовые отсчеты, полученные по каждому ИСЗ, подставлено истинное число целых циклов. Истинный набор целых чисел циклов находится, по существу, методом перебора громадного количества (2l/l+1)n возможных наборов с использованием приемов, сокращающих время перебора.
5.4.4. Результаты анализа подобных предыдущему способов позволили в /10 / предложить оригинальный способ без использования громоздких алгоритмов и процедур МНК. Здесь на основании выявленного свойства (теоремы) отсчетов интерферометра по сигналам четырех ИСЗ здесь удалось построить процедуру поиска истинного набора целых чисел циклов путем отбрасывания тех комбинаций из троек и четверок целых чисел, которые не удовлетворяют установленным условиям для трад (троек) ИСЗ и тетрад (четверок) ИСЗ. При этом скорость и надежность поиска истинного набора увеличиваются по сравнению с известными зарубежными аналогами.
5.4.5. Более тщательное и глубокое рассмотрение методов обеспечения однозначности интерферометрических измерений может быть получено при выполнении соответствующих исследовательских дипломных и аспирантских работ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.