Предвычисление орбитальных параметров искусственного спутника Земли, страница 2

E-esinE=M.                                                            (2.7)

Решается (2.7) методом последовательных приближений.

Для определения  истинной аномалии используются  получаемые из треугольника ОКН соотношения

ОН=aсosE=(a²-b²)^0,5+rсosq и НК=asinE=(a/b)rsinq, которые приводят после громоздких выкладок к простым формулам;

sinq=(cosE-e)/(1-ecosE),    сosq=[(1-e²)^0,5sinE]/(1-ecosE).           (2.8) 

Радиальная v_r=dr/dt и тангенциальная v_t=rdq/dt составляющие скорости ИСЗ  находятся c помощью (2.4) и (2.5) в виде 

v_r=(ma/b²)^0/5esinq, v_t=(ma/b²)^0/5(1+ecosq).                                             (2.9)

18 

2.3. Принципы определение положения ИСЗ  в пространстве

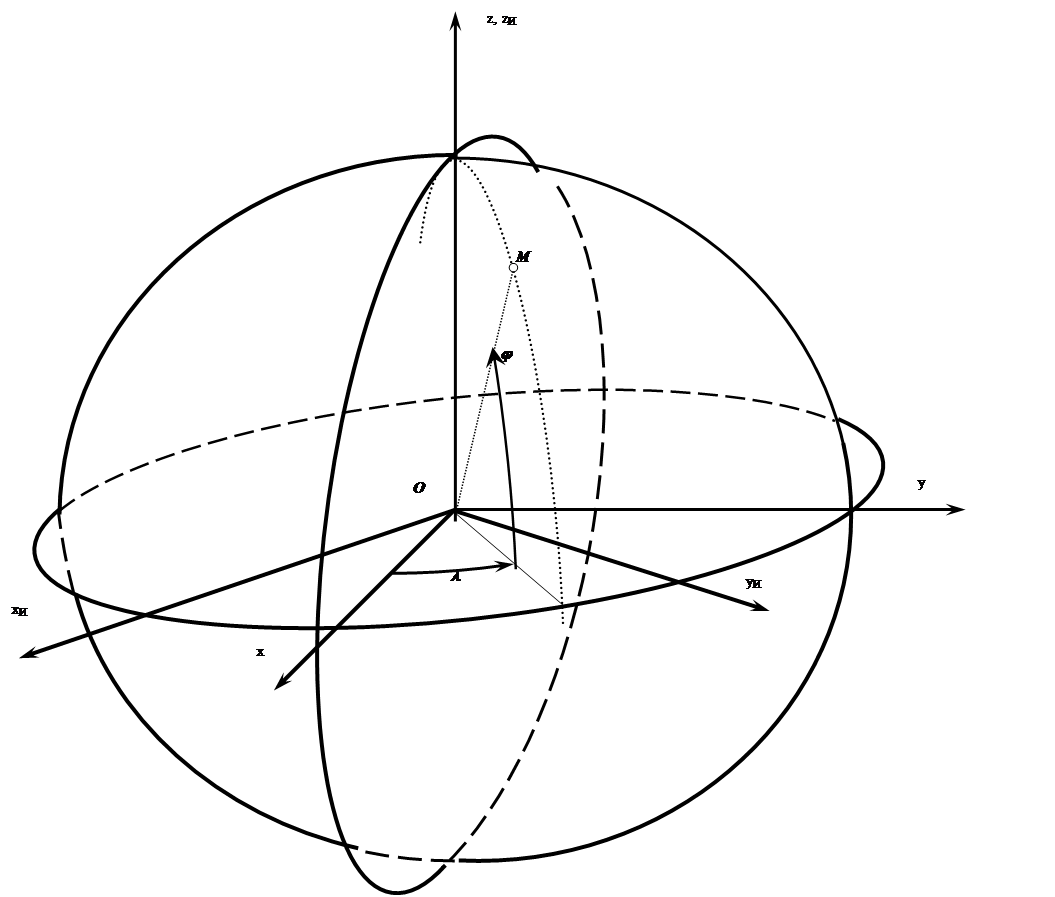
2.3.1.В ряду используемых в CРНС систем координат наиболее важны две декартовые геоцентрические (с началом в центре Земли): инерциальная {x_И, y_И, z_И}  и гринвичская {x, y, z} с  общей  осью  аппликат - осью вращения Земли, направленной в полюс мира вблизи Полярной звезды. С этой  осью и совмещены  оси z_Ии z (см.  рис. 2.4). Плоскости  x_и0y_и и x0y совмещены с экваториальной плоскостью, которую орбита ИСЗ пересекает в двух точках, называемых: 1) восходящий узел и 2) нисходящий узел. Ось абсцисс x_и инерциальной (неподвижной) системы координат направлена на созвездие Овна и параллельна прямой, соединяющей центры  Земли  и Солнца в момент весеннего равноденствия (равной освещенности Северного и Южного полюсов Земли). Оси x,y гринвичской системы вращаются вместе с Землей. В момент равноденствия и далее через каждые сутки оси абсцисс х и у оказываются  совмещенными.

			и
		Рис. 2.4.    Системы  координат  в  спутниковых  РНС

 

19

Для рассмотрения некоторых (например, точностных) характеристик СРНС удобна горизонтная  система  координат, в которой начало координат располагается в известной (или счислимой) точке, ось у обычно совмещается с линией меридиана и направлена на Север, а ось х - на  Восток (см.  рис. 2.5). Угловую ориентацию радиуса-вектора из начальной точки на ИСЗ определяют азимутом и углом возвышения. Максимальный угол возвышения над горизонтом называется кульминацией. Иногда ось горизонтной системы задается по маршруту движения судна.

20

В судовождении находят применение и географические координаты (широта и долгота).        

Следует заметить, что перевод аналитических выражений координат ИСЗ  из одной системы координат в другую выполняется с использованием известных из аналитической геометрии формул преобразования координат в матричной форме, реализуемых в алгоритмах микропроцессоров судовой аппаратуры без затруднений. Поэтому далее выбор вида координатной системы будет обуславливаться лишь  критериями удобства пользования и компактности изложения.

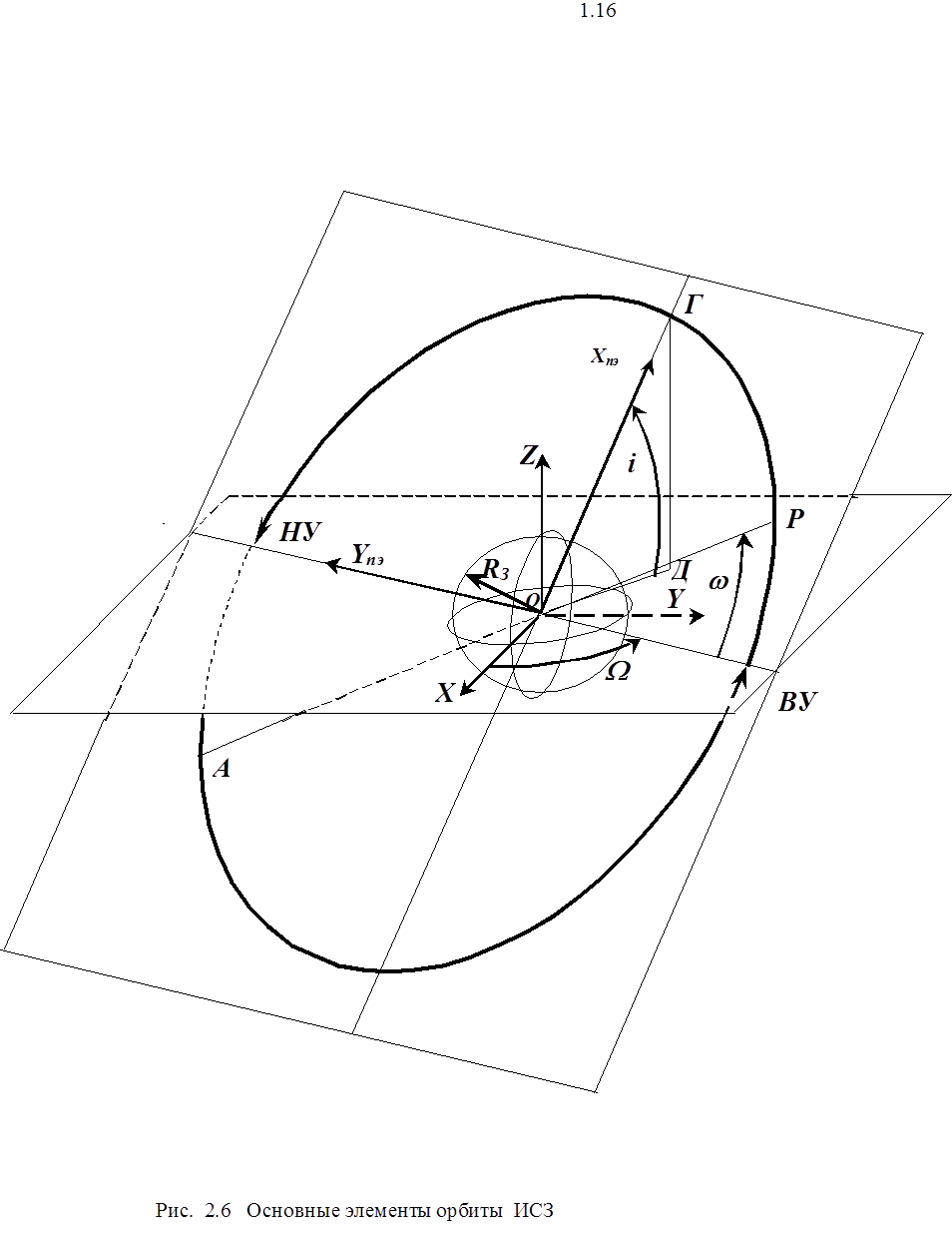
2.3.2. Формулы п. 2.2 определяют только на плоскости орбиты текущие координаты ИСЗ (соответствующие моменту времени t) при трех известных параметрах a,  e  и t_П. Для определения координат в пространстве необходимо знать еще три параметра. Обычно для геоцентрических систем  это  (см. рис. 2.6):

          - долгота  W  восходящего  узла  -  точки  перехода ИСЗ из южного в северное полушарие,

          - угол i  наклонения  орбиты,  т. е.  угол  между плоскостью орбиты  и плоскостью  экватора;

          - аргумент (угол) перигея wмежду радиусами-векторами перигея и  восходящего узла (иногда в рассмотрение вводят вводят угол       u=w+q, который называют фазой ИСЗ или аргументом широты).

2.3.3. В разделе 2  пока  рассматривалась идеализированная модель   воздействия на ИСЗ лишь центрального поля тяготения при отсутствии возмущающих сил. Однако Земля неоднородна и не шарообразна, на ИСЗ воздействует «солнечный ветер» и т.п. Эти возмущающие факторы (хотя и на 5-6 порядков меньше, чем центральное гравитационное поле) приводят к необходимости полагать  отмеченные выше шесть параметров W(t). I(t),w(t), a(t), b(t), t_П(t) медленно меняющимися во времени. Причем вводят так называемые  оскулирующие параметры, определяемые на некоторый интервал времени в предположении отсутствия возмущений. В системе GPS изменения параметров учитываются в виде аддитивных поправок, имеющих вид линейной комбинации синуса и косинуса удвоенного (также исправленного) аргумента широты. Используемые в служебном сообщении оскулирующие параметры и  поправки приведены  в приложении.

В служебном сообщении СРНС GPS  передаваемые оскуллирующие элементыотнесены к наперед заданному  моменту времени    t_ос (опорному моменту  времени  эфемерид), являющемуся примерно серединой часового отрезка,  на котором необходимо выполнить прогноз координат и скорости  ИСЗ.  На  момент t_ос сообщается  шесть кепплеровских параметров:

1) средняя аномалия M_o,

2)   корень квадратный из большой  полуоси  эллипса Ö a,

3)  долгота восходящего узла (в Гринвичской системе координат) W₀,

4)  наклонение орбиты i_0,

5)  эксцентриситет e,

6)   аргумент перигея w.

Передаются две константы: гравитационная постоянная Земли m=3.986008.10¹⁴м³/с², угловая скорость Земли W=7.2922115147.10^-5с^-1, и значения 4-х величин:

1)  отклонение среднего движения спутника от расчетной величины Dn,

2)  скорость прецессии  восходящего узла W_a,

3)  коэффициентов формулы (1.6) для поправки шкалы времени ИСЗ,

            

21

4) интервала времени t_l-t_ос,где t_l-момент времен  последних измерений,  по которым   на Земле   вычислялись данные,   закладываемые затем в память спутника.

Эта  разность, отображающая возраст эфемерид,  передается словом  AODE     в  начале и  конце  эфемерид.   По этому  слову можно  судить о степени надежности  данных,  получаемых потребителем от спутника.

Передаются и три пары амплитуд косинусной и синусной гармоник соответственно для трех поправок:

22

1)  широты  C_uc,  C_us ,

2)  радиусу орбиты  C_rc,  C_ur,,

3)  углу наклонения  C_ic,  C_is.                                                                                                                                                                 

По принятому сообщению в АП  вычисляются:

1) большая  полуось эллипса                                                    a=(Öa)²,

  

        2) средняя угловая скорость ИСЗ                                            n_o= 2p /T =Öm/a³,

        3)  время прогноза (для k-го момента)                                     t_k=t-t_ос,

4) скорректированная средняя угловая скорость ИСЗ            n =n_o+Dn,

        5) средняя аномалия M_k=M_o+n t_k .

По  полученным и расчетным данным решается  уравнение Кеплера E_k-eSin E_k=M_k с определением эксцентрической  аномалии Е_k      и,  затем,  истиной аномалии q_k  - c использованием  выражений (2.8).

Далее  вычисляются:

-  неисправленный  аргумент широты       F_k=w_k+ q_k;

-  поправка  аргумента широты                  du_k=C_ussin2F_k+C_uccos2F_k;

-  поправка  радиуса                                    dr_k=C_rssin2F_k+C_rccos2F_k;

- поправка угла  наклонения  орбиты         di_k =C_issin2F_k+C_iccos2F_k;

-  исправленный аргумент широты              u_k=F_k+du_k;

-  исправленный  радиус                               r_k =a(1-e²) /(1-cosq_k)+ dr_k;

-  исправленный угол наклонения                i_k=i_o+di_k .

Эти данные позволяют сначала определить  координаты ИСЗ  в орбитальной плоскости: x_ko=-r_kcosu_k и y_ko=r_ksinu_k.

Затем вычисляют  долготу  восходящего узла в гринвичской системе

W_k=W₀+(W_а-W)t_k-Wt_oc,   после чего вычисляют гринвичские координаты

x_k=x_kocosi_kcosW_k-y_ksinW_k,             y_k=x_kocosi_ksinW_k+y_kcosW_k,                     z_k=x_kosini_k

 

с погрешностью  единиц метров при ½t_k- t_ос½£ 0.5 часа.

Производные координат ИСЗ , т.е. проекции v_xk, v_yk v_zk  вектора  линейной скорости находятся /6/ с использованием формул (2.9) для радиальной v_rk=dr_k/dt=(ma/b²)^0/5esinq_k и тангенциальной v_tk=r_kdq_k/dt =(ma/b²)^0/5(1+ecosq_k)  составляющих этого вектора:

v_xk=v_rkx_k/r_k - v_tk(sinu_kcosW_k + cosu_kcosi_ksinW_k)

v_yk=v_rky_k/r_k  - v_tk(sinu_ksinW_k + cosu_kcosi_kcosW_k)

v_zk=v_rkz_k/r_k + v_tkcosu_ksin i_k.