Автоматизация определения места судна по параметрам радионавигационной системы

                                                            Кафедра ТСС

Лабораторная работа по курсу

«Автоматизация судовождения»

АВТОМАТИЗАЦИЯ ОПРЕДЕЛЕНИЯ МЕСТА СУДНА ПО РНС

Цель работы: лабораторная работа имеет целью изучение принципов определения места судна по нескольким навигационным параметрам РНС с использованием обобщенного метода линий положения, метода наименьших квадратов (часть 1) и метода последовательных итераций (часть 2).

Краткие теоретические сведения.

В общем виде, задача определения места судна в навигационных комплексах сводится к решению систему уравнений навигационных изолиний:

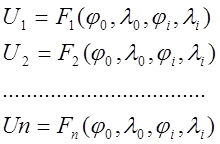                                                                                                  (1)

Где   – измеренные навигационные параметры;

 - обсервованные координаты судна;

 - координаты навигационных ориентиров (станций наземных РНС и т.д.)

Методы решения системы уравнений (1) относительно неизвестных, подразделяются на прямые и косвенные. Прямые методы предполагают непосредственное решение системы уравнений (1), что практически возможно только для несложных линейных функций  и числе уравнений не более двух. При трех и более измеренных параметрах применение прямых методов становится нецелесообразным, так как требует попарного решения уравнений системы и последующего уравнивания полученных значений.

В автоматизации судовождения находит широкое применение один из косвенных методов определения места судна - метод линий положения (ЛП) с использованием метода наименьших квадратов (МНК) и итерационной обработкой. Геометрическая сущность метода ЛП и замена криволинейных изолиний прямыми ЛП, касательными к изолиниям в точках, ближайших к счислимому месту.

Точку пересечения ЛП принимают за координаты судна в первом приближении. При числе линий положения более двух для нахождения вероятного места судна внутри фигуры погрешностей применяют МНК). Затем организуется итерационная обработка, при которой за счислимые координаты принимают координаты первого приближения, и определяются новые ЛП, которые дают точку второго приближения. Затем за счислимые координаты принимают координаты второго приближения, и так далее до тех пор, пока в результате очередной итерации (приближения) уточнение координат не станет меньше заданной погрешности расчетов.

            Алгебраически, метод ЛП сводится к линеаризации уравнений системы (1), что позволяет решать систему известными методами (методом подстановки или методом определителей), таким образом, система уравнений навигационных изолиний (1) заменяется системой линий положения:

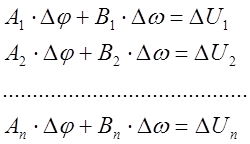                                                                                                  (2)

где        – разность обсервованных и счислимых навигационных параметров;

       –проекция градиентов изолиний на меридиан и параллель;

 – модуль градиента;

 – направление градиента.

            Но, так как каждое измерение навигационного параметра содержит погрешности, система уравнений (2) получается несовместной, т.е. не имеет единственного решения. (ЛП не пересекаются в одной точке). Разрешить это противоречие помогает МНК, позволяющий найти вероятное место судна при условии, что сумма квадратов погрешностей минимальна.

            Чтобы система уравнений (2) стала совместной, вместо  подставим , где   – неизвестная поправка измерения, и преобразуем систему уравнений ЛП (2) в систему уравнений поправок:

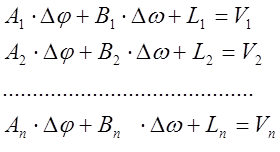                                                                                            (3)

uде  –свободный член уравнения поправок.

Далее, возводим в квадрат и суммируем левые и правые части уравнений системы (3):

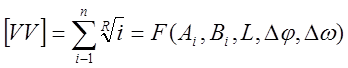                                                                               (4)

Для нахождения ,   при которых ,  найдем частные производные функции  по переменным  Δj,  Δw   и приравняем их к нулю. Выполнив при этом несложные алгебраические преобразования, получим систему двух нормальных уравнений Гаусса:

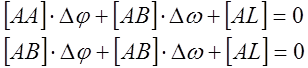                                                                                   (5)

                                       где  

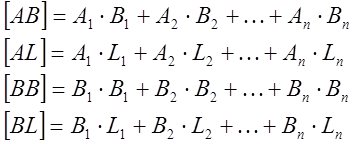
Таким образом, система двух нормальных уравнений (5) содержит два неизвестных   и может быть решена методом определителей:

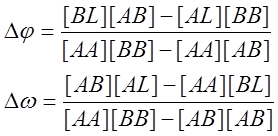                                             (6)

Вероятное место судна рассчитывается по формулам:

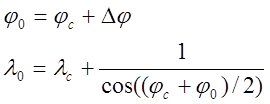                                           (7)

Коэффициенты  систем уравнений (2) или (3), рассчитывают через модуль  и направление  градиента навигационного параметра для разностно-дальномерных РНС.

В окончательном виде:

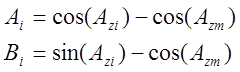
                                            (8)

где   - счислимый азимут ведомой станции;

 – счислимый азимут ведущей станции.

Свободные члены  уравнений поправок рассчитываются по формулам:

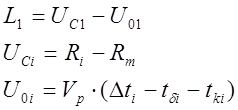                                          (9)

где  – счислимое расстояние до ведомой станции, мили;

 – счислимое расстояние до ведущей станции, мили;

  – измеренный радионавигационный параметр, мкс;

  - базовая задержка, мкс;

 - кодовая задержка, мкс;

 мили/ мкс – скорость распространения радиоволн.

Счислимые азимуты и расстояния могут быть рассчитаны по формулам сферической тригонометрии через счислимые координаты, и координаты станций  :

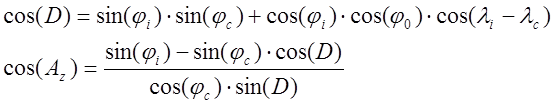                            (11)

Но, для обеспечения точности расчетов, счислимые расстояния необходимо затем уточнить для выбранной модели эллипсоида:

..  (12)

Порядок выполнения работы:

В порядке предварительной подготовки необходимо ознакомиться с теоретическими основами определения места судна с использованием МНК, и методом итераций.

Часть 1.

В первой части работы исследуются особенности МНК при определении места судна по трем ЛП. Каждая ЛП задается азимутом переноса , величиной переноса (n) и градиентом () в соответствии с уравнением:

,

где ,     

,

.

Необходимо проанализировать изменение вероятного места судна в треугольнике погрешностей в следующих случаях:

1.  При изменении азимутов и неизменных переносах (1, 1, 1) и градиентах (1, 1, 1);

2. При  изменении переносов и неизменных азимутах (0, 45, 90) и градиентах (1, 1, 1).

3.  При изменении градиентов и неизменных азимутах (0, 45, 90) и переносах

(1, 1, 1).

Для каждого случая зарисовать с экрана несколько характерных ситуаций, сделать соответствующие выводы (как изменяется форма треугольника погрешностей, и как меняется обсервованное место судна).

Часть 2.

Во второй части работы исследуется определение места судна по цепи 9970 РНС «Лоран-С». При исследовании с радионавигационной карты снимаются отсчеты навигационного параметра для станций W, X, Y, Z дающие треугольник погрешностей со сторонами в несколько миль, и счислимые координаты, выбранные в 30 – 60 милях от обсервованного места.

      1. Ввести данные, соответствующие базовой линии станции X и начальные данные, в соответствие с диалогом на экране компьютера.

2. Описать итерационный процесс расчета обсервованных координат. Зарисовать с экрана графические построения для всех итераций.

      3. Провести три серии опытов с разными начальными данными, исследуя влияние следующих факторов:

- перемещение вдоль базовой линии станции X;

-  удаление от базовой линии станции X;

-  погрешности измерения навигационного параметра станции W, кратной 10 мкс, на погрешность определений места судна в Японском море.

Для каждой серии опытов зафиксировать результаты в цифровом виде (для последней итерации), сделать соответствующие выводы.