Программирование на языке «Ядро»: Руководство пользователя, страница 10

Основное назначение языка «Ядро», для которого он был разработан, заключается в задании данных о конечно-элементных моделях. Интерпретатор «Ядро» входит в состав пакета программ «Композит 2005» и разрабатываемых последующих версий этой серии программных продуктов. Поэтому в настоящем разделе описывается применение языка «Ядро» для задания данных в формате пакета «Композит 2005».

Данные о конечно-элементных моделях конструкций включают ряд таблиц, с помощью которых задается положение узлов расчетной конечно-элементной сетки, внутренняя и внешняя геометрия, топология сетки, жесткостные свойства, материалы, воздействия и кинематические условия закрепления. Такая структура данных является достаточно традиционной при расчетах конструкций методом конечных элементов. Программа на языке «Ядро» является исходным кодом, в результате интерпретации которого генерируются таблицы данных для МКЭ-процессора. Формат входных таблиц МКЭ-процессора описывается по мере рассмотрения различных аспектов строения конечно-элементных моделей.

2.1. Задание координат узлов

Пространственная сетка состоит из узлов, положение которых задается координатами в общей системе координат. Координаты всех узлов, в порядке их нумерации, должны быть занесены в таблицу, каждая строка которой содержит три вещественных числа – абсциссу, ординату и аппликату узла.

На языке «Ядро» удобно формировать эту таблицу в виде массива вещественных чисел, который везде в дальнейшем будет именоваться XYZ:

real XYZ[NXYZ,3];

целая переменная NXYZ содержит число узлов сетки.

2.1.1. Равномерные сетки в пространстве и на плоскости

Выше уже приводились примеры задания координат узлов равномерных сеток на плоскости. Для полноты картины рассмотрим также равномерные сетки в пространстве. Пусть, например, прямоугольный параллелепипед размерами  вдоль осей X, Y, Z вдоль каждой из сторон делится на равные отрезки числом m, n и p соответственно. Все необходимые параметры считаем описанными и заданными в охватывающем блоке.

Заполним вначале вспомогательные массивы абсцисс, ординат и аппликат:

real  (X[m+1], Y[n+1], Z[p+1]); {число узлов по оси на 1 больше числа отрезков}

X:=0 to a numb m+1; Y:=0 to b numb n+1; Z:=0 to c numb p+1;

Далее эти значения надо поместить в таблицу в нужном порядке. Размер таблицы координат переопределим по числу узлов:

XYZ realloc (p+1, n+1, m+1, 3);

{узлы нумеруются вначале вдоль оси X, затем Y, в последнюю очередь – вдоль оси Z}

NXYZ:=(p+1)*(n+1)*(m+1); {общее число узлов}

Вдоль каждой линии сетки, параллельной оси X, необходимо задать значения абсцисс из массива X.

XYZ[,1]:=X repeat;

Значения ординат будут постоянными на каждой такой линии. При этом в каждом сечении, перпендикулярном оси Z, число линий сетки равно длине массива Y, и каждое значение ординаты должно повторяться по числу узлов в линии, равному m+1. Ординаты в каждом следующем сечении повторяются.

XYZ[,2]:=(Y repscal (m+1)) repeat;

Наконец, аппликаты постоянны в каждом сечении, перпендикулярном Z, и поэтому каждое значение из массива Z необходимо повторить столько раз, сколько узлов содержится в сечении.

XYZ[,3]:=Z repscal;

В результате интерпретации в текстовый файл выгружается таблица координат равномерной сетки:

integer i;

XYZ[i,] dsply ‘coord.txt’ on i from 1:NXYZ;

Таким образом, для задания координат равномерной сетки достаточно таких средств языка «Ядро», как прогрессии и повторители.

Несколько сложнее генерация координат узлов равномерной сетки, состоящей из равносторонних треугольников. Расчетная область должна допускать разбивку на треугольники; возьмём в качестве примера треугольную область, основание которой находится на оси X, а ось Y проходит через узел на основании (рисунок 9). Число отрезков сетки на каждой из сторон треугольника равно n, длина стороны a. Нумеровать узлы будем вначале вдоль основания в сторону возрастания абсциссы, затем – по горизонтальным рядам слева направо и снизу вверх.

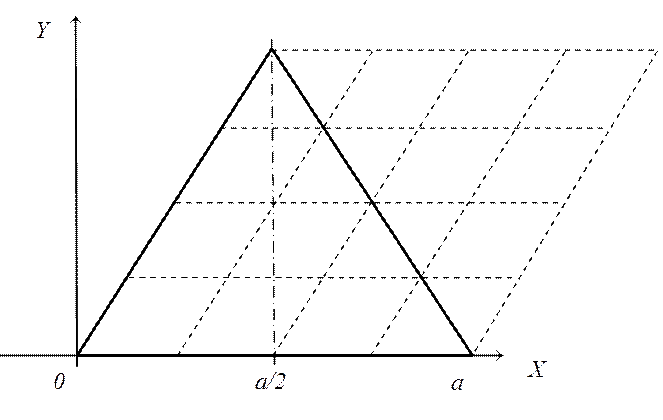
Рисунок 9. Равномерная сетка на треугольнике и охватывающий параллелограмм

Как видно из рисунка, каждый горизонтальный ряд содержит на один узел меньше, чем соседний ряд снизу, поэтому неудобно формировать координаты в прямоугольной таблице, как это было сделано выше.

Дополним треугольную область до параллелограмма, как показано на рисунке 9. Координаты вспомогательной сетки на параллелограмме поместим во временные массивы X и Y:

real (X,Y)[n+1,n+1];

X:=(0 to a numb n+1) repeat; X:+ (0 to a/2 numb n+1) repscal;

Y:=(0 to a*sin1 60 numb n+1) repscal;

При формировании массива Х вначале, как в предыдущем примере, он заполняется повторяющейся последовательностью абсцисс узлов первого горизонтального ряда, а затем к абсциссам узлов каждого ряда добавляются, повторяясь нужное число раз, элементы прогрессии, равные абсциссам первого узла каждого ряда.

Теперь остается выбрать из вспомогательных массивов координаты только тех узлов, которые попадают в треугольную область. Число таких узлов равно (n+1)(n+2)/2. Перераспределим память массива XYZ в соответствии с этим размером и используем циклическое выражение для выборки значений из строки вспомогательного массива, ограничив число выбираемых элементов строки: из первой строки будет выбрано n+1 значение, из второй – на одно меньше и т.д.:

NXYZ:=(n+1)*(n+2)/2;

XYZ realloc (NXYZ, 3);

integer I;

XYZ[,1]:=X[I,:n+2-I] on I from 1:n+1;

XYZ[,2]:=Y[I,:n+2-I] on I from 1:n+1;

Осталось задать третью координату равной нулю и выгрузить массив в текстовый файл:

XYZ[,3]:=0;

XYZ[I,] dsply ‘coord.txt’ on I from 1:NXYZ;

При большом числе узлов сетки использование вспомогательных массивов может привести к излишним затратам времени вычислений и памяти компьютера. Поэтому рассмотрим ещё один способ задания координат с помощью циклов. Заметим, что используемые компоненты вспомогательных массивов находятся в треугольнике, в котором сумма двух индексов не превышает n+1, и выразим координаты узлов через два параметра – индекс по горизонтали и индекс по вертикали:

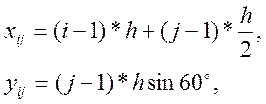
где h – шаг сетки по горизонтали,

индекс j пробегает значения от 1 до n+1, индекс i – от 1 до n+2-j. Тогда массив XYZ может быть заполнен следующим образом:

real h; h:=a/n;

XYZ[,1]:=(((i-1)*h+(j-1)*h/2) on i from 1:n+2-j) on j from 1:n+1;

XYZ[,2]:=(( (j-1)*h*sin1 60) on i from 1:n+2-j) on j from 1:n+1;

XYZ[,3]:=0;

На рисунке 10 приведен текст на языке «Ядро» и полученные данные.

  

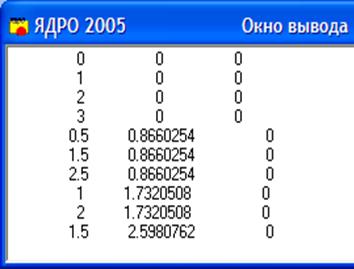
Рисунок 10. Пример вычисления координат на треугольнике