Вывод: дисперсии по переменной «Рост» у студентов 1-2 и 3-4 курсов равны,
средний рост студентов 1-2 и 3-4 (171.04 см. и 170.75 см.) курсов значимо равны.
Переменная: жизненная ёмкость легких
Гипотезы.
Н0: средняя ёмкость легких студентов 1-2 курсов не отличается от средней ёмкость легких студентов 3-4 курсов;
Н1: средняя ёмкость легких студентов 1-2 курсов отличается от средней ёмкость легких студентов 3-4 курсов.
Group Statistics
|
Пол |
N |
Mean (среднее) |
Std. Deviation (СКО) |
Std. Error Mean (Стандартная ошибка среднего) |
|||
|
Ёмкость легких. |
1-2 2005-2006 |
759 |
2.547 |
.6446 |
.0234 |
||
|
3-4 2008-2009 |
593 |
2.333 |
.5697 |
.0234 |
|||
Independent Samples Test
|
Ёмкость легких. |
Levene's Test for Equality of Variances (Тест Левина на равенство дисперсий) |
t-test for Equality of Means (Тест Стьюдента на равенство средних) |
||||||||
|
F |
Sig. (Значимость) |
t |
df (число степеней свободы) |
Sig. (2-tailed) (Значимость) |
Mean Difference (Разность средних) |
Std. Error Difference (Стандартная ошибка разницы) |
95% Confidence Interval of the Difference (Довер.интерразницы) |
|||
|
Lower (Нижняя граница) |
Upper (Верхняя граница) |
|||||||||
|
Equal variances assumed (Дисперсииравны) |
22.255 |
.000 |
6.349 |
1350 |
.000 |
0.2133 |
0.0336 |
0.1474 |
0.2791 |
|
|
Equal variances not assumed (Дисперсиинеравны) |
6.446 |
1329.6 |
.000 |
0.2133 |
0.0331 |
0.1483 |
0.2782 |
|||
Вывод: дисперсии по переменной «Жизненная ёмкость легких» у студентов 1-2 и 3-4 курсов не равны,
средняя ёмкость легких студентов 1-2 и 3-4 (2.547 и 2.333) курсов значимо не отличаются.
Переменная: пульс
Гипотезы.
Н0: средний пульс студентов 1-2 курсов не отличается от среднего пульса студентов 3-4 курсов;
Н1: средний пульс студентов 1-2 курсов отличается от среднего пульса студентов 3-4 курсов.
Group Statistics
|
Пол |
N |
Mean (среднее) |
Std. Deviation (СКО) |
Std. Error Mean (Стандартная ошибка среднего) |
|||
|
Пульс |
1-2 2005-2006 |
759 |
88.0 |
15.81334 |
.57399 |
||
|
3-4 2008-2009 |
593 |
92.9 |
15.18394 |
.62353 |
|||
Independent Samples Test
|
Пульс |
Levene's Test for Equality of Variances (Тест Левина на равенство дисперсий) |
t-test for Equality of Means (Тест Стьюдента на равенство средних) |
||||||||
|
F |
Sig. (Значимость) |
t |
df (число степеней свободы) |
Sig. (2-tailed) (Значимость) |
Mean Difference (Разность средних) |
Std. Error Difference (Стандартная ошибка разницы) |
95% Confidence Interval of the Difference (Довер.интерразницы) |
|||
|
Lower (Нижняя граница) |
Upper (Верхняя граница) |
|||||||||
|
Equal variances assumed (Дисперсииравны) |
5.185 |
.023 |
-5.806 |
1350 |
.000 |
-4.94530 |
.85173 |
-6.61617 |
-3.27443 |
|
|
Equal variances not assumed (Дисперсиинеравны) |
-5.835 |
1294.4 |
.000 |
-4.94530 |
.84750 |
-6.60792 |
-3.28268 |
|||
Вывод: дисперсии по переменной «Пульс» у студентов 1-2 и 3-4 курсов не равны,
Средний пульс студентов 1-2 и 3-4 (88 и 92.9) курсов значимо не отличаются.
Лариса Ал-на, не знаю, как обрабатывать Пробы. Можно ли по ним считать среднее значение ?
Частотное распределение по курсам
|
Курс |
Частота |
|
1-2 2005-2006 г |
759 |
|
3-4 2008-2009 |
593 |
Задание 1. Построить ряды распределения студентов по курсам по уровням физических показателей, сделать вывод.
1) Индекс массы тела.
Уровни:
дистр. – дистрофия;
норма – норма;
ожир. – ожирение.
|
Курс |
дистр. |
норма |
ожир. |
Сумма |
|
|
К |
с1-2 курс 2005-2006 г |
41,1% |
54,2% |
4,7% |
100,0% |
|
3-4 курс 2008-2009 |
30,0% |
55,3% |
14,7% |
100,0% |
|
Проверим разницу в уровнях индекса массы тела по курсам на значимость различий используя угловое преобразование Фишера.
Уровень внимания = «дистрофия»
Сравним разницу между 1-2 курсом (41.1%) и 3-4 курсом (30,0%)
H0: Доля лиц, с дистрофией, на 3-4 курсе не больше, чем на 1-2 курсе.
H1: Доля лиц, с дистрофией, на 3-4 курсе больше, чем на 1-2 курсе.
Определяем величины j, соответствующие процентным долям в каждой выборке j1(41,1)=1,392 j2(30,0)=1,159.
Теперь подсчитаем эмпирическое значение j*:
j*эмп=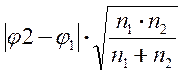
=
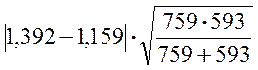=4,25.
При уровне значимости 5% j*кр=1,64.
j*эмп>j*кр значит Н0 отвергается.
Таким образом, на уровне значимости 5% доля лиц, с дистрофией, на 3-4 курсе больше, чем на 1-2 курсе.
Уровень внимания = «норма»
Сравним разницу между 1-2 курсом (54,2%) и 3-4 курсом (55,3%)
H0: Доля лиц, с нормой, на 3-4 курсе не больше, чем на 1-2 курсе.
H1: Доля лиц, с нормой, на 3-4 курсе больше, чем на 1-2 курсе.
Определяем величины j, соответствующие процентным долям в каждой выборке j1(54,2)=1,655 j2(55,3)=1,677.
Теперь подсчитаем эмпирическое значение j*:
j*эмп==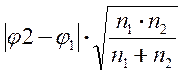
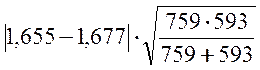=0,40.
При уровне значимости 5% j*кр=1,64.
j*эмп<j*кр значит Н0 принимается.
Таким образом, на уровне значимости 5% доля лиц, с нормой, на 3-4 курсе не больше, чем на 1-2 курсе.
Уровень внимания = «ожирение»
Сравним разницу между 1-2 курсом (4,7%) и 3-4 курсом (14,7%)
H0: Доля лиц, с нормой, на 3-4 курсе не больше, чем на 1-2 курсе.
H1: Доля лиц, с нормой, на 3-4 курсе больше, чем на 1-2 курсе.
Определяем величины j, соответствующие процентным долям в каждой выборке j1(4,7)=0,437 j2(14,7)=0,787.
Теперь подсчитаем эмпирическое значение j*:
j*эмп==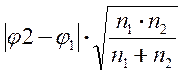
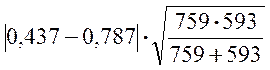=6,39.
При уровне значимости 5% j*кр=1,64. j*эмп>j*кр значит Н0 отвергается.
Таким образом, на уровне значимости 5% доля лиц, с ожирением, на 3-4 курсе больше, чем на 1-2 курсе.
2) Весо-ростовой показатель.
Уровни:
дисгармон. – дисгармония;
норма – норма;
|
Курс |
дисгармон. |
норма |
Сумма |
|
|
К |
с1-2 курс 2005-2006 г |
11,7% |
88,3% |
100,0% |
|
3-4 курс 2008-2009 |
13,5% |
86,5% |
100,0% |
|
Проверим разницу в уровнях индекса массы тела по курсам на значимость различий используя угловое преобразование Фишера.
Уровень внимания = «дисгармония»
Сравним разницу между 1-2 курсом (11.7%) и 3-4 курсом (13,5%)
H0: Доля лиц, с дисгармонией, на 3-4 курсе не больше, чем на 1-2 курсе.
H1: Доля лиц, с дисгармонией, на 3-4 курсе больше, чем на 1-2 курсе.
Определяем величины j, соответствующие процентным долям в каждой выборке j1(11,7)=0,698 j2(13,5)=0,752.
Теперь подсчитаем эмпирическое значение j*:
j*эмп==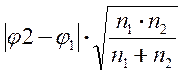
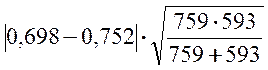=0,99.
При уровне значимости 5% j*кр=1,64.
j*эмп<j*кр значит Н0 принимается.
Таким образом, на уровне значимости 5% доля лиц, с дисгармонией, на 3-4 курсе не больше, чем на 1-2 курсе.
Уровень внимания = «норма»
Сравним разницу между 1-2 курсом (88,3%) и 3-4 курсом (86,5%)
H0: Доля лиц, с нормой, на 3-4 курсе не больше, чем на 1-2 курсе.
H1: Доля лиц, с нормой, на 3-4 курсе больше, чем на 1-2 курсе.
Определяем величины j, соответствующие процентным долям в каждой выборке j1(88,3)=2,443 j2(86,5)=2,389.
Теперь подсчитаем эмпирическое значение j*:
j*эмп==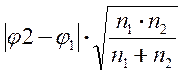
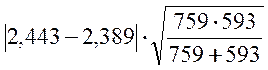=0,99.
При уровне значимости 5% j*кр=1,64.
j*эмп<j*кр значит Н0 принимается.
Таким образом, на уровне значимости 5% доля лиц, с нормой, на 3-4 курсе не больше, чем на 1-2 курсе.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.