Цифровое моделирование непрерывных систем, страница 2

1.3. Задать шаг моделирования 0.01 с. Замерить значения процесса для  t, равного 1с и 2 с для четырех методов численного интегрирования: Эйлера, Рунге-Кутта 2-го порядка, Рунге-Кутта 4-го порядка и обратного метода Эйлера. Уменьшить шаг моделирования до 0.1 с и проделать те же измерения. Результаты измерений свести в таблицу, объяснить их.

2. Исследование влияния шага модельного времени на форму переходной характеристики интегрирующей цепи.

1 1 + рТ

2.1 Записать дифференциальное уравнение для интегрирующей цепи, описываемой передаточной функцией К(р) =            .. Составить графическую модель устройства.

2.1. Собрать на рабочем столе составленную модель, взяв значение постоянной времени Т из таблицы:

Вариант	1	2	3	4	5	6	7	8	9	10
Т, с	0.1	0.4	0.8	0,2	0,5	0,9	0,3	0,6	1,0	0,7

Сумматор можно перевести в вычитающее устройство, подведя указатель мыши к нужному входу и, когда он превратится в вертикальную стрелку, щелкнуть правой кнопкой мыши.

2.2. Установить шаг моделирования 0,1Т , время моделирования 10Т и алгоритм интегрирования – Эйлер. Для удобства сравнения процессов при различных условиях моделирования перевести осциллограф (Plot) в режим сохранения следов. Для этого щелкнуть правой кнопкой мыши на осциллографе. В раскрывшемся окне активировать опцию Over plot и установить Plot points равным 4, что будет соответствовать сохранению четырех следов. Желательно, чтобы следы имели разные цвета, поэтому при изменении условий моделирования выход модели подсоединяйте к другому входу. Запустить моделирование. Изменить алгоритм интегрирования на Рунге-Кутта 4-го порядка, зафиксировать переходную характеристику. Проделать это же для обратного метода Эйлера. Полученные переходные характеристики нужно сравнить с точной. Переходная характеристика будет близка к точной, если интегрирование провести методом Рунге-Кутта 4-го порядка при шаге равном 0.001Т. Сравните переходные характеристики (одним – двумя предложениями), при необходимости зарисуйте их. Очистить экран осциллографа, для чего щелкнуть на нем правой кнопкой мыши и в раскрывшемся окне нажать на кнопку Clear Display.

2.3. Повторить измерения, проделанные в п. 2.2. для других значений шага моделирования: 0.5Т, Т, 2Т и 3Т. Отметить, при каком шаге моделирования для каждого метода полученная переходная характеристика значительно отличается от точной и когда процесс становится неустойчивым. Объяснить неустойчивость решения по методу Эйлера.

2.4. Смоделировать интегрирующую цепь как линейное звено (Blocks ® Linear System ® transferFunction). Параметры блока: Gain – 1, Numerator – 1, Denjminator – T_1. Просмотреть переходные характеристики для различных значений шага моделирования (0,1Т, 0,5Т, Т, 2Т и 3Т).Сделать выводы о влиянии шага моделирования на рассчитанное значение переходной характеристики.

3. Исследование влияния шага модельного времени на ошибки моделирования замкнутых систем.

3.1. Смоделировать замкнутую систему, заданную следующей схемой:

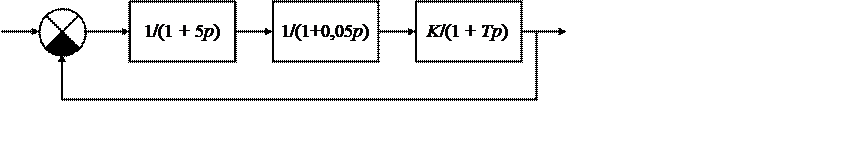Значения К и Т взять из таблицы:

Вариант	1	2	3	4	5	6	7	8	9	10
К	40	50	65	80	100	40	50	65	80	100
Т, с	0,05	0,033	0,02	0,012	0,008	0,04	0,025	0,017	0,01	0,007

3.2. Замерить частоту среза w_ср, то есть частоту, на которой ЛАХ разомкнутой  системы  пересекает  ось  частот  (АЧХ  разомкнутой  системы К_р(w_ср) = 1). Для чего выделить разомкнутую систему. Щелкнуть на Analyze ® Frequency Response. Для измерения использовать перекрестие.

3.3. Замерить граничную частоту, за которую примем частоту, на которой АЧХ замкнутой системы К_з(w_гр) = 0,1. Выделить замкнутую систему. Щелкнуть на Analyze ® Frequency Response. По вертикальной оси установить равномерную шкалу. Сравнить граничную частоту и частоту среза. Перейти от круговой частоты к обычной f_гр = w_гр/2p.

3.4. Просмотреть и провести качественное сравнение переходных характеристик замкнутой системы при различных значениях шага модельного времени Step Size. Для удобства сравнения использовать Plot в режиме сохранения следов (активизировать Over Plot). Установить начальное значение Step Size 0,0001c. Полученную переходную характеристику можно считать точной. Далее использовать следующий ряд значений Step Size: 0,001; 0,01; 0,02; 0,04; 0,08. Зарисовать эти переходные характеристики. Сравнить их.

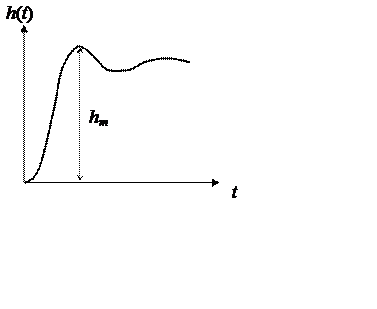3.5. Провести количественную оценку влияния шага модельного времени на точность моделирования. За показатель точности примем величину первого выброса в переходной характеристике h_m, а отношение Dh_m/h_m – за относительную ошибку моделирования. Здесь Dh_m – разность между h_m при выбранном шаге моделирования и точном значении h_m, полученном при очень малом шаге.

Результаты измерений свести в таблицу:

Шаг моделирования Dt	0,0001	0,001	0,01	0,02	0,04	0,08
hm
Dhm/hm точн
fгрDt
1/fгрDt = fдискр/fгр

Построить зависимость относительной ошибки моделирования от отношения частоты дискретизации к граничной частоте. Сделать вывод о требуемом значении этого отношения, чтобы ошибка моделирования не превышала нескольких процентов.

Контрольные вопросы

1 Какие ошибки возникают при замене непрерывной системы цифровой моделью? Как уменьшить эти ошибки?

2. Как производится численное решение дифференциального уравнения явным методом Эйлера? Почему решение, полученное этим методом в пп. 1.2 и 1.3, ниже точного решения, а полученное в пп. 2.2 и 2.3 выше точного?

3. В чем отличие неявного (обратного) метода Эйлера от явного метода Эйлера? Как объяснить, что решения, полученные этими методами, располагаются по разные стороны от точного?

4. Почему при большом шаге Δt решение может стать неустойчивым? Объяснить периодичность решения, полученного в п. 2.3 при Δt = 2Т.

5. Как по дифференциальному уравнению составляется модель для работы в VisSim? Составить модель для уравнения, заданного преподавателем.

6. Как записывается дифференциальное уравнение по передаточной функции? Записать уравнение по заданной преподавателем передаточной функции.

7. Как рассчитывается выходной процесс для линейных звеньев, заданных передаточными функциями? Объяснить результаты моделирования по п. 2.4. Как влияет величина шага Δt на ошибку моделирования?

8. Как влияет величина шага моделирования Δtна результаты моделирования замкнутых систем? При каком значении Δtf_гр, судя по результатам моделирования, ошибка моделирования менее 10 %?

9. Как записывается передаточная функция линейного звена, заданного transferFunction с параметрами: Gain – 1, Numenator – 1, Denominator – 1_0? Какие методы численного решения используются при задании интегратора как блока integrator и как блока transferFunction?