Построение алгоритма метода оптимизации. Реализация алгоритма с помощью набора “стандартных” средств программы Excel предполагает построение структуры логической схемы, приводящей к конечному оптимальному решению. Алгоритмы методов оптимизации, которые в соответствии с заданиями данных методических рекомендаций необходимо будет реализовывать, можно найти в литературе [3, 4]. Здесь мы приводим общую структуру, которая характерна для алгоритмов методов оптимизации. Эту структуру следует использовать при реализации конкретных алгоритмов.
Структура алгоритма должна включать следующие этапы.
1. Начальный этап.
Задание начального приближения X(0), исходных параметров алгоритма a(0), требуемой точности e; начальных значений счетчика количества итераций k = 0 и количества расчетов целевой функции N = 0; значение параметра верхней границы Nmax, при достижении которой в случае “зацикливания” программа должна завершить свою работу.
2. Основной этап.
2.1. Расчет новой координаты в соответствии с математической сущностью метода
X(k+1) = X(k) + j[X(k), f(X(k)), P(f(X(k)))],
где j, P - операторы метода оптимизации.
2.2. Проверка условия нахождения оптимума и достижения верхних границ параметра N.
Если D £ e, то перейти к этапу 3.
Если N ³ Nmax, то перейти к этапу 3.
D – оценка текущей точности.
2.3. Выдача полученных значений переменных и параметров k, X(k), f(X(k)), D.
2.4. Адаптация параметров алгоритма a(k).
2.5. Наращивание номера итерации k = k + 1 и переход к этапу 2.
3. Завершение процесса нахождения оптимума. Выдача полученных результатов.
Реализация алгоритма метода заключается в построении табличного варианта, в котором столбцы описывают переменные и параметры метода, а строки – итерации, и предусматривает введение в ячейки рабочего листа исходных данных, расчетных операций и установление логических связей между ячейками. Все ячейки при реализации можно разбить на три группы:
- группа ячеек с исходными данными, не изменяемыми в ходе работы метода (например, точность);
- строка, содержащая данные по “нулевой итерации”, т.е. исходные значения параметров, изменяемых в ходе процесса оптимизации (например, начальные границы интервала, начальный шаг и т.д.);
- строки, содержащие изменение параметров, указанных в строке “нулевой итерации” строки.
Как правило, при правильной записи процедуры изменения параметров, в третьей группе ячеек достаточно описать только строку для первой итерации. Строки для последующих итераций получаются путем копирования. Последней строкой будет считаться та, в которой будет достигнуто значения критерия оптимизации.
Задача 1.
Постановка задачи. Cоставить алгоритм нахождения в заданном интервале [a, b] с требуемой точностью e экстремума функции f(x) одной переменной методом половинного деления.
Алгоритм метода.
Начальный этап. Выбрать константу e > 0, допустимую конечную длину интервала l > 0, начальный интервал [a0, b0]. Задать k = 0 и перейти к основному этапу.
Основной этап. Шаг 1. Если bk - ak < l то остановиться. Точка минимума принадлежит интервалу [ak, bk]. Иначе вычислить
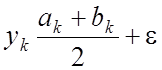
и перейти к шагу 2.
Шаг 2. Если f(xk) < f(yk), то ak+1 = ak и bk+1 = yk. В противном случае положить ak+1 = yk и b k+1= bk. Заменить k = k + 1 и перейти к шагу 1.
Реализация метода. На рис. 2.1 приведено
содержание ячеек рабочего листа, используемых для осуществления первых двух
итераций при нахождении данным методом минимума функции
f(x) = (x - 2)2 + 7
при начальном интервале [‑20, 20], конечной длине интервала 0,005 и константе различимости
0,001.
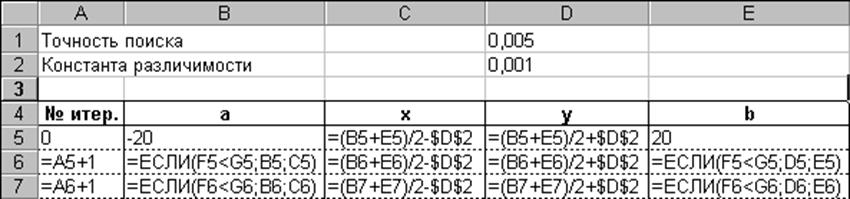
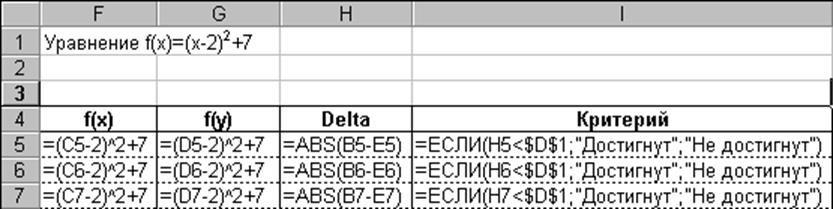
Рис. 2.1. Содержание ячеек при реализация
метода
половинного деления
Результаты решения задачи для условий, описанных выше, приведены на рис. 2.2.
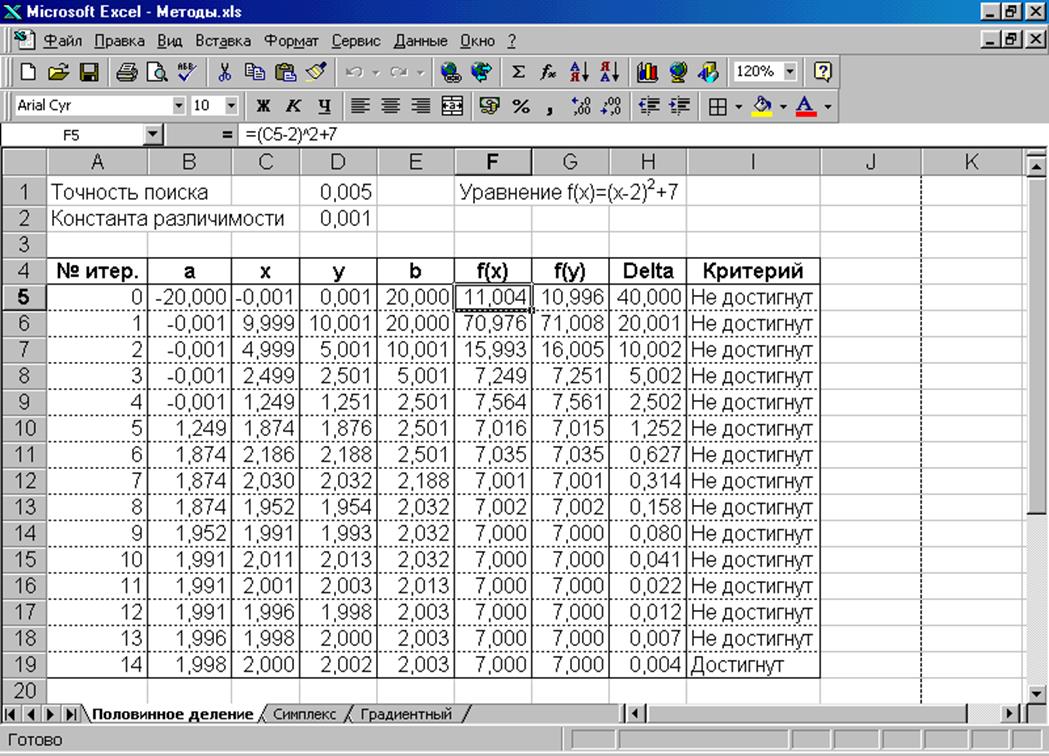
Рис. 2.2. Результаты поиска минимума функции методом половинного деления
Задача 2.
Постановка задачи. Cоставить алгоритм нахождения с требуемой точностью e экстремума функции f(X) двух переменной симплекс-методом с изменяемой длиной ребра. Начальное расположение симплекса – одна из вершин в начале координат.
Алгоритм метода.
1. Начальный этап. Расчет координат симплекса в соответствии с таблицей
|
№ |
x1 |
x2 |
|
1 |
0 |
0 |
|
2 |
P |
Q |
|
3 |
Q |
P |
где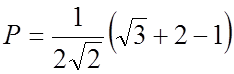 
,
.
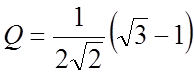Задать k = 0.
2. Определение вершин с максимальным и минимальным значением функции. Определяют те вектора X многогранника, которые дают максимальное и минимальное значение f(X), а именно
f(Xh(k)) = max{f(X1(k)), ..., f(Xn+1(k))};
f(Xl(k)) = min{f(X1(k)), ..., f(Xn+1(k))}.
3. Расчет координат центра тяжести. Координаты центра тяжести рассчитываются по формуле
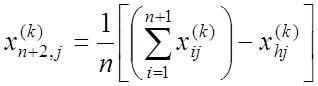, j =1, …, n,
где индекс j обозначает координатное направление.
Если на k-1 этапе произошла редукция, то перейти к шагу 5, иначе к шагу 4.
4. Определение зацикливания. Зацикливание происходит в случае, если номера вершин с максимальным значением f(X) совпадают на k-ом и (k-1)-ом шагах, т.е.
h(k) = h(k-1).
Если зацикливание не обнаружено, то переход к этапу 5, в противном случае происходит проверка условия окончания поиска
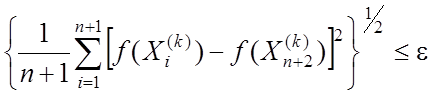
В случае выполнения условия переход к этапу 7, иначе к этапу 6.
5. Отражение. Представляет проектирование Xh(k) через центр тяжести в соответствии с соотношением
.
Установить k = k + 1 и перейти к этапу 2.
6. Редукция. Расчет координат вершин симплекса осуществляется в соответствии с формулой
Xi(k+1) = Xl(k) + 0,5(Xi(k) - Xl(k)), i = 1, …, n + 1.
Установить k = k + 1 и перейти к шагу 2.
7. Выдача полученных результатов. В качестве решения задачи взять вершину с минимальным значением f(X).
Реализация метода. На рис. 2.3 приведено
содержание ячеек рабочего листа, используемых для осуществления первых двух
итераций при нахождении данным методом минимума функции
f(X) = (x1 - 2)2 + (x2 - 3)2
при начальной длине ребра, равной 1, и точности
поиска 0,01
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.