Происхождение и смысл понятия «Синергетика». Отличие подходов в кибернетике и синергетике. Принцип порядка Больцмана. Два принципа асимметрии природы на примерах преобразования энергии. Вывод уравнения Ланжевена

1) Происхождение и смысл понятия «Синергетика».

Термин синергетика предложил ввести Г. Хакен. Это название происходит от греческого synergeia, что означает совместное или кооперативное действие.

Синергетика – совокупный коллективный эффект взаимодействия большого числа подсистем, приводящих к образованию устойчивых структур, т.е. самоорганизации в сложных системах.

Основным объектом изучения синергетики являются диссипативные структуры. Т.е. структуры, которые  могут существовать только при наличии интенсивного обмена с окружающей средой. Т.е. эти структуры живут за счёт своего окружения. Это динамические структуры.

2) Отличие подходов в кибернетике и синергетике.

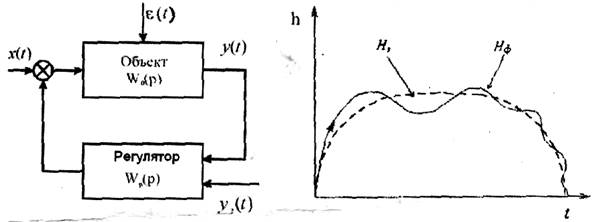
Если в кибернетике основное внимание уделяется роли рулевого (регулятора), то в синергетике основная задача заключается в выборе таких воздействий на систему, которые были бы согласованными с её внутренними свойствами. В кибернетических системах управления основной целью является стабилизация системы относительно заданного уровня или программного режима, в синергетике основной задачей является определение условий перехода системы в неустойчивое состояние, позволяющее вывести систему на более высокий структурный уровень.

3) Что такое диссипативная структура.

Диссипативная структура – структура, которая обменивается с окружающей средой веществом или энергией. Пример – обмен теплом, расширение газа расплывание капли чернил в воде, облака, ячейки бенара, популяция животных.

4) Что такое фрактал?

Термин фрактал происходит от греческого слова «fractus» - разбитый, расчлененный, дробный. Образуется путём бесконечного повторения исходной формулы во всё уменьшающемся масштабе по определённому закону, то есть это как бы самопроизвольная структура. Фрактальные структуры играют большую роль при изучении проблемы перехода от порядка к хаосу и наоборот.

z = z² +с.

5) Принцип порядка Больцмана.

Больцман сделал попытку описания вероятности для систем, состоящего из большого числа частиц.

S = K_BLnW, где S- энтропия, W - вероятность, число комплексов.

K_B = R/N_a= (8.31)/(6*10²³) = 1,38*10^-23Дж/К - универсальная постоянная Больцмана.

Из принципа Больцмана следует, что необратимое термодинамическое изменение есть приближения к более вероятным состояниям, и что состояние - аттрактор есть макроскопическое состояние, соответствующее максимуму вероятности. Как только такое состояние достигнуто, система отклоняется от него лишь на незначительное расстояние и на короткое время. Т.е. система флуктуирует около состояния аттрактора. Энтропия в равновесии = 1 максимуму.

6) Два принципа асимметрии природы на примерах преобразования энергии.

Внутренняя асимметрия - однонаправленность всех самопроизвольно протекающих в природе процессов. Горячие тела с течением времени охлаждаются, однако холодные сами по себе не становятся горячими, прыгающий мяч постепенно останавливается, однако самопроизвольно мяч не начинает прыгать.

Другой аспект асимметрии природы - преобразование теплоты в работу. Этот аспект природы позволяет не просто овладеть энергией, запасённой в топливе, но и извлечь из неё движущую силу, кт в свою очередь открывает возможность воздвигать искусственные сооружения, транспортные средства, поддерживать связь на расстоянии.

7) Соотношение взаимности Онсагера (связь между силами и потоками в линейной термодинамике).

q_t=λΔT

q_c=βΔC

Это соотношение определяет область линейной термодинамики.

Если систему можно описать такими линейными уравнениями, и существуют взаимные соотношения между этими процессами, заключающимися в том, что сила (1) действует на поток (2), в таком же соотношении как сила (2) на поток (1), то система линейна.

8) Теория о минимуме производства энтропии и вытекающие из нее выводы.

Открытая система dS = d_tS + d_eS

Для изолированной системы d_eS=0, то dS = d_iS≥0. При равновесии S = S_mm

Эволюция в открытой системе возможна, если dS =∫dS<0, то в системе возможно

образование упорядоченной структуры и в стационарном состоянии.

dS=0, a d_eS = -d_iS. Если d_iSи d_eS-> 0, то система стремиться к термодинамическому равновесию, т.е. к максимальном хаосу. S_равн=S_max. Для вывода уравнения используются три следующих уравнения:

1) Уравнение баланса массы:

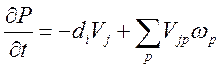
2) Дифференциальное соотношение Гиббса:

,

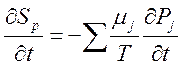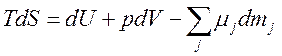
3) Уравнение баланса энтропии:

,

.

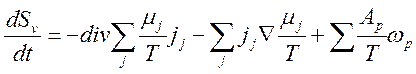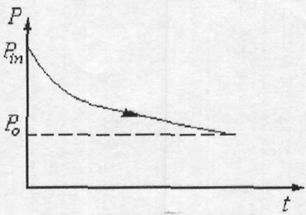
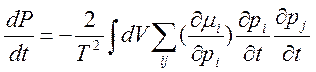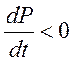 - вдали от стационарного состояния.

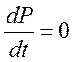 - в стационарном состоянии.

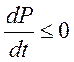- в общем случае.

В линейной системе, возникшие внутри системы или внесённые извне возмущения (флуктуации) асимптотически затухают.

По этому, самоорганизация, в смысле спонтанного образования новой, более высокоорганизованной структуры невозможна.

Систему текущего равновесия, можно рассчитывать теми же термодинамическим потенциалом, что и для равновесной термодинамики. Такие системы математически описываемые и предсказуемы.

9) Критерий эволюции.

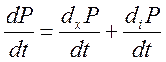, где 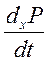- дестабилизация (химизм), - стабилизация (диффузия).

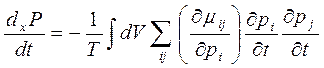
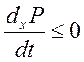- критерий эволюции.

В линейной области переходит в теорему о минимальном производстве энтропии.

10) Соотношение, связывающее условия термодинамической устойчивости с кинетикой химических реакций.

, ;

, ;

.

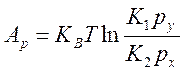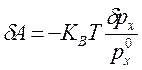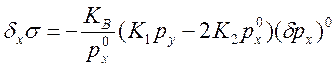11) Упрощенный механизм образования шестигранных ячеек в модели Бенара.

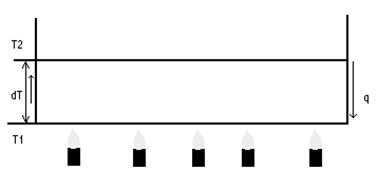
1)ΔT < ΔT_{критич.} – слабая конвекция.

2) ΔT = ΔT_критич – конвективная неустойчивость. Появляются ячейки Бенара.

3)дальнейшее повышение приводит к турбулентности.

12) Примеры решения задач нелинейной теплопроводности и их практическое применение.

Распространение тепла в цилиндре:

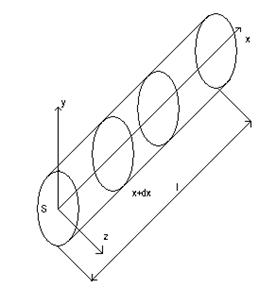
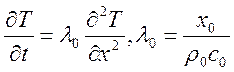
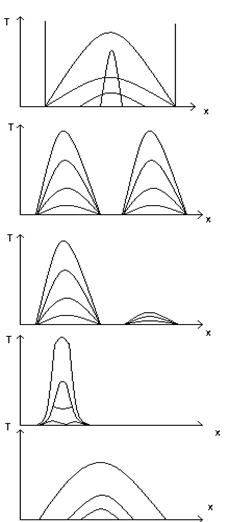
Тепло доходит до точек А и в и останавливается

Если 2 источника расположены далеко, то они будут развиваться независимо друг от друга.

Если 2 источника расположены близко, то один подавляет другого

В зависимости начальных параметров можно получить нужный режим распространения тепловых волн.

13) Составляющие энтропии в реакции окисления железа.

1) энтропии в окружающей среде;.

2) энтропии за счет уменьшения объема.;

14) Составляющие энтропии в реакции диссоциации.

А₂  2А

1) объема в следствии энтропии

2) энтропии за счет упорядочивания теплового движения молекул.

3) энтропии за счет числа частиц

4) энтропия смешения имеет максимум.

15) Что вы знаете о реакции Белоусова-Жаботинского.

Реакция Белоусова – Жаботинского является примером автокаталитической реакции. Реакция состоит в окислении органической кислоты в присутствии соответствующего катализатора – церия, или марганца. Визуально выражается в чередовании красных и сиих полос через строго определенное время. Это называется химическими часами.

16) Объяснение механизма самоорганизации мартеновской ванны с позиции теории самоорганизации.

По мере уваривания шлака и его гомогенизации уменьшается поверхность для зарождения пузырьков в подшлаковом слое (прекращается поверхностное кипение). Для достаточно интенсивного перехода в нижние слои металла и обеспечения зарождения и роста пузырей на подине должен возрасти градиент концентрации кислорода в металле по отношению к равновесному, а также градиент концентраций кислорода в шлаке по отношению к равновесному между шлаком и металлом.

17) Схема механизма колебательности в металлургическом реакторе-осцилляторе.

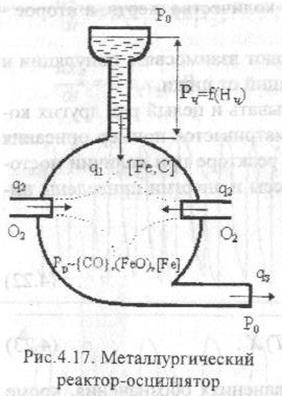
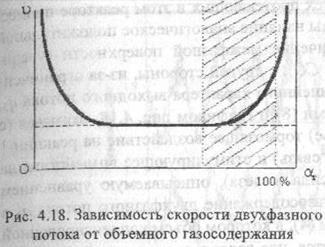
18) Принцип наименьшего принуждения.

При внешнем воздействии на систему, система в ответ вырабатывает действие направленное противодействие внешнего воздействия. Для доказательства используется уравнение .

19) Принцип подчинения.

Простейшее эволюционное уравнение:

,

В случае если вещество 1 с концентрацией q₁ образуется автокаталитически из вещества 2 с концентрацией q₂ то эволюционное уравнение для скорости образования вещества 1 имеет вид

Автокаталитические реакции, протекающие при определенных принудительных условиях, проявляют некоторые свойства живых систем:

обмен веществ - постоянное использование исходного сырья для создания новых химических соединений;

самопроизводство - способность вещества, размножаться за счет сырья;

отбор (селекция) - конкурентное поведение компонента в слу­чае ограничений, налагаемых на сырье или на общее количество имеющихся в распоряжении мест (концентраций), в конечном итоге остается тот компонент, который наиболее приспособлен.

20) Примеры микроосцилляторов в металлургии.

21) Соотношения для критического размера диффузионной области.

22) Отклонение от равновесия и бифуркации (бифуркационная диаграмма).

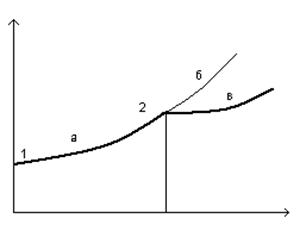
а) Близкие к равновесию стационарные состояния асимптотически устойчивы

б) После некоторого критического значения термодинамическая ветвь, может стать неустойчивой, при этом даже достаточно малое возмущение уводит систему с термодинамической ветви.

в) новый устойчивый режим может соответствовать упорядоченному состоянию

2 – точка бифуркации.

23) Роль флуктуаций в механизме самоорганизации.

Возникновение неустойчивости можно рассматривать как результат флуктуации которая была локализована в малой части системы, а затем распространилась и привела к новому макроскопическому состоянию, т.е. воздействие флуктуаций на систему может привести к ее упорядочиванию (самоорганизации).

24) уравнение динамики популяций животных за счет общего ресурса.

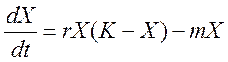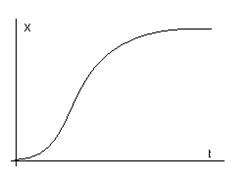
, где r и m – характерные постоянные рождаемости и смертности; K – ресурсы среды; X – численность популяций.

\

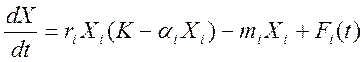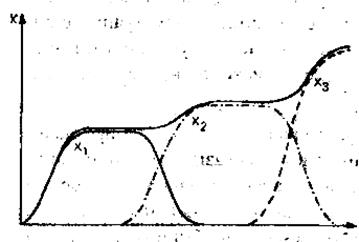
25) Уравнения популяций типа хищник-жертва.

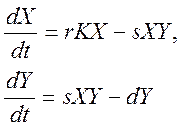
X – источник питания, Y - хищник

26) Вывод уравнения Ланжевена.

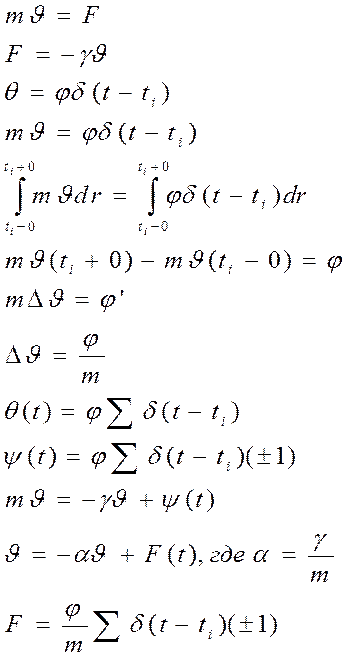
27) Вывод критерия эволюции с выходом на связь устойчивости с термодинамическими параметрами.