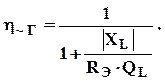
Обычно величина ![]() мало отличается от единицы и
потерями в Г-звене можно пренебречь. В противном случае влияние потерь в
Г-звене необходимо учесть при последующих
расчетах цепи согласования.
мало отличается от единицы и
потерями в Г-звене можно пренебречь. В противном случае влияние потерь в
Г-звене необходимо учесть при последующих
расчетах цепи согласования.
Трансформирующее Г-звено обладает небольшой фильтрующей способностью. Значение коэффициента фильтрации Г-звена можно рассчитать по формуле
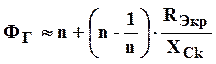 ,
,
где n – номер
гармоники. Поскольку обычно ![]() , величина
, величина ![]() незначительно превышает n
и может быть использована как запас по фильтрации всей цепи согласования ВУМ.
незначительно превышает n
и может быть использована как запас по фильтрации всей цепи согласования ВУМ.
4.2. Принципиальные схемы цепей согласования
Как говорилось выше, при коэффициенте перекрытия по
частоте ![]() цепи согласования ВУМ можно
выполнить в виде связанных резонансных контуров и работать в полосе их
пропускания без перестройки. Такая реализация ЦС ВУМ позволяет совместить
решение двух задач: задачу трансформации нагрузки и задачу фильтрации высших
гармоник. На рисунках, приведенных далее, представлены схемы ЦС для однотактных
и двухтактных схем ВУМ.
цепи согласования ВУМ можно
выполнить в виде связанных резонансных контуров и работать в полосе их
пропускания без перестройки. Такая реализация ЦС ВУМ позволяет совместить
решение двух задач: задачу трансформации нагрузки и задачу фильтрации высших
гармоник. На рисунках, приведенных далее, представлены схемы ЦС для однотактных
и двухтактных схем ВУМ.
При выборе варианта построения целесообразно выбирать схемы ЦС, которые обеспечивают выполнение поставленных перед ними задач по согласованию и фильтрации и в то же время наиболее просты в реализации.
На рис. 4.5 представлена ЦС в виде двух связанных параллельных контуров третьего вида, внешне напоминающая ФНЧ.
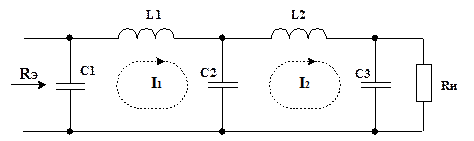
Рис. 4.5. ЦС в виде двух связанных параллельных контуров
Эта схема отличается повышенной фильтрующей способностью [6]. Коэффициент фильтрации такой цепи по n-й гармонике на частоте полного резонанса можно рассчитать по формуле
![]() ,
,
где ![]() - нагруженные
добротности первого и второго контуров. Значения нагруженных добротностей
связаны с добротностями контуров на холостом ходу соотношением
- нагруженные
добротности первого и второго контуров. Значения нагруженных добротностей
связаны с добротностями контуров на холостом ходу соотношением
![]() ,
,
где
![]() - КПД контура. Все другие виды
связанных контуров по фильтрующей способности уступают приведенной схеме.
Вместе с тем при низкоомных значениях
- КПД контура. Все другие виды
связанных контуров по фильтрующей способности уступают приведенной схеме.
Вместе с тем при низкоомных значениях ![]() и
и ![]() фильтрующая способность двух
связанных контуров может оказаться недостаточной. Тогда для получения
требуемого коэффициента фильтрации можно увеличить число связанных контуров
либо уменьшить коэффициенты включения сопротивления нагрузки и АЭ в контуры
путем использования в продольных цепях последовательных контуров, настроенных
на рабочую частоту (рис. 4.6):
фильтрующая способность двух
связанных контуров может оказаться недостаточной. Тогда для получения
требуемого коэффициента фильтрации можно увеличить число связанных контуров
либо уменьшить коэффициенты включения сопротивления нагрузки и АЭ в контуры
путем использования в продольных цепях последовательных контуров, настроенных
на рабочую частоту (рис. 4.6):
![]() .
.
После объединения индуктивностей ![]() и
и ![]() каждого
контура в одну индуктивность схема рис. 4.6 принимает вид, представленный на
рис. 4.7.
каждого
контура в одну индуктивность схема рис. 4.6 принимает вид, представленный на
рис. 4.7.
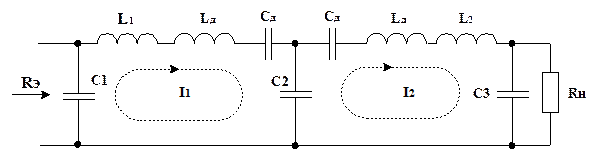 Рис. 4.6. Использование в ЦС
последовательных контуров
Рис. 4.6. Использование в ЦС
последовательных контуров
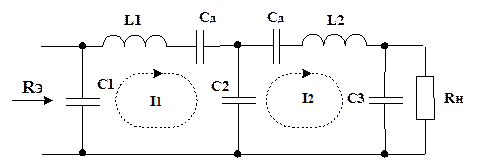
Рис. 4.7. Окончательный вид схемы по рис. 4.6
В схемах рис. 4.5-4.7 элементом связи между контурами служит емкость С2. Такой вид связи получил название внутриконтурной емкостной связи. Величина сопротивления связи
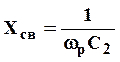 .
.
При расчетах полосы пропускания связанных контуров и их АЧХ возникает
необходимость рассчитать величину коэффициента связи ![]() между
контурами и фактор связи
между
контурами и фактор связи ![]() .
.
Величины ![]() и
и ![]() рассчитываются
по формулам
рассчитываются
по формулам
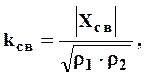
![]() ,
,
где ![]() волновые сопротивления первого и
второго контуров соответственно,
волновые сопротивления первого и
второго контуров соответственно, ![]() - нагруженные
добротности контуров.
- нагруженные
добротности контуров.
При факторе связи ![]() или близком к
единице АЧХ двух связанных контуров имеет уплощенную форму. Такая форма АЧХ
наиболее желательна при работе ЦС в диапазоне частот без перестройки.
или близком к
единице АЧХ двух связанных контуров имеет уплощенную форму. Такая форма АЧХ
наиболее желательна при работе ЦС в диапазоне частот без перестройки.
Иногда бывает удобнее использовать внешнеемкостную связь между
контурами. Такой вид связи может быть получен из схемы рис. 4.7
путем пересчета емкостей ![]() , соединенных
звездой, на емкости
, соединенных
звездой, на емкости ![]() , соединенные треугольником
(рис.4.8)
, соединенные треугольником
(рис.4.8)
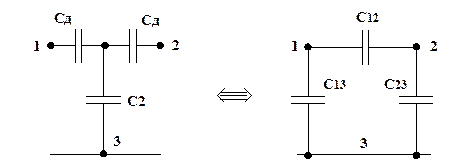
Рис. 4.8. Схемы «звезда» и «треугольник»
Формулы для пересчета емкостей из «звезды» в «треугольник»:
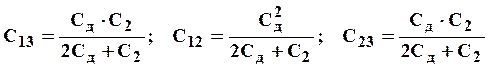 .
.
Преобразованная схема ЦС принимает вид, представленный на рис. 4.9.
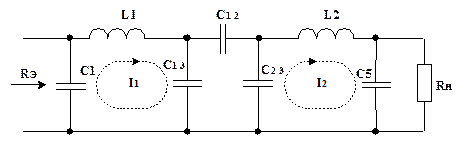
Рис. 4.9. Внешнеемкостная связь между контурами
Сопротивление связи между контурами в данном случае может быть рассчитано по формуле
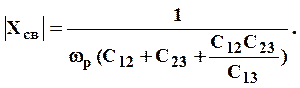
Рассмотренные виды ЦС наиболее целесообразно использовать в однотактных
ВУМ. В двухтактных ВУМ применение таких цепей согласования осложняется
необходимостью включения в состав ЦС симметрирующих устройств, например
симмертрирующего трансформатора. На рис. 4.10 представлена ЦС двухтактного ВУМ,
которая выполнена на основе схемы рис. 4.5 с симметрирующим трансформатором
типа ТДЛ. Достоинством двухтактных схем является способность подавлять в
оконечной нагрузке все четные гармоники: ![]() и
т. д. Кроме того, при работе АЭ ВУМ в классе «В» в токе выходного электрода
каждого плеча отсутствует третья гармоника
и
т. д. Кроме того, при работе АЭ ВУМ в классе «В» в токе выходного электрода
каждого плеча отсутствует третья гармоника ![]() .
.
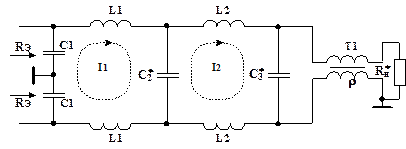
Рис. 4.10. ЦС для двухтактного каскада с ТДЛ
Степень подавления четных гармоник зависит от качества симметрии схемы. Наибольшее влияние на качество симметрии схемы оказывает разброс параметров АЭ. При подборе транзисторов степень ослабления второй и четвертой гармоник достигает (15…20) дБ. Налажен выпуск специальных балансных транзисторов [1], представляющих собой транзисторную микросборку с очень малым разбросом параметров. При использовании балансных транзисторов степень ослабления второй и четвертой гармоник может достигать 25 и более дБ.
Снижение уровня четных гармоник позволяет снизить требования к цепям согласования в двухтактных схемах по коэффициенту фильтрации в среднем на (15…20) дБ. Снижение требований по подавлению существенно упрощает схемы ЦС двухтактных ВУМ и позволяет использовать в них контуры с меньшей фильтрующей способностью.
На рис.4.11 представлен вариант построения ЦС двухтактного ВУМ с ВЧ трансформатором.
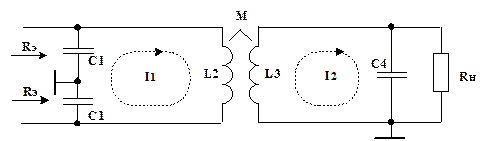
Рис. 4.11. ЦС для двухтактного каскада с трансформатором
Сопротивление связи между первым и вторым контурами определяется соотношением
![]() ,
,
где ![]() .
.
Коэффициент фильтрации такой ЦС на частоте полного резонанса меньше, чем в первой схеме [6]. Его можно оценить по формуле
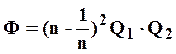 .
.
Если фильтрующая способность ЦС недостаточна, то, как и ранее, ее можно
увеличить путем включения последовательных контуров ![]() и
и
![]() , настроенных на частоту
, настроенных на частоту ![]() (рис. 4.12).
(рис. 4.12).
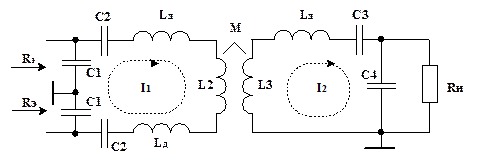
Рис. 4.12. ЦС с последовательными контурами
Включив ![]() в состав
в состав ![]() и
и ![]() и
пересчитав величину
и
пересчитав величину ![]() из условия
из условия
![]() ,
,
получим схему ЦС, представленную на рис. 4.13.
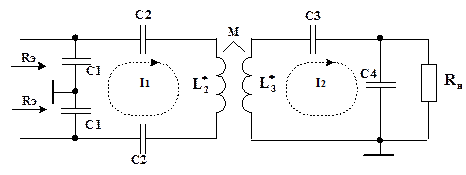
Рис. 4.13. ЦС с последовательными контурами
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.