Моделирование и модель. Основные этапы моделирования. Структурная схема познания объекта с помощью модели. Изоморфизмы и гомоморфизмы. Основные этапы структурной идентификации, страница 2

2.Слабая зависимость скорости от Т

3.Резкое влияние на скорость гидро- и аэродинамических условий процесса.

21. Признаки кинетического лимитирования гетерогенной реакции (c. 93)

1.Любой порядко реакции

2.Существует зависимость V от Т

3.Зависимость скорости от дисперсности

4.Отсутствует влияние на скорость гидро- и аэродинамических условий процесса

22. Уравнения теплопроводности для подвижной и неподвижной среды. (с.96)

Неподвижная среда:

, -тепловой поток (количество вещества, передаваемое через единицу поверхности в единицу времени), л-коэффициент теплопроводности

Подвижная среда (оказывает влияние свободная и вынужденная конвекция)

, где -теплоемкость при постоянном давлении

р-плотность среды, w-скорость потока, при Re<2300 или 2300<Re<10000

23. Уравнение теплопередачи излучением

-закон теплопереноса, где -коэффициент теплоотдачи, -разность температур.

, где -приведенная степень черноты, С₀-коэффициент лучеиспускания абсолютно черного тела, Т1 и Т2-температура 1 и 2ой поверхностей.

Чаще всего передача тепла теплопроводностью, конвекцией и излучением наблюдается одновременно:

, -общий коэф теплоотдачи, -коэф теплоотдачи соприкосновением и лучеиспусканием.

24. Допущения (постулаты) в методе наименьших квадратов. (c. 167-168)

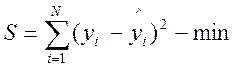
1.входные величины x1,...,xk должны измеряться с точностью, значительно превышающей точность измерения выходной величины у.

2.входные величины не должны быть коррелированны, т.е. статически связаны между собой.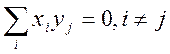

3.выходной параметр у есть случайная величина, подчиняющаяся нормальному закону распределения

4.дисперсия выходного параметра у не зависит от его абсолютной величины. Dy=const

25. Кодирование переменных и условия ортогональности при планировании эксперимента типа ПФЭ-2^к (c. 173-174)

Ни одной повторяющейся комбинации уровней, +1 и -1 – верхнее и нижнее значение фактора.

Значения кодированных переменных в столбцах произведений получают путем перемножения соответствующих переменных.

Условие ортогональности:

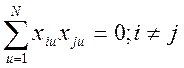. В следствие этого коэф уравнения регрессии определяются раздельно, независимо друг от друга и по очень простой формуле.

26. Формулы для  определения коэффициентов уравнения регрессии при эксперименте типа ПФЭ-2^к (c. 175-176)

Коэф bi при i-м факторе хi:

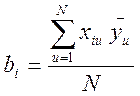, N-число вариантов опытов в матрице планирования, -значение кодированной переменной в u-й строке, u-го столбца, равное либо (-1), либо (+1).

-среднее значение выхода для u-го варианта опыта(строки).

Коэф при взаимодействии:

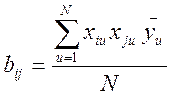, необходимо сложить построчные средние значения выхода с учетом знаков соответствующего столбца произведения.

Коэф b₀:

27. Критерии равноточности опытов (с. 179)

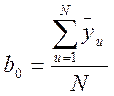
Критерий Кохрана

Построчные дисперсии:

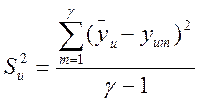,-число повторных опытов

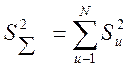- сумма построчных дисперсий

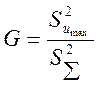, -максимальная из построчных дисперсий. Опыты равноточны если G<G_T, G_T-табличное значение критерия, выбираемое в зависимости от N,  и уровня значимости(надежности).

28. Критерии адекватности Фишера (с. 180)

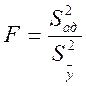, -усредненная дисперсия эксперимента, 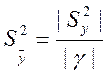 , -дисперсия адекватности, 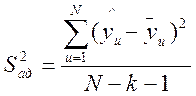, -рассчитанные по полученному уравнению значения выхода при значениях кодированных переменных, соответ каждой строке матрицы, -усредненные значения выхода, полученное при реализации повторных опытов для соот строки. Модель считается адекватной если F<Fтабл. Табличное значения критерия Фишера находят в зависимости от числа степеней свободы f1=(N-k-1) и f2=N(-1)

29. Формула для расчета АКФ (с.185-187)

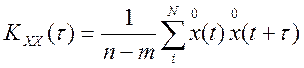, где 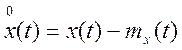- центрированное значение

30. Формула для расчета ВКФ

31. О каких свойствах объекта и каким образом можно судить по графикам АКФ и ВКФ
32. Уравнение статической динамики (Винера-Хопффа) и в чем заключается проблема некорректности (c.190)

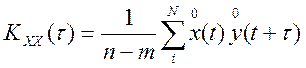
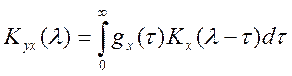, -весовая функция. Необходимость решения этого уравнения относительно , т.е. применение операции дифференцирования, приводит к некорректности этой задачи, заключающейся в том, что малые ошибки в определении корреляционных функций , приводят к большим ошибкам в определении g_x(t)

33. Схема упрощенного решения уравнений статической динамики методом неявных функций при интерактивном взаимодействии «ЭВМ» (c. 191)

34. Схема идентификации объекта методом подстраиваемой модели (c. 195)

35. Типовые графики при содержательном анализе остатков (c.201-203)

36. Классификация моделей в зависимости от свойств объектов (с. 204)

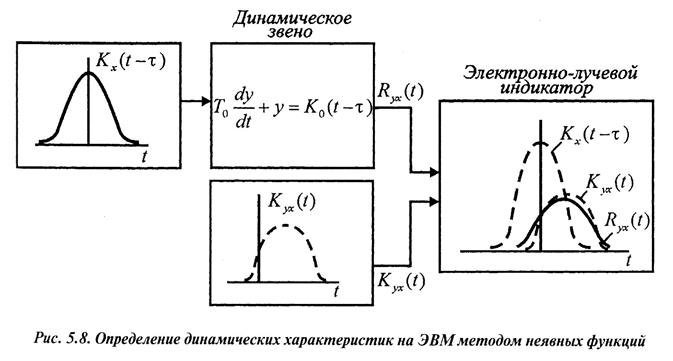
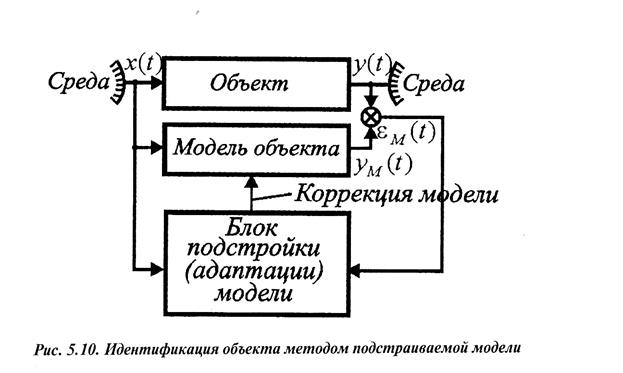
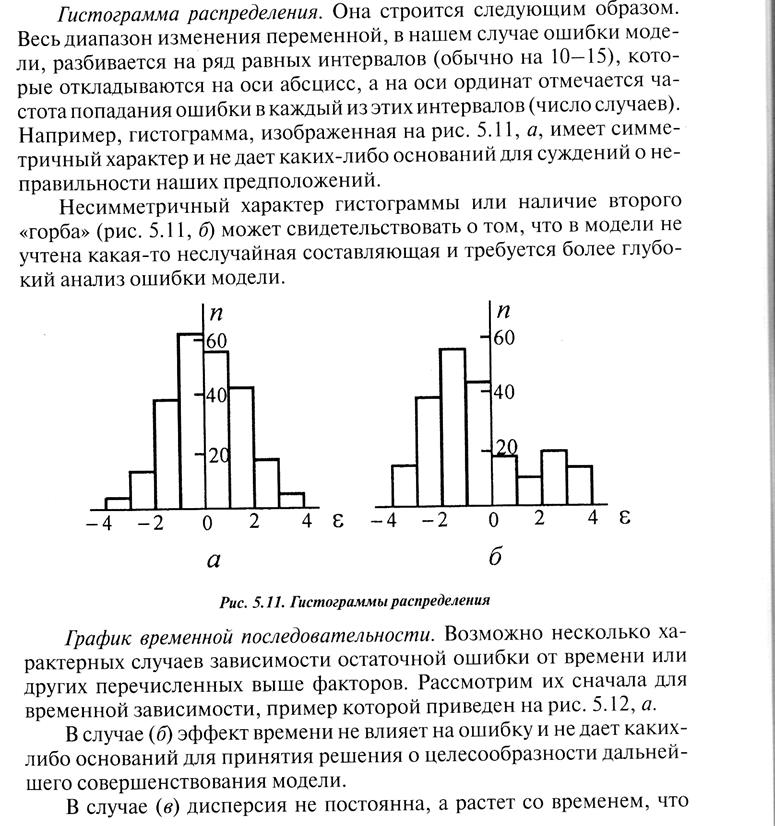
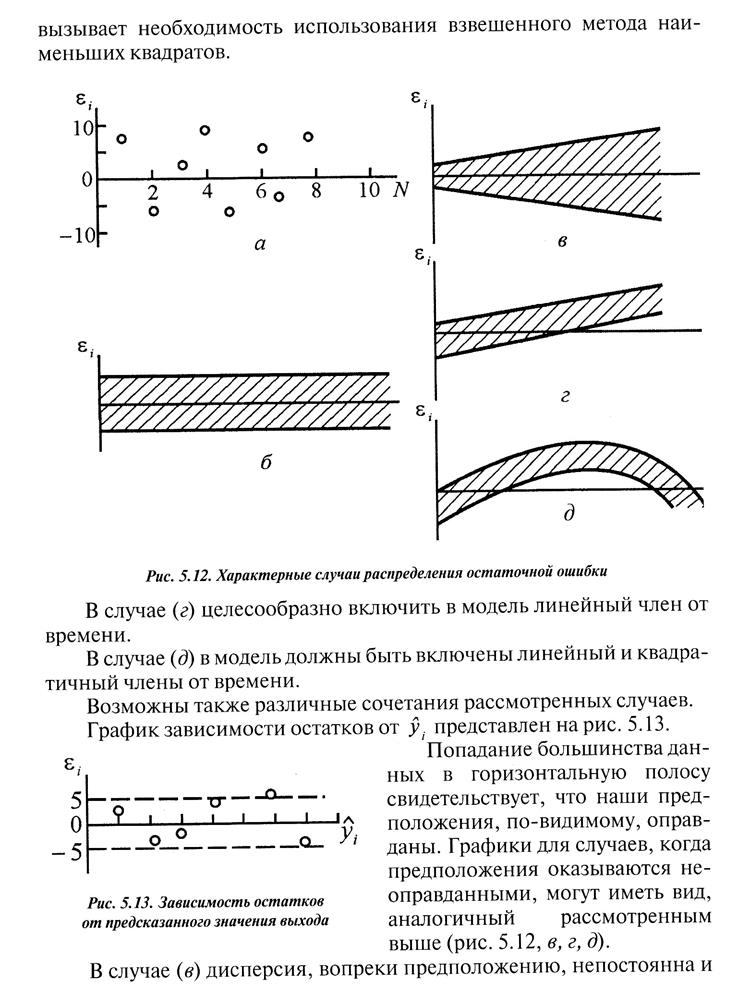
1.Статические и динамические

2.Детерминированные и стохастические

3.Линейные и нелинейные

4.Непрерывные и дискретные.

37. Каким видом уравнений описывается статический дискретный линейный детерминированный объект и сколько опытов нужно для его идентификации

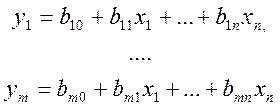
Y=B₀+BX. Необходимо m(n+1) опытов.

38. Алгоритм(уравнение) адаптивного шагового метода

, J-алгоритм оптимизации

 - метод наискорейшего спуска, где -невязка j-м шаге при значении параметра на (j-1)-м шаге адаптации

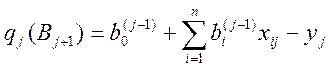
-истинное значение настроич коэф которое сводит на мин ошибку при каждом шаге.

39. Как зависит выбор настроечного параметра а и уровня помех. Показать на качественном уровне на графике процесс сходимости коэффициентов при разном значении а и уровне помех.
40. Алгоритмы автоматической подстройки моделей Челюскина А.Б и Райбмана Н.С. (с. 195-196).

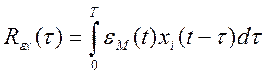непрерывный расчет взаимной корреляционной функции. Стремление к нулю свидетельствует об ослаблении влияния на ошибку модели данного входного параметра. Следовательно,

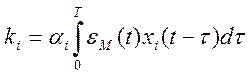, -коэф, характеризующий интенсивность самонастройки. Изменяем  пока коэф корреляции не будет в диапазоне , -зона нечувствительности по ошибке модели

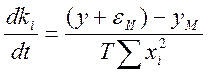, где - ошибка измерения выходной величины y_м-значение выходного параметра, получаемое на модели, Т-постоянная времени в контуре самонастройки. Для сходимости алгоритма ошибка предсказания должна удовлетворять условию

41. Основные этапы структурной идентификации (с. 197)

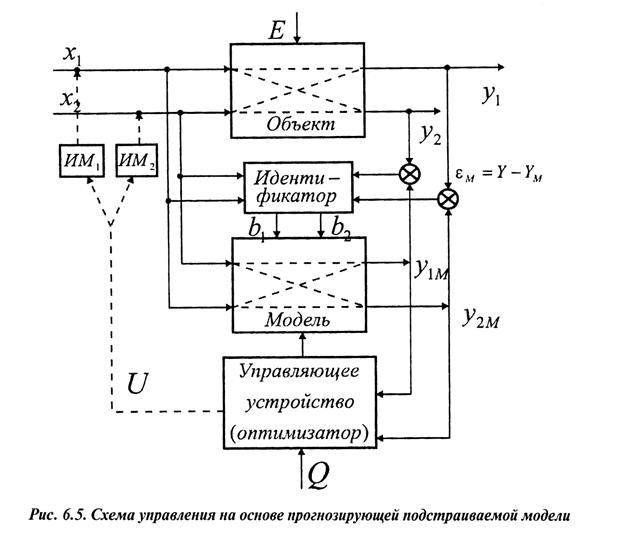
1.  Выделение объекта из среды

2.  Ранжирование входов и выходов по степени влияния

3.  Определение рационального числа входов и выходов

4.  Определение характеров связи между входом и выходом, т.к. этап структуризации

42. Структурная схема управления объектом на основе прогнозирующей подстраиваемой модели. (С.244)