Описание макромодели генератора управляемого напряжением, страница 2

.Define VP 1

.Define F0 1e3

.Define KF 1e3

.Define Funct1 VP*COS(2*PI*(F0*T+KF*v(VMOD)))

Видно, что сначала определяются значения параметров макромодели, а затем уже непосредственно самой функции Funct1. v(VMOD) – текущее значение напряжения в точке VMOD, которая является выходом интегратора.

Работа схемы иллюстрируется временными диаграммами, приведёнными на рисунке 3.

Рисунок 3. Временные диаграммы, иллюстрирующие работу макромодели ГУНа.

Верхняя диаграмма отображает сигнал на входе макромодели, средняя – выходной сигнал, нижняя – входной сигнал, прошедший интегратор.

Заметим, что текущая фаза выходных колебаний определяется как:

2*PI*(F0*T+KF*v(VMOD))

Или иначе:

2*PI*F0*T+2*PI*KF*v(VMOD)

Также отметим и то, что частота является производной фазы (скорости изменения фазы). В итоге получается так, что в те моменты времени, когда напряжение на входе макромодели равно нулю, напряжение на выходе интегратора имеет постоянное значение, и, умножаясь на крутизну модуляционной характеристики, прибавляет к текущей фазе какое-то конечное значение. Приращение же фазы во времени происходит только благодаря  2*PI*F0*Т (первому слагаемому), скорость приращения (частота) в такие моменты времени равна 2*PI*F0 (в смысле, циклическая частота).

В моменты же времени, когда напряжение на входе макромодели положительно и не изменяется, напряжение на выходе интегратора увеличивается по линейному закону, и, умножаясь на крутизну модуляционной характеристики, прибавляет к текущей фазе не какое-то конечное значение, а значение, которое также увеличивается с течением времени. Приращение фазы  теперь происходит не только благодаря 2*PI*F0*Т, но и благодаря  второму слагаемому. Следовательно, в данном случае скорость изменения фазы во времени (частота) больше, чем в те моменты времени, когда напряжение на входе макромодели равно нулю.

Диаграммы на рисунке 3 подтверждают всё вышеизложенное.

Необходимо также отметить, что, применяя подобный подход, можно объяснить работу макромодели ГУНа и при подаче на её вход других сигналов.

Следующим этапом анализа макромодели является построение спектра выходного сигнала макромодели, а также его АКФ (рисунок 4).

Рисунок 4. Выходной сигнал макромодели ГУНа во временной области, его спектр и АКФ, вычисленные в Micro-Cap.

Для правильного построения АКФ, в Micro-Cap необходимо указывать длительность времени анализа в несколько (хотя бы в два) раз больше длительности исследуемого сигнала. Далее, для наглядности представления, можно должным образом скорректировать пределы отображения.

Далее, для сравнения, сигнал с ЧМн был воссоздан в среде Matlab 6.5. На рисунках 5 и 6 представлены временные и спектральные диаграммы соответственно. Все значения параметров сигнала сохранены прежними.

Рисунок 5. Представление сигнала с ЧМн во временной области в среде Matlab 6.5.

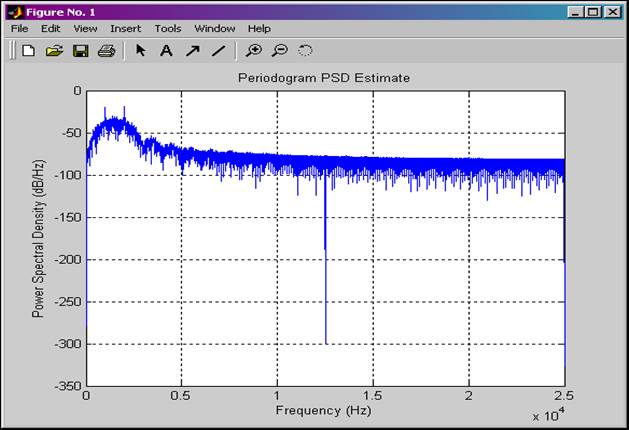
Рисунок 6. Спектр сигнала с ЧМн, построенный в Matlab 6.5.

Сопоставляя спектры с рисунков 4 и 6, можно прийти к выводу, что, в принципе они похожи. На обоих рисунках видны боковые полосы (верхняя и нижняя). Разница состоит лишь в том, что на спектре, полученном в Micro-Cap наблюдается наличие спектральной составляющей с частотой несущей, причём, её уровень даже выше уровня боковых полос. В спектре же сигнала ЧМн, построенном в Matlab несущая также есть, но её уровень значительно меньше уровня боковых полос, и это обстоятельство даёт более верное представление о сигнале [1].