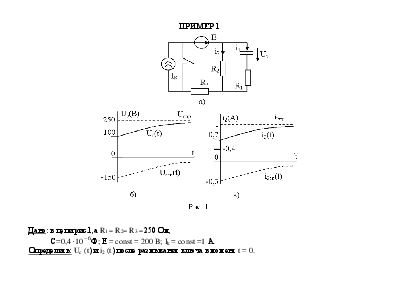
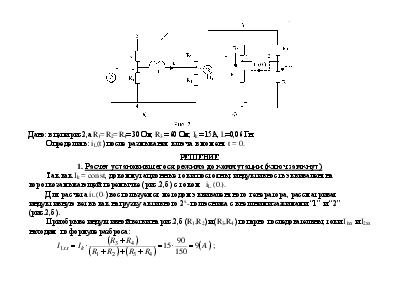
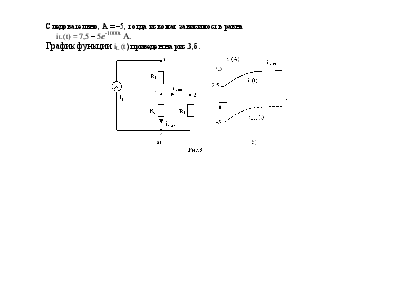
Пример 1
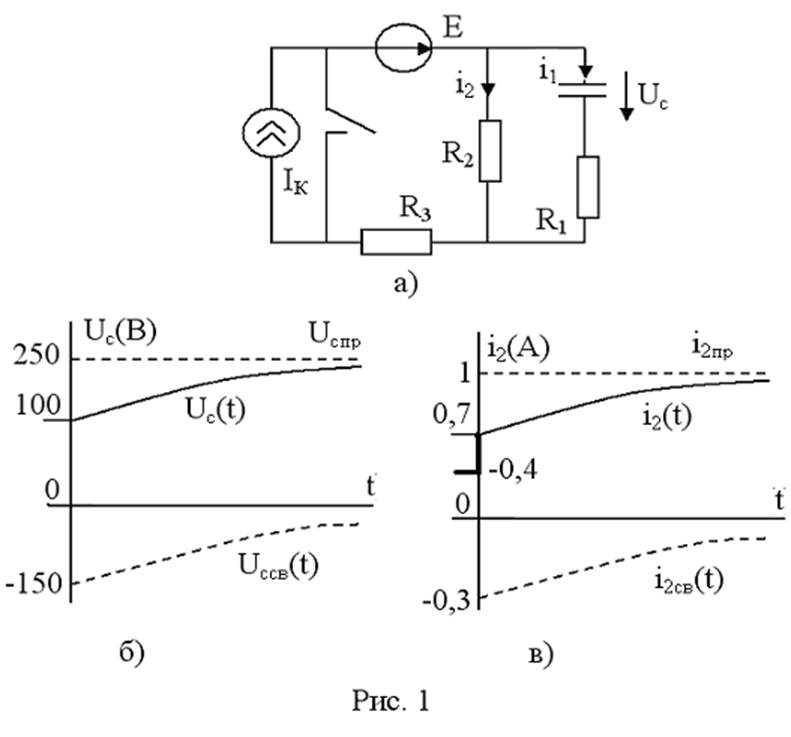
Дано: в цепи рис.1,а R1 = R2= R3 = 250 Ом,
С=0,4 
Ф; Е = const = 200 B; Ik = const =1 А.
Определить: Uc (t) и i2 (t) после размыкания ключа в момент t = 0.
Решение
1. До коммутации (ключ замкнут).
В установившемся режиме под действием постоянного источника э.д.с. ток через конденсатор не течет, поэтому
i1 (0_) = 0; i2 (0_) = i3 (0_) = E/(R1+R3);
Uc (0_) = i2
(0_)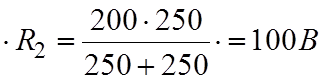 
.
2. Новый установившийся режим – принужденный (теоретически для 
).
i2пр
= Ik = 1A; Uспр =
i2пр
.
3.Характеристическое уравнение записываем по комплексному входному сопротивлению относительно емкостной ветви послекоммутационной цепи (с учетом бесконечно большого внутреннего сопротивления источника тока):
Z(p) =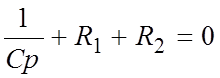 
.
Его решение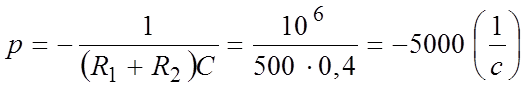 
позволяет записать в общем виде свободные составляющие искомых функций:
Uc св(t) = Aept = Ae-5000t B,
i2 св (t) = Bept = Be-5000t A.
4. Расчет постоянных А и B
Uc
(t) = Uспр + Uc св = 250 + Aept
i2(t) = i2пр + i2 св = 1 + Bept .
Для первого мгновения после коммутации:
Uc (0+) = 250 +А,
i2 (0+) = 1 + В.
Начальные значения Uc (0+) и i2 (0+) находим из физических соображений, учитывая 2ой закон коммутации
Uc (0+)
= Uc (0-)
= 100 В
и законы Кирхгофа для t = 0+:
i2 (0+) + i1 (0+) = Ik,
Uc (0+) + i1 (0+)
(0+)R2 = 0.
Решаем эти уравнения относительно i2 (0+),
i2
(0+) =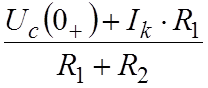 
= 0,7 А.
Итак, для постоянных имеем уравнения:
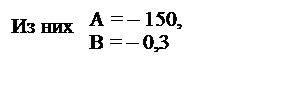
Uc (0+)
= 250 +А = Uc (0-)
=100;
i2 (0+) = 1+ В = 0,7.
Искомые зависимости:
Uc (t) = 250 – 150 e-5000t B.
i2 (t) = 1 – 0,3 e-5000t A.
Их графики построены на рис.1,б и рис.1,в.
Пример 2
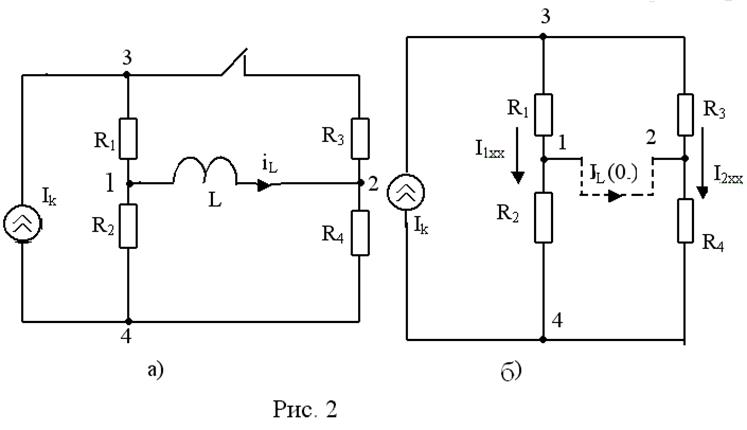
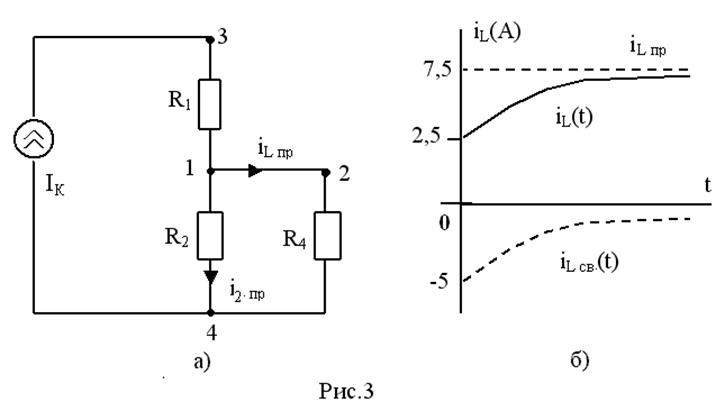
Дано: в цепи рис.2,а R1= R2= R4= 30 Ом; R3 = 60 Ом; Ik = 15А, L=0,06 Гн.
Определить: iL(t) после размыкания ключа в момент t = 0.
Решение
1. Расчет установившегося режима до коммутации (ключ замкнут)
Так как Ik = const, докоммутационные токи постояны, индуктивность эквивалентна короткозамыкающей перемычке (рис.2,б) с током iL (0-).
Для расчета iL (0-) воспользуемся методом эквивалентного генератора, рассматривая индуктивную ветвь как нагрузку активного 2х-полюсника с внешними зажимами “1” и “2” (рис.2,б).
При обрыве индуктивной ветви на рис.2,б (R1,R2) и (R3,R4) попарно последовательны, токи I1xx и I2xx находим по формуле разброса:
;
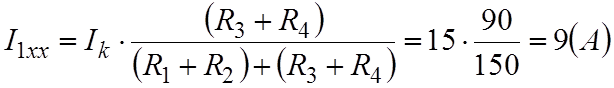I2xx = Ik – I1xx = 6(A).
Пусть 
, тогда для режима холостого хода
цепи рис.2,б
,
,
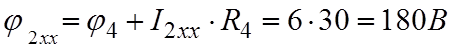Uxx12
=
.
Входное сопротивление активного 2х-полюсника относительно зажимов “1” и “2” записываем, учитывая бесконечно большое внутреннее сопротивление источника тока (обрываем ветвь с Ik):
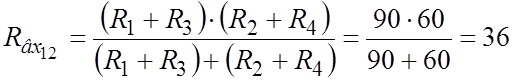Ом.
Ток в индуктивной ветви рис.2,б
iL (0-) =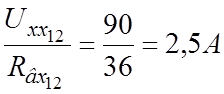 
.
2. Расчет принужденного режима (нового установившегося; ключ разомкнут)
При t
справедлива схема рис. 3,а.
Так как R2 = R4,
то в цепи рис. 3,а iLпр = i2пр = iк/2
=7,5 А.
3. Характеристическое уравнение (по комплексному входному сопротивлению относительно индуктивной ветви схемы рис.2,а при разомкнутом ключе) имеет вид:
; 
.
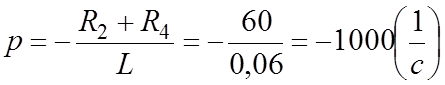При одном корне общий вид свободной составляющей индуктивного тока
iL св(t) = Aept = Ae-1000t.
4. Расчет постоянной А
iL (t) = iL пр + iL св = 7,5 + Aept ;
iL (0+) = 7,5 + А = iL (0-) = 2,5 А (по 1му закону коммутации).
Следовательно, А = –5, тогда искомая зависимость равна
iL (t) = 7,5 – 5e-1000t A.
График функции iL (t) приведен на рис.3,б.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.