Анализ свойств временного ряда (Первичный анализ временного ряда. Вторичный анализ стохастической составляющей), страница 2

Стьюдента (m,s)             0           Хи-квадрат (M)        2.04775594e-05 

Хи-квадрат (M)              0           Равномерное на [0,A]       0              

Гамма  (A,B)                0           Экспоненциальное (A)       0              

Равномерное на [0,A]        0           Стьюдента (m,s)            0              

Экспоненциальное (A)        0           Лапласа (A)                0              

Парето (A,B)                0           Парето (A,B)               0              

Лог.Нормальное (A,B)        0           Лог.Нормальное (A,B)       0              

Равномерное на [A,B]        0           Равномерное на [A,B]       0

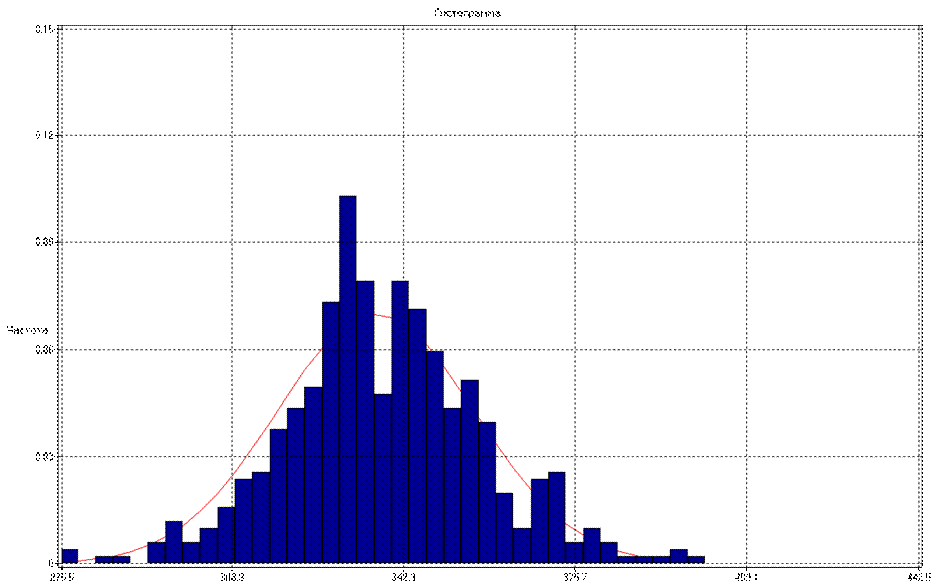
Согласно обоим критериям исследуемый вид распределения следует отнести к нормальному. Оценка функции плотности распределения имеет вид:

Непараметрический анализ корреляционных свойств временного ряда

Сглаженная оценка функции автокорреляции имеет вид:

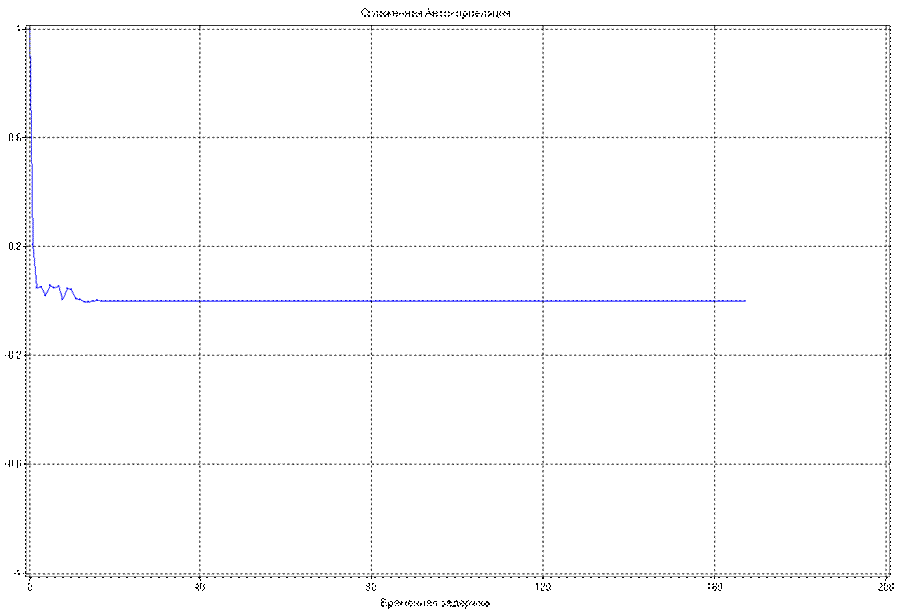
Полученная оценка является затухающей с параметром = 8.

Непараметрический анализ спектральных свойств временного ряда.

Оценка функции спектральной плотности в виде простой периодограммы имеет вид:

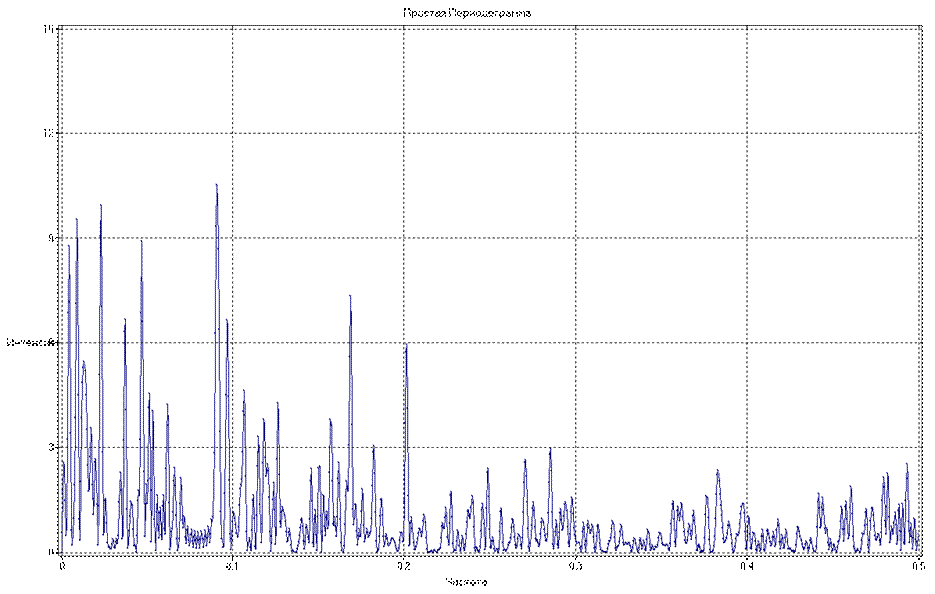
Данная оценка обладает большой дисперсией, и судить по ней о частотном составе процесса затруднительно. Однако можно заметить, что мощность низкочастотных составляющих преобладает над мощностью высокочастотных составляющих, где, по всей видимости, имеется провал.

Сглаженная оценка функции спектральной плотности мощности имеет вид:

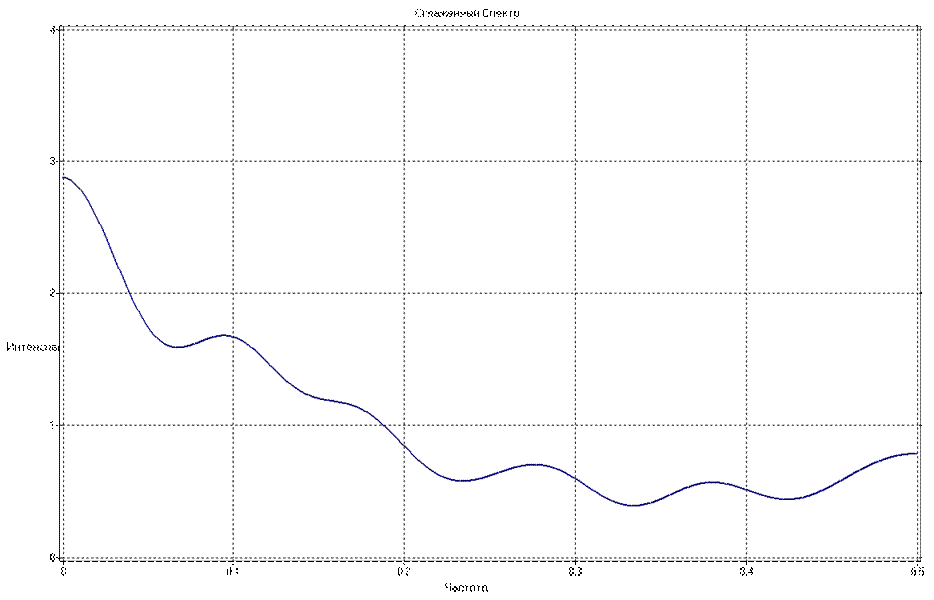
Получены результаты, позволяющие подтвердить сделанный ранее вывод. Основная мощность сигнала передается на низких частотах.

Расчет линейной стационарной стохастической модели временного ряда, включающий оценивание порядка и параметров модели, включающий анализ типа модели, порядка модели и оценивание параметров модели.

Оценки автокорреляционной функции и частной автокорреляционной функции имеют вид:

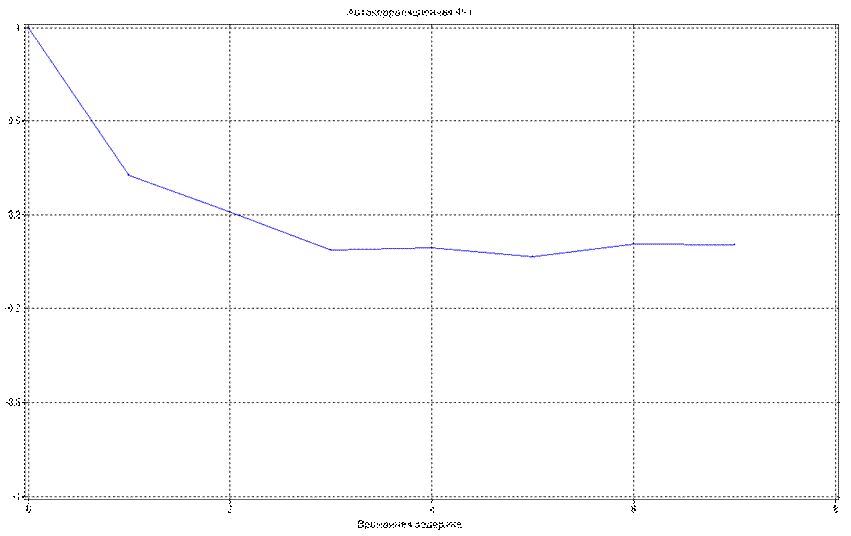
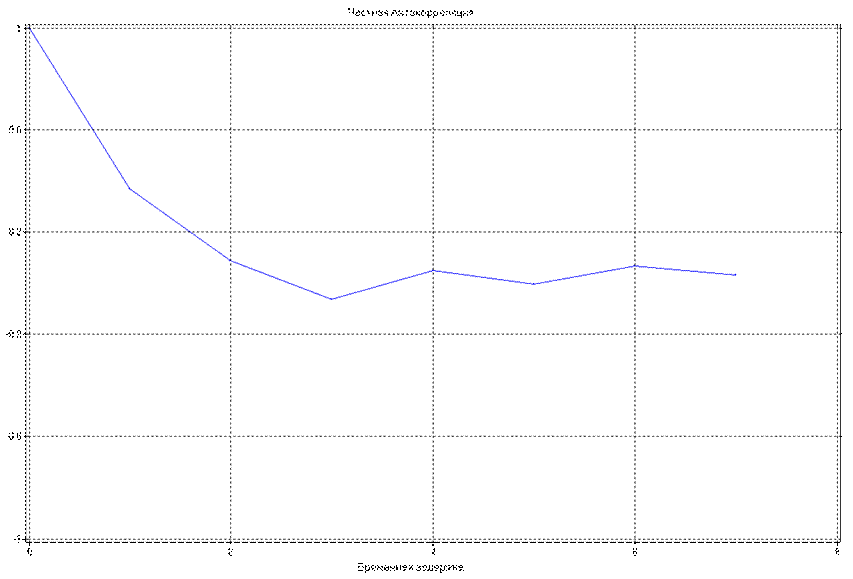
Анализируя внешний вид этих функции, можно сделать предположение, что ряд наилучшим образом можно описать с помощью АРСС модели.

Оценивание порядка и параметров модели дает следующие результаты:

          Параметры АРСС Модели

  Параметр  Оценка          Станд.Ошибка     T-Значение       P-Значение

 АР(1) =   -0.5352399271    0.09593782188    5.579029382      4.824764566e-08 

 СС(1) =   -0.1891140863    0.1114837835     1.696337174      0.04584824193   

          Дисперсия Остатков =305.3543369     

          Сумма кв. Остатков =153593.2315     

          Хи-Квадрат Тест автокорреляции Остатков =264.9794952      

             с числом степеней свободы = 166             

          Остатки есть Белый Шум с вероятностью не более чем =1.681888904e-06

Т.к. вероятность того, что остатки являются белым шумом довольно мала, то полученную оценку нельзя считать достаточно достоверной, но с ее помощью можно грубо описать поведение ряда.

Расчет линейной нестационарной стохастической модели (АРПСС) временного ряда, если это возможно.

АРПСС модель для исследуемого стационарного фрагмента ряда уже была оценена и имеет вид (1, 0, 1).

АРПСС модель может быть построена для нестационарного ряда с исключенной из анализа сезонной компонентой. Для этого ряда порядок дифференцирования, необходимый для того, чтобы превратить ряд в стационарный, можно найти из условия минимума СКО разностей различных порядков. Вычисляя указанные характеристики для исследуемого ряда можно получить следующие результаты:

Порядок разности	0	1	2	3
СКО	38.08108321	27.25007881	36.22732925	63.78953603

Т. о. искомый порядок разности равен 1. Для определения порядков и параметров АРСС модели разности первого порядка можно воспользоваться соответствующими критериями:

           Критерии порядка АР   - модели

                      АР-Порядок      Статистики

  Парзен                10            -1.863192511    

  Акаике (инф)          10            -0.6142444602   

  Акаике (ср.знач.)     10            0.5410532542    

  Хэннан-Куин           10            -0.6216008463   

           Критерии порядка АРCC - модели

            АР-Порядок   CC - Порядок  Статистика

              10          0           3010.664341                

Т. о. ряд можно описать АР моделью 10 порядка. Оценки ее параметров приведены далее:

           Дисперсия АР-Шума =385.4032187     

           (Дисперсия Шума ) / (Дисперсия Ряда) =0.5179850922    

  Параметр  Оценка          Станд.Ошибка     T-Значение       P-Значение

 АР(1) =   0.3996875683     0.0435842491     9.170458974      2.220446049e-16 

 АР(2) =   0.2145821771     0.04346864185    4.936482209      5.444778968e-07 

 АР(3) =   0.3157010809     0.04172465834    7.566295172      9.492406861e-14 

 АР(4) =   0.3261854419     0.03990866348    8.173299064      1.443289932e-15 

 АР(5) =   0.4182411776     0.03817966491    10.95455339      0               

 АР(6) =   0.4178269014     0.03817966491    10.94370268      0               

 АР(7) =   0.4177693709     0.03990866348    10.46813735      1.110223025e-16 

 АР(8) =   0.3479601191     0.04172465834    8.33943603       3.330669074e-16 

 АР(9) =   0.4059956216     0.04346864185    9.339965648      2.220446049e-16 

 АР(10) =  0.2017639248     0.0435842491     4.629285325      2.347010281e-06 

          Сумма кв. Остатков =175860.449      

          Хи-Квадрат Тест автокорреляции Остатков =18.75887237     

             с числом степеней свободы = 12              

          Остатки есть Белый Шум с вероятностью не более чем =0.0945161038

Подводя итог, можно сказать, что исходный ряд может быть описан нестационарной АРПСС (10, 1, 0) моделью.

Расчет  параметрических оценок корреляционной функции и спектральной плотности мощности,

Параметрическая оценка АКФ, полученная по рассчитанным параметрам имеет вид:

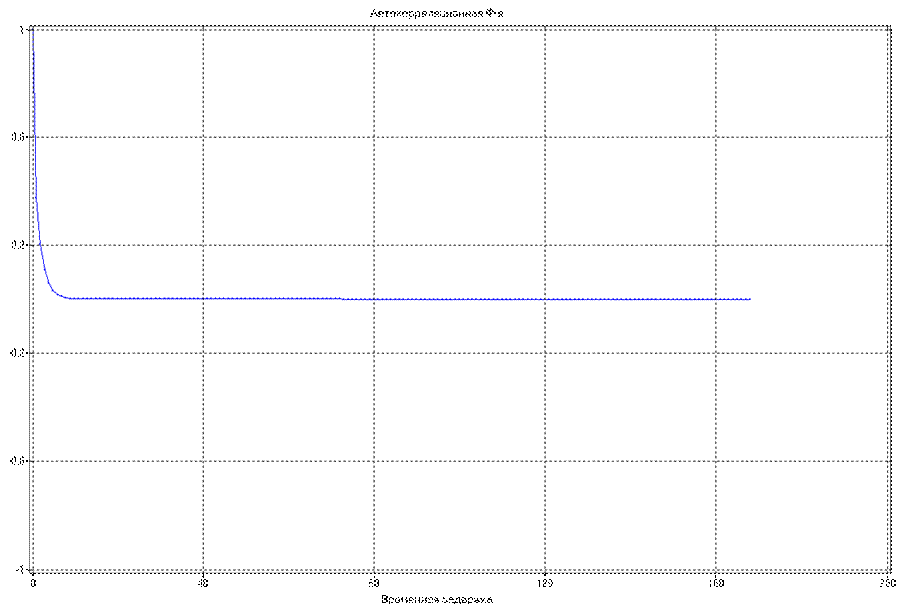
Параметрическая оценка СПМ, полученная по рассчитанным параметрам имеет вид:

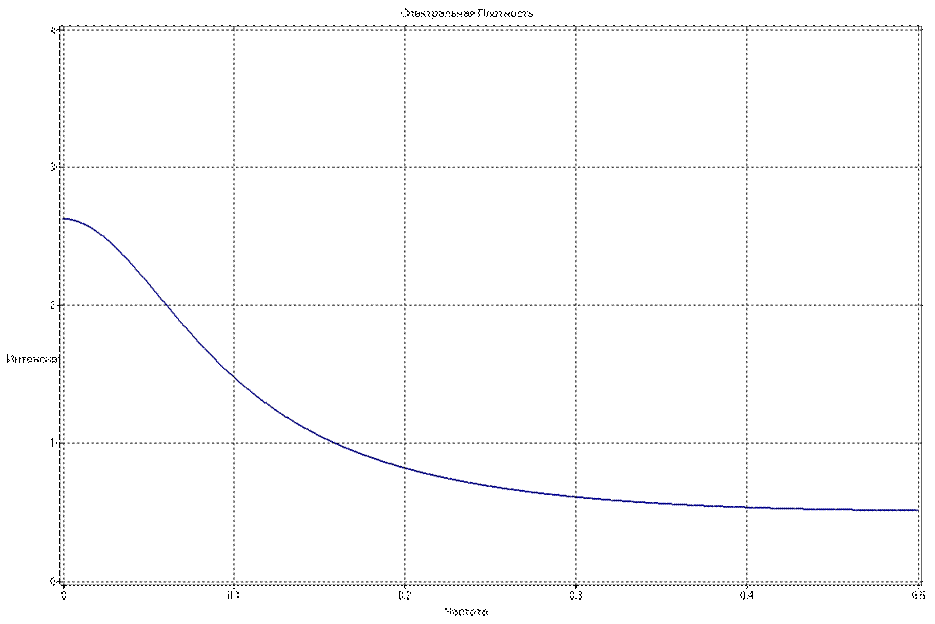
Получаемые в результате непараметрического оценивания по ряду наблюдений, полученных с помощью найденной АРСС модели, характеристики могут существенно искажаться в сравнении с представленными характеристиками, но будут к ним стремиться.

Сравнение результатов параметрического и непараметрического оценивания корреляционной функции и спектральной плотности мощности.

Сравнивая результаты параметрического и непараметрического оценивания АКФ можно заметить, что параметрическая оценка в целом повторяет характер непараметрической оценки:

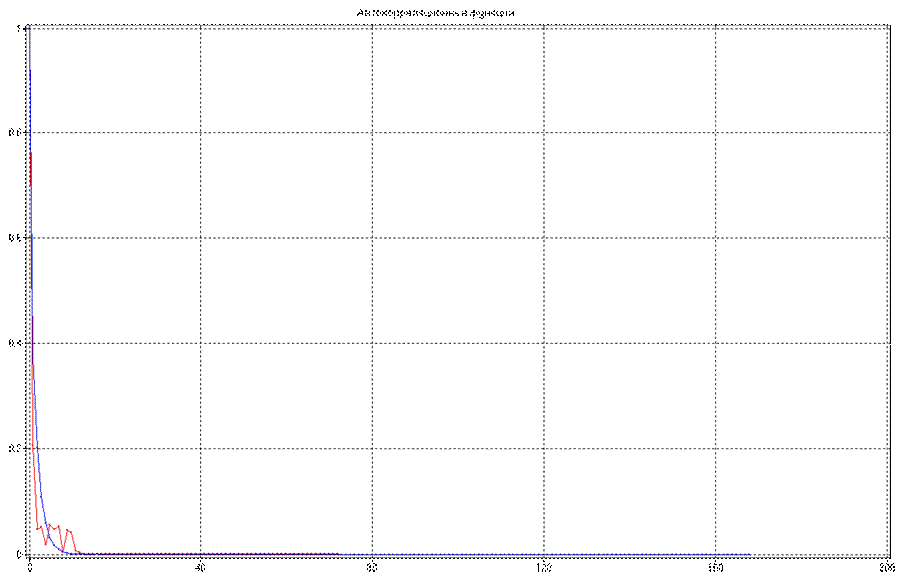
Сравнивая результаты параметрического и непараметрического оценивания функции СПМ можно заметить, что параметрическая оценка в целом повторяет характер непараметрической оценки, но содержит меньшее количество гармоник и является более сглаженной:

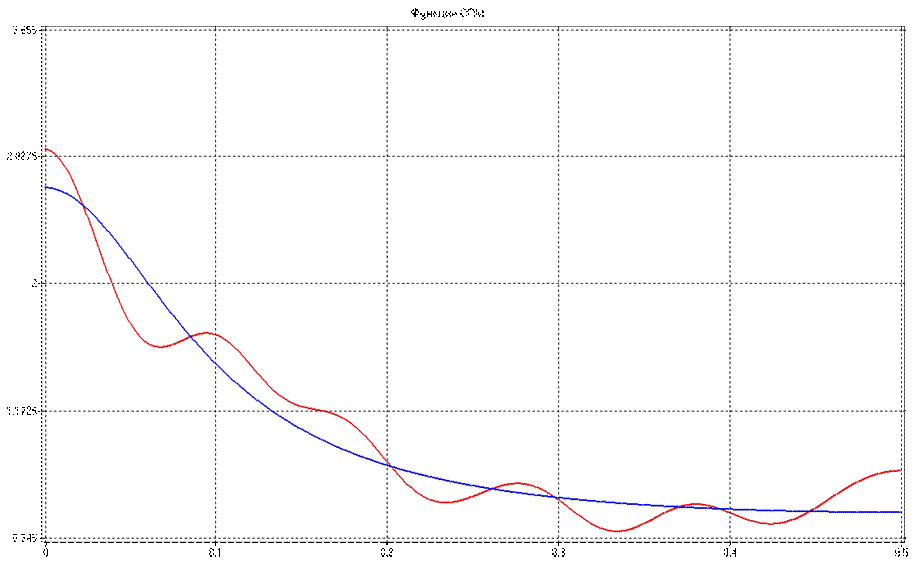
Т.о. полученную АРСС модель можно считать вполне адекватной.