Счетчики электрической энергии переменного тока, страница 4

Теоретические сведения

На рисунке 3.2 изображено направление силовых линий (поток Ф_I) в проводнике, по которому проходит ток I при подаче напряжения U.

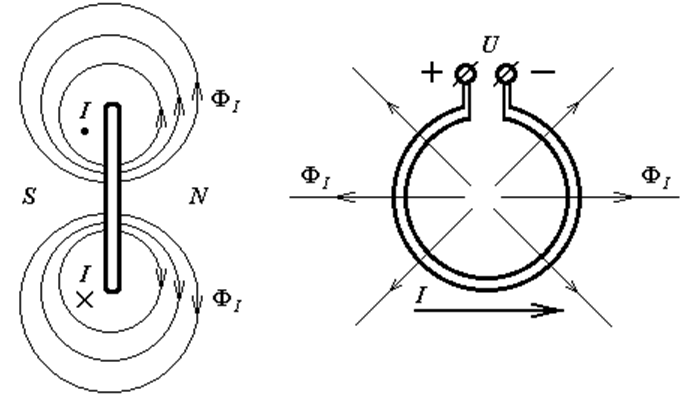Рис. 3.2 Электромагнит

 Крестиком обозначено направление протекания тока в плоскость рисунка, точкой – в противоположную сторону. На рисунке 3.3 изображены ток в контуре (а) и сила, действующая на проводник с током в поле постоянного магнита (б). Согласно рис. 3.2, электромагнит отталкивает подносимый к нему постоянный магнит, который вызвал появление тока в контуре (рис. 3.3, а.) Силовые линии поля проводника с протекающим током (рис. 3.3, б) выталкивают силовые линии поля постоянного магнита в область, где их направление совпадает. Большая концентрация силовых линий приводит к появлению силы, действующей на проводник с током.

Рис. 3.3 Взаимодействие потоков и токов:

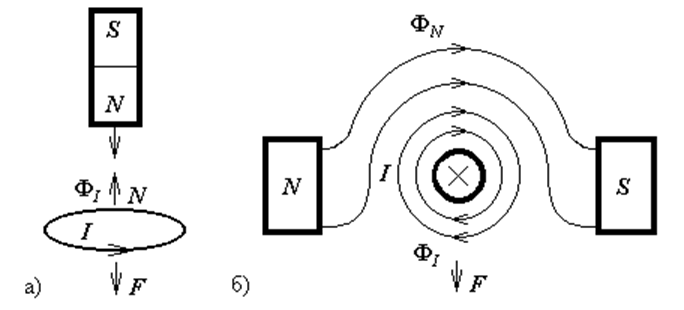а – направление индуцированных токов в контуре;

б – направление силы, действующей на проводник с током.

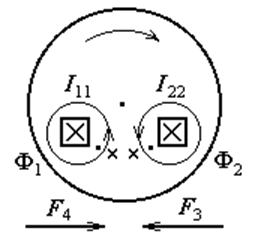
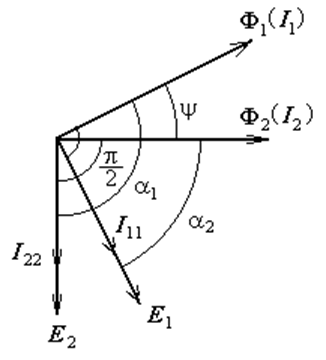
На рисунках 3.4 и 3.5 (с учётом рис. 3.3) изображены направления потоков Ф₁, Ф₂ и индуцированных ими токов I₁₁, I₂₂ в диске счётчика, а также их векторные соотношения соответственно. Направление потоков в плоскость рисунка выбрано за положительное при дальнейшем анализе.

Рис. 3.4. Направление потоков                  Рис. 3.5. Векторная диаграмма

                                       и токов в диске

Из рис. 3.4. следует, что поток Ф₁ притягивает ток I₂₂, индуцированный потоком Ф₂ (сила F₃), а поток Ф₂ – ток I₁₁ (сила F₄).

Для вращения диска счётчика необходимо наличие не менее двух потоков, разнесённых в пространстве.

Мгновенное значение силы взаимодействия тока iи потока Ф_t равно:

F_t = ciФ_t ,

где с – коэффициент пропорциональности.

Если Ф_t = Ф_m sin ωt; а i = I_m sin (ωt – α), то F_t = cI_m Ф_m sin ωt ·sin (ωt – α).

Среднее значение силы за период:

F = cI Ф cos α.

Среднее значение силы взаимодействия потоков Ф₁, Ф₂ и индуцированных ими токов I ₁₁, I ₂₂ соответственно за период (рис. 3.3, а)

F₁ = c₁ I ₁₁ Ф₁ cos (π/2) = 0;  F₂ = c₂ I ₂₂ Ф₂ cos (π/2) = 0,

где c₁ и c₂ – постоянные коэффициенты.

Среднее значение силы при взаимодействии Ф₁ и I ₂₂:

             F₃ = c₃ I ₂₂ Ф₁ cos α ₁ = c₃ I ₂₂ Ф₁ cos (ψ + π/2) = - c₃ I ₂₂ Ф₁ sin ψ,                    (3.1)

где c₃ – постоянный коэффициент; ψ – угол между векторами потоков Ф₁ и Ф₂. Среднее значение силы при взаимодействии Ф₂ и I ₁₁:

             F₄ = c₄ I ₁₁ Ф₂ cos α ₂ = c₄ I ₁₁ Ф₂ cos (-ψ + π/2) = c₄ I ₁₁ Ф₂ sin ψ,                     (3.2)

где c₄ – постоянный коэффициент.

Согласно (3.1, 3.2) и учитывая направления потоков, токов и сил:

F = F₄ + (- F₃) = (c₃ I ₂₂ Ф₁ + c₄ I ₁₁ Ф₂) sin ψ.                                  (3.3)

При однородном строении диска и синусоидальном изменении потоков:        

 I ₁₁ = k₁ƒ Ф₁ и I ₂₂ = k₂ƒ Ф₂,

где ƒ – частота.

Тогда выражение (3.3) примет вид: F= kƒ Ф₁Ф₂ sin ψ.

Вращающий момент равен произведению силы на плечо h:

M= Fh = kh ƒ Ф₁Ф₂ sin ψ = с₅ ƒ Ф₁Ф₂ sin ψ,

где c₅ – постоянный коэффициент.

При слабом насыщении магнитопровода счётчика:

Ф₁ = k₃ I₁;  Ф₂ = k₄ I₂,

тогда                     M = k h k₃ k₄ ƒ I₁ I₂ sin ψ = с₆ I₁ I₂ ƒ sin ψ,                                    (3.4)

где k₃, k₄, c₆ – постоянные коэффициенты; I₁, I₂ – токи в параллельной и последовательной цепях счётчика, вызывающие появление потоков Ф₁ и Ф₂.

Согласно 3.4 вращающий момент диска счётчика пропорционален частоте тока измерительной цепи, что вызывает погрешность измерения.

На рисунке 3.6 дано графическое пояснение принципа работы счётчика

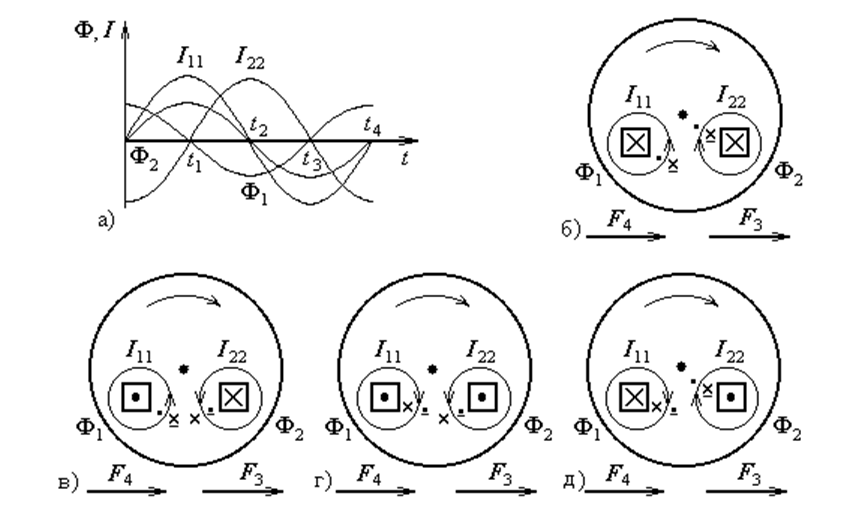Рис. 3.6 Графические пояснения принципа работы счётчика:

а – векторная диаграмма; б – интервал времени 0 – t₁; в – интервал

времени t₁ – t₂; г – интервал времени t₂ – t₃; д – интервал времени t₃ – t₄

индукционной системы. В качестве примера выбран режим, когда угол ψ между векторами потоков Ф₁ и Ф₂ равен  90° и вращающий момент M максимален (уравнение 3.4). Из рис. 3.6 следует, что поток Ф₁ притягивает ток I₂₂, а Ф₂ отталкивает I₁₁.

Для измерения индукционным счётчиком активной энергии, согласно выражению 3.4, необходимо получить sin ψ = cos φ, или ψ = π/2 – φ, где φ – угол между векторами тока I и напряжения U в измерительной цепи. С этой целью регулируется значение Ф_L за счёт изменения ширины воздушного зазора в магнитопроводе паралельной цепи счётчика. Это приводит к изменению угла вектора потока Ф_U, проходящего через диск счётчика (рис. 3.1) и вызывающего его вращение.

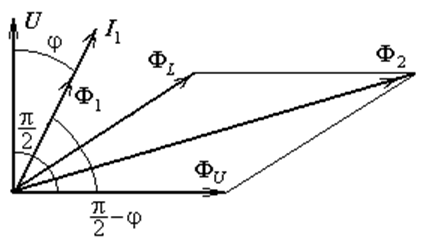На рис. 3.7 изображена векторная диаграмма регулировки угла потока Ф_U.

Для установления зависимости скорости вращения диска от потребляемой энергии используются постоянные магниты (рис. 3.1, позиция 6). Тормозной момент M_Т= kω, где ω – угловая скорость диска, k – постоянный коэффициент. При равенстве M_Т и M скорость вращения диска  постоянна   и   пропорциональна потребляемой энергии.

Рис. 3.7. Векторная диаграмма  энергии

                   регулировки углов

Погрешности индукционного счётчика

На рис. 3.8. изображена зависимость погрешности индукционного счётчика от тока нагрузки.

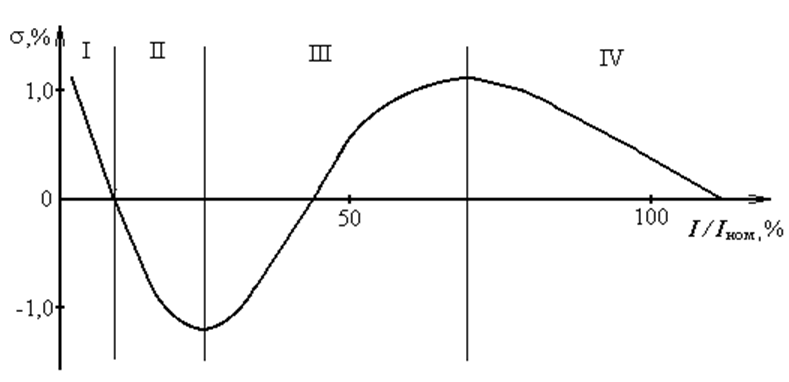Рис. 3.8 Зависимость погрешности от тока нагрузки

Причины возникновения погрешности на интервалах:

I – компенсационный момент превышает момент трения;

II – компенсационный момент меньше момента трения из-за возросшего тока и увеличения скорости вращения диска;

III – скорость вращения растёт так как Ф₁ растёт быстрее I₁ (нелинейный начальный участок кривой намагничивания);

IV – рост тормозного момента, вызванного потоком Ф₁.