Индуктивные сопротивления высокой и низкой стороны были найдены ранее (формула 15 и 16).
Активное сопротивление найдем воспользовавшись рекомендуемыми приближенными значениями [4, с.137]:
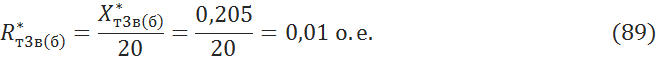
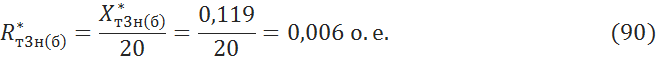
5.2 Преобразование схемы замещения
5.2.1 Эквивалентирование сопротивлений трансформаторов 
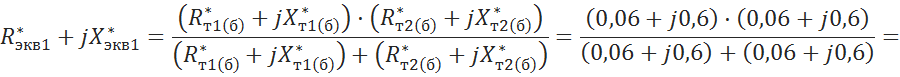
5.2.2 Преобразованная схема замещения
На основании выше проведенных расчетов составим схему замещения.
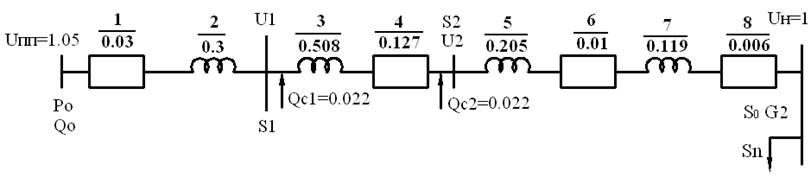
Рисунок 5.2 Схема замещения для расчета режима
5.3 Расчет линии
5.3.1 Вычисление потери мощности на трансформаторах
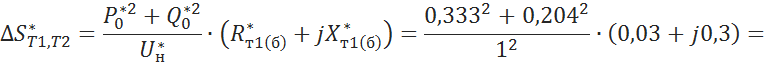
5.3.2 Вычисление мощность 
5.3.3 Вычисление потери мощности в линии:
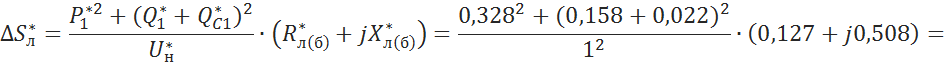
5.3.4 Вычисление мощность 
5.3.5
Вычисление потери мощности на трансформаторе 
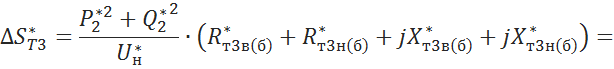
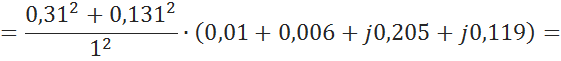
5.3.6 Вычислим
мощность 
:
5.3.7
Вычисление падения напряжения на трансформаторе
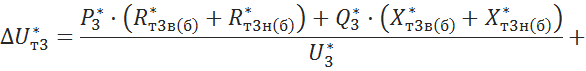
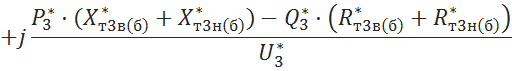
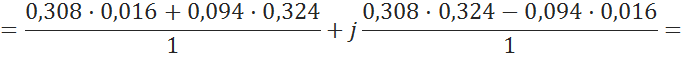
5.3.8
Вычисление напряжения за трансформаторами
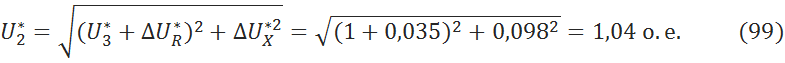
5.3.9 Вычисление падения напряжения на линии
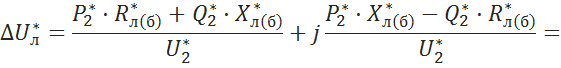
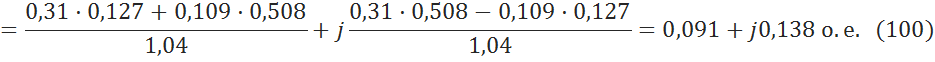
5.3.10 Вычисление напряжения за линией
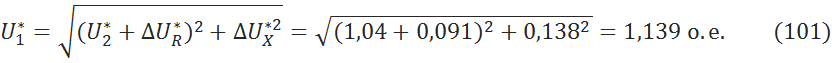
5.3.11
Вычисление падения напряжения на трансформаторах
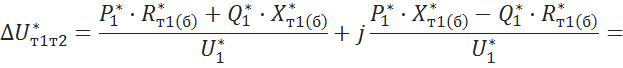
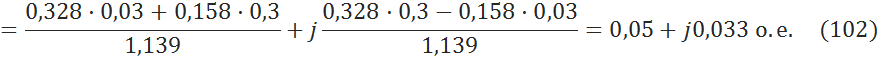
5.3.12 Вычисление напряжения пункта питания
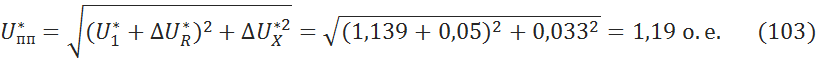
6 Расчет угловых характеристик
Турбина работает с мощностью 60% от номинального значения.
Пересчитаем при этом ЭДС генератора [2, c.22]:
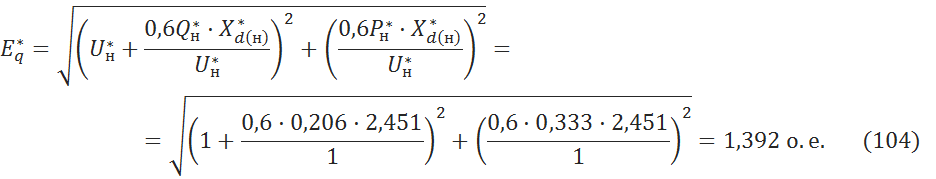
Найдем сопротивления, необходимые для расчета:
6.1 Без учета АРВ и явнополюсности
6.1.1 Построим зависимость активной мощности от угла δ [5, c.42]:
|
|
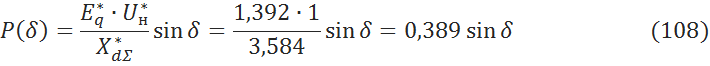
Рисунок 6.1 Зависимость активной мощности от δ без АРВ и явнополюсности
6.1.2 Предел мощности
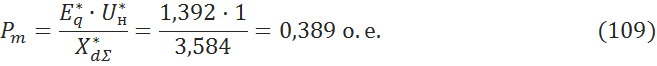
6.1.3 Коэффициент запаса [3, c.171]
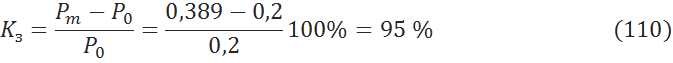
6.1.4 Построим зависимость реактивной мощности от угла δ:
|
|
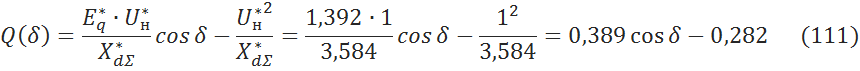
Рисунок 6.2 Зависимость реактивной мощности от δ без АРВ и явнополюсности
6.2 Без учета АРВ с явнополюсным генератором
6.2.1 Построим зависимость активной мощности от угла δ [3, c.179]:
|
|
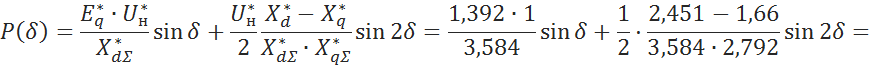
Рисунок 6.3 Зависимость активной мощности от δ без АРВ с явнополюсностью
6.2.2 Найдем угол, отвечающий максимуму электромагнитной мощности [5, c.48]
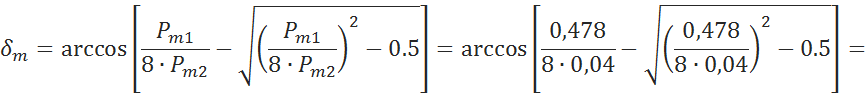
6.2.3 Предел мощности
6.2.4 Коэффициент запаса [3, c.171]
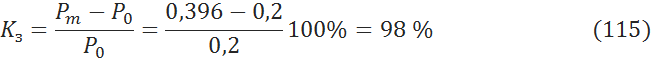
6.3 С учета АРВ пропорционального действия
6.3.1 Найдем переходную ЭДС [1, c.20]
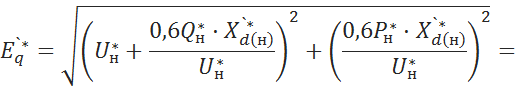
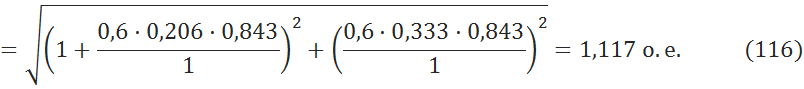
6.3.2 Построим зависимость активной мощности от угла δ [5, c.48]:
|
|
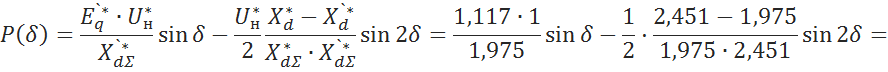
Рисунок 6.4 Зависимость активно мощности с учетом АРВ пропорционального действия
6.3.3 Найдем угол, отвечающий максимуму электромагнитной мощности [5, c.48]
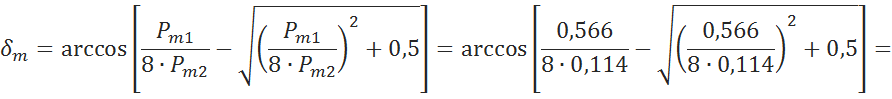
6.3.4 Предел мощности
6.3.5 Коэффициент запаса [3, c.171]
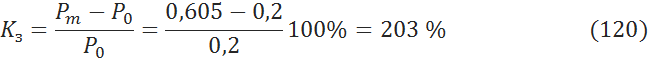
6.4 С учета АРВ сильного действия для явнополюсного генератора
6.4.1 Построим зависимость активной мощности от угла δ:
|
|
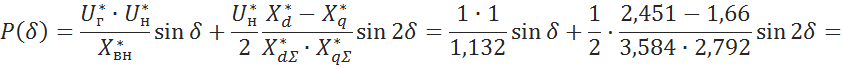
Рисунок 6.5 Зависимость активной мощности от δ при АРВ сильного действия
6.4.2 Найдем угол, отвечающий максимуму электромагнитной мощности [5, c.48]
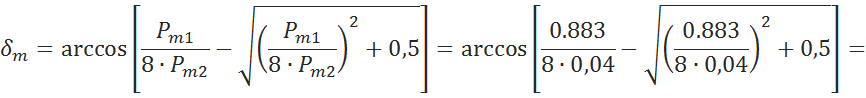
6.4.3 Предел мощности
6.4.4 Коэффициент запаса [3, c.171]
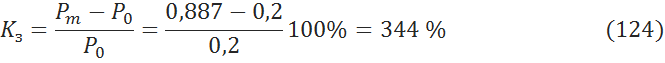
7 Расчет статической устойчивости системы
Рассчитаем статическую устойчивость системы «генератор – мощная система». Генераторы явнополюсные без АРВ и работают с номинальной мощностью. ЭДС генераторов была найдена в формуле 82:
Сопротивления необходимые для расчета были найдены в формулах 105 – 107.
7.1 Построим зависимость активной мощности от угла δ:
|
|
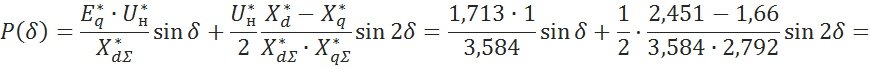
Рисунок 7.1 Зависимость активной мощности от угла δ
7.2 Найдем угол, отвечающий максимуму электромагнитной мощности [5, c.48]
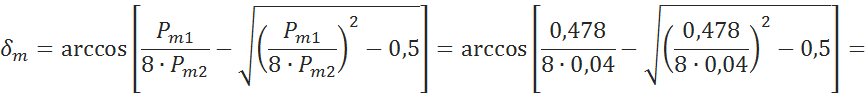
7.3 Предел мощности
7.4 Коэффициент запаса [3, c.171]
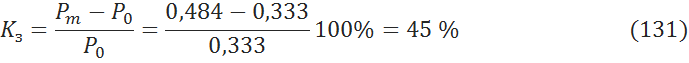
По нормам коэффициент запаса должен быть больше 20%. В данном случая коэффициент запаса равен 45%, что на много больше нормативного значения. Значит система статически устойчива.
8 Расчет динамической устойчивости
Трехфазное короткое замыкание происходит в точке, отделенной от шин высокого напряжения выключателем (рис. 1.1). При трехфазном коротком замыкание сопротивление схемы становится бесконечно большим, при этом характеристика мощности аварийного режима совпадает с осью абсцисс. Ротор генератора начинает свое относительное движение под воздействием избыточного момента, равного механическому моменту турбины. По нормативным документам время отключения короткого замыкания в сети 110 кВ равно 0,18 с. По расчетам требуется качественным (графическим) методом определить предельный угол или время включения сети, при которых ещё возможен ввод генератора в работу без дальнейшего нарушения его устойчивости (выпада из синхронизма).
Метод площадей заключается в том, чтобы площади торможения и ускорения были одинаковы, или первая площадь была больше второй. Площади характеризуют кинетическую энергию, которую ротор накапливает и отдает при ускорении или торможении. Если кинетическая энергия, накопленная ротором больше, которой необходимо для торможения, то генератор выпадет из синхронизма.
|
|
Рисунок 8.1 Характеристика системы
8.1
Найдем угол 
, когда
система работает в нормальном режиме:
Откуда
8.2 Определение угла, при котором произойдет отключение короткого замыкания
8.2.1 Найдем постоянную инерции [1, c.30]:
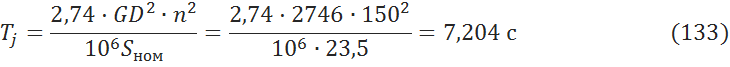
где 
-
маховой момент, 
; n – скорость вращения
генератора, об/мин; 
-
номинальная мощность генератора, МВА.
Расчет лучше провести в радианах.
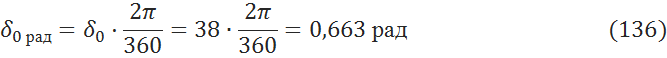
8.2.2 Расчет угла отключения короткого замыкания [3, с.226]:
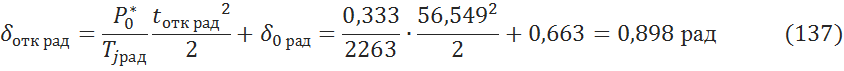
В градусах:
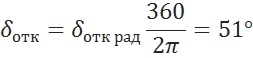
8.3 Определение критического угла
Определим угол, пройдя который, генератор выпадет из синхронизма.
В радианах:
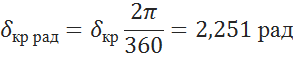
8.4 Определение предельного угла включения линии [3, c.226]
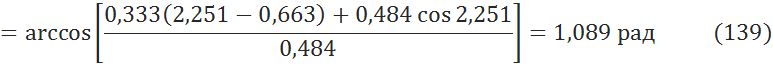
В градусах:
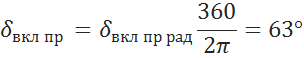
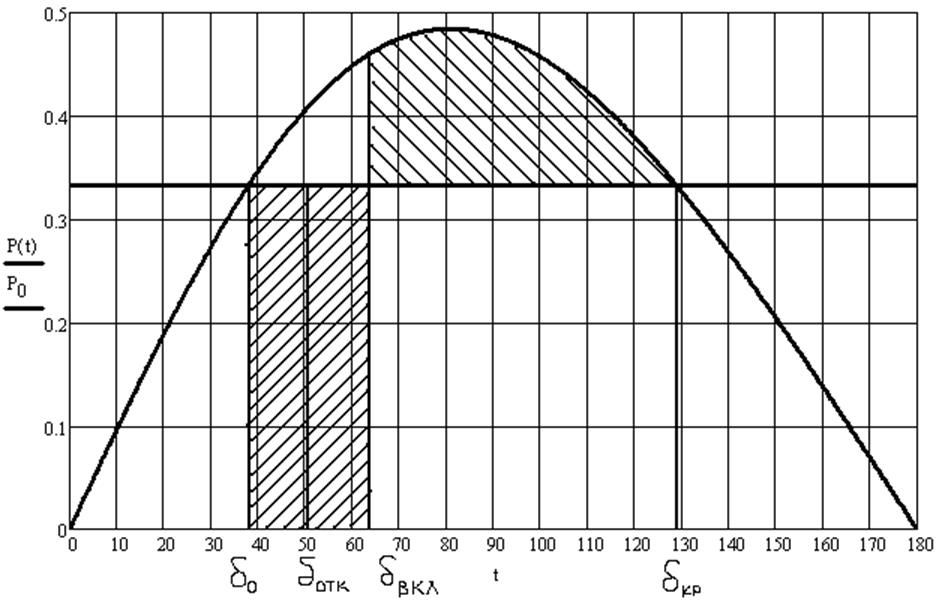
Рисунок 8.2 Определение угла включения по правилу площадей
8.5 Определение предельного времени включения линии [3, c.226]
Для практических целей недостаточно знать угол включения, необходимо располагать временем включения.
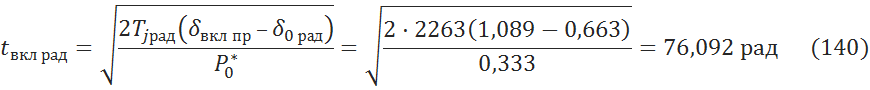
В секундах:
Список используемой литературы
1. Переходные процессы в электрических системах. Задания и методические указания на курсовую работу и контрольное задание для студентов факультета энергетики дневного и заочного отделения / Д.В. Армеев, А.П. Долгов, В.М. Чебан. – Новосибирск: Изд-во НГТУ, 2007. – 60 с.
2. Электромагнитные переходные процессы в электрических системах: сб. задач / Е.П. Гусев, А.П. Долгов, Л.И. Пушкарева, А.В. Коновалов, В.М. Чебан, Э.М. Чекмазов; под ред. В.М. Чебана. – Новосибирск: Изд-во НГТУ, 2007. – 123 с.
3. Переходные процессы в электрических системах: учеб. пособие / Ю.А. Куликов. – Изд. 2-е, испр. и доп. – Новосибирск: Изд-во НГТУ, 2006. – 284с.
4. Ульянов С.А. Электромагнитные переходные процессы в электрических системах. Учебник для электротехнических и энергетических вузов и факультетов. М., «Энергия», 1970.
5. Устойчивость электрических систем: учеб. пособие/ А.П. Долгов. – Новосибирск: Изд – во НГТУ, 2010. – 176 с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
