Мультиплексоры. Реализация логических функций на мультиплексорах, страница 2

№	Входы				Выходы
	Служебные	Информационные		Адресные
	EI	X1	X0	A0	F
1	0	–	–	–	0
2	1	0	0	0	0
3	1	0	1	0	0
4	1	1	0	1	X0
5	1	1	1	1	X0

На основании табл. 3.6 разработано устройство на MUX(2-1), рис. 3.5:

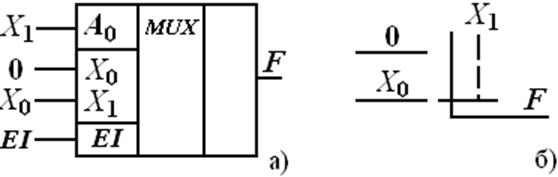
Рис. 3.5 Подключение мультиплексора: а – микросхема, б – механический аналог на переключателе для реализации логической функции

Схему также можно упростить, т.к. наборы 2, 3 (табл. 3.5) можно объединить, подав на А₀: A₁=0, при этом F =X₀ =0 (константа 0); на наборах 4, 5:  A₁=1, а значение функции F повторяет значения A₀, которое подается на X₁ (табл. 3.7, рис. 3.6).

Таблица истинности устройства                                           Таблица 3.7

№	Входы				Выходы
	Служебные	Информационные		Адресные
	EI	X1	X0	A1	F
1	0	–	–	–	0
2	1	–	0	0	0
3	1	1	–	1	A0

На основании табл. 3.6 разработано устройство на MUX(2-1), рис. 3.5:

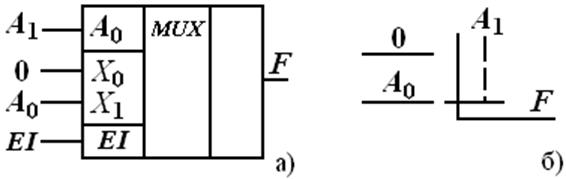
Рис. 3.6 Подключение мультиплексора: а – микросхема, б – механический аналог на переключателе для реализации логической функции

Реализация БФ с уменьшением количества информационных входов

Пример. Задана функция, составляется ее таблица истинности:

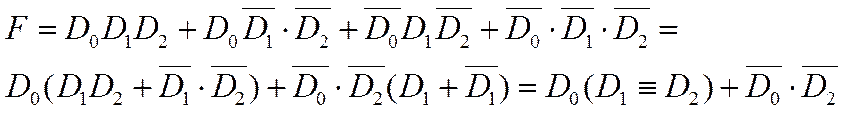
Таблица истинности                                                                                                    Таблица 3.8

№	D2	D1	D0	F
0	0	0	0	1
1	0	0	1	1
2	0	1	0	1
3	0	1	1	0
4	1	0	0	0
5	1	0	1	0
6	1	1	0	0
7	1	1	1	1

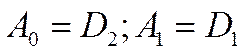
Пусть:

Составляем карту Карно и два горизонтально расположенных входных информационных сигналов D₁, D₂ используем для подачи на адресные входы A₀, A₁. Оставшийся информационный сигнал D₀ будем использовать для подачи на информационные входы MUX.

Из карты Карно следует, что при всех значениях D₀ для D₁, D₂ равных 0, 0 (подключен информационный вход D₀) на выходе 1. Аналогичные соображения для других комбинаций D₁, D₂.

Карта Карно                                                                                                                  Таблица 3.9

D1D2 D0	00	01	11	10
0	1	0	0	1
1	1	0	1	0
Информационные Входы	X0	X1	X3	X2

Из таблицы 3.9 следует, что значения D₂D₁: 00 – константа 1; 01 – константа 0;10 – инверсия D₀; 11 – D₀. Эти значения представлены в таблице 3.10.

Таблица истинности                                                                                                  Таблица 3.10

№	A1	A0	D	F
1	0	0	1	X0
2	0	1	0	X1
3	1	0	D0’	X2
4	1	1	D0	X3

D₀' – инверсное значение D₀

На рис. 3.7 представлена реализация БФ трех переменных с помощью MUX(4 – 1) согласно таблице 3.10. Если бы не минимизация, то потребовался бы MUX(8 – 1).

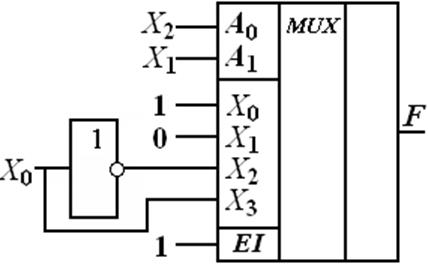
Рис. 3.7 Реализация БФ трех переменных с помощью MUX(4 – 1)

Увеличение разрядности мультиплексора

Используя два мультиплексора, например, MUX(2-1) количество входов можно увеличить в два раза, реализуя MUX(4-1), если подавать на входы EI старший разряд адресной переменной (A₁) со своими значениями, заданными в функции. Этот сигнал будет попеременно подключать в работу первый или второй мультиплексор (рис. 3.6, а; табл. 3.7).

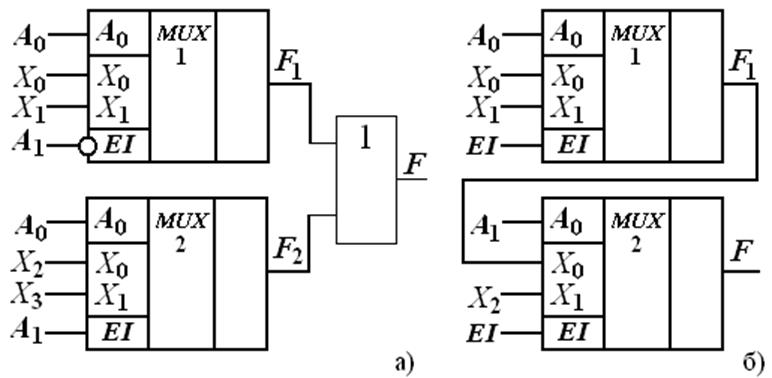
Рис. 3.7 Увеличение разрядности, а – реализация MUX(4-1) на двух MUX(2-1),

б –  реализация MUX(3-1) на двух MUX(2-1)

Таблица истинности  MUX(4-1)                                      Таблица 3.7

№	Входы							Выходы
	Служебные	Информационные				Адресные
		MUX 2		MUX 1
	EI	X3	X2	X1	X0	A1	A0	F
1	1	–	–	–	X0	0	0	X0
2	1	–	–	X1	–	0	1	X1
3	1	–	X2	–	–	1	0	X2
4	1	X3	–	–	–	1	1	X3

Аналитическое выражение работы MUX(4-1), согласно таблице 3.7 и схеме рис. 3.7, а:

 

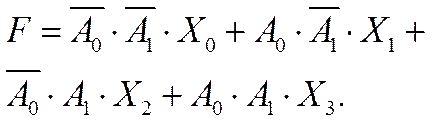Также увеличение разрядности мультиплексоров можно осуществить за счет их пирамидального включения (рис.3.8).

Из таблицы 3.3 следует, что четным номерам информационных входов X соответствует значение адреса A₀ = 0 и эти входы подключены к MUX 1. Для нечетных номеров информационных входов X адрес A₀ = 1 и эти входы подключены к MUX 2. Младший адресный разряд A₀ используется для управления мультиплексором MUX 3.

 В результате из двух мультиплексоров MUX(4-1) и одного MUX(2-1) получился MUX(8-1). Недостаток схемы – снижение быстродействия за счет последовательного включения микросхем. В результате время переключения составит сумму интервалов переключений MUX 1 (MUX 2) и MUX 3. 

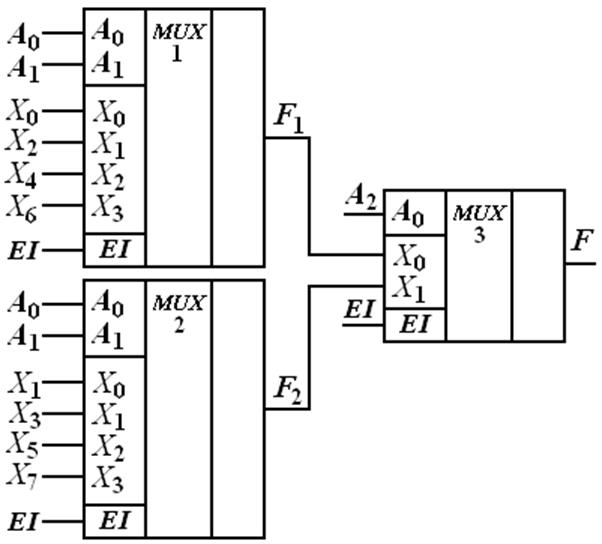
Рис. 3.8 Пирамидальное включение мультиплексоров для увеличения разрядности

Аналитическое выражение, соответствующее схеме MUX(8-1), рис. 3.8, если EI = 1:

 

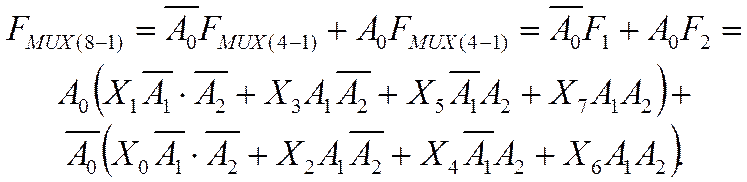Данное выражение можно получить из таблицы истинности 3.3 согласно стандартной процедуре.

Достоинство пирамидальной схемы – использование однотипных элементов.

Мультиплексоры также используются для одновременного подключения n- разрядных слов в соответствии с адресом на n- разрядный выход в параллельном коде.

Одновременно к n выходам подключаются n входов. При изменении значения адреса к n выходам одновременно подключаются другие n входов. Мультиплексор обозначается MUX(k – n вn), гдеk - количество слов.

Например, MUX(4 – 8 в 8) – четыре восьмибитовых слов выборочно передаются на восьмибитовый выход согласно двухразрядному адресному двоичному коду. Применяется в микропроцессорной технике.

Мультиплексоры используются в составе больших интегральных микросхем, например, микропроцессоров, где к одному выходу подключается несколько внутренних источников сигналов. Это позволяет уменьшить размеры микросхем за счет снижения числа выходов, и, следовательно, повысить их быстродействие. В микропроцессорах с одних выходов могут передаваться сигналы линий шины данных и шины адреса, передаваемые последовательно во времени, например, с помощью MUX(4 – 8 в 8).

Примеры использования мультиплексоров:

- передача данных от нескольких источников сигналов по общему каналу с разделением во времени;

- преобразование параллельного кода в последовательный код (модем);

- постоянные запоминающие устройства;

- в качестве дешифраторов;

- регистры сдвига (совместно с приоритетным шифратором);

- преобразование целых чисел из формата с фиксированной запятой в формат с плавающей запятой и обратное преобразование;

- для передачи четырех восьмибитовых слов в параллельном коде на восьмибитовый выход. Применяется в микропроцессорной технике.