Мультиплексоры. Моделирование мультиплексоров

Лабораторная работа 2.5

Мультиплексоры

Основные теоретические положения

Мультиплексор – комбинационное цифровое устройство для управляемой передачи данных от нескольких источников информации X  в один выход F согласно коду адреса A.

Мультиплексор имеет n адресных шин, m = 2ⁿ – входов и один информационный выход F. Обозначение MUX(m-1).

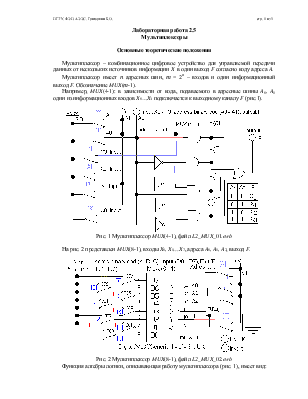
Например, MUX(4-1): в зависимости от кода, подаваемого в адресные шины A₀, A₁ один из информационных входов X₀…X₃ подключается к выходному каналу F (рис.1).

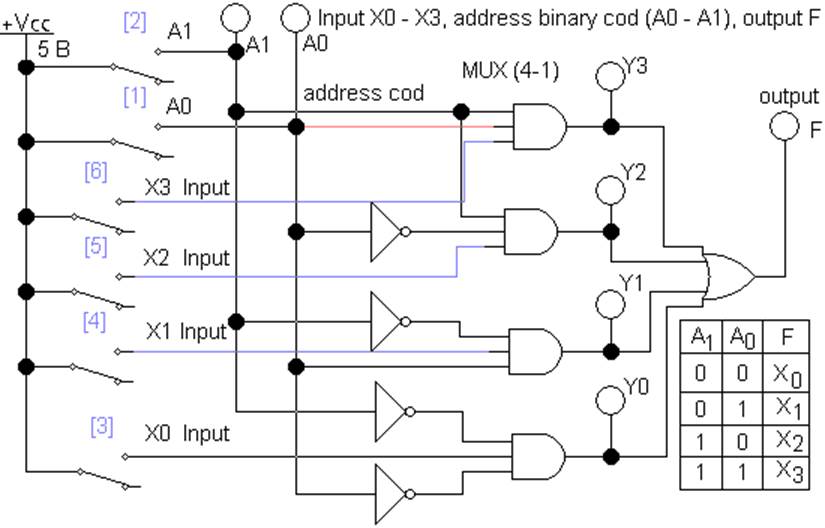
Рис. 1 Мультиплексор MUX(4-1), файл L2_MUX_01.ewb

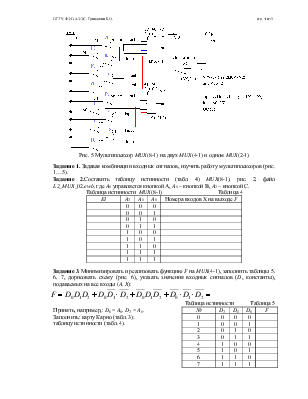
На рис. 2 представлен MUX(8-1), входы X₀, X₁…X₇, адреса A₀, A₁, A₂, выход F.

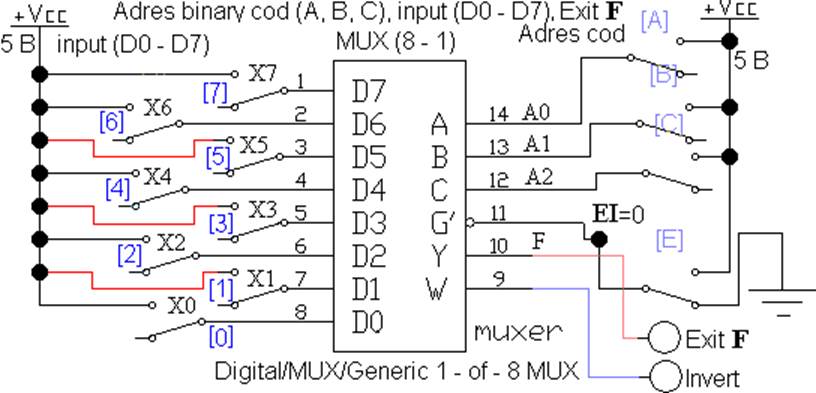
Рис. 2 Мультиплексор MUX(8-1), файл L2_MUX_02.ewb

Функция алгебры логики, описывающая работу мультиплексора (рис. 1), имеет вид:

 

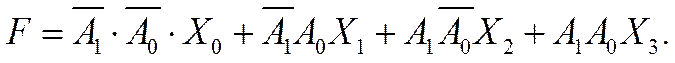Файлы для моделирования мультиплексоров расположены в папке Lab_2_5\Модели.

Мультиплексоры имеют разрешающий вход EI, если на него подается логическая единица, то происходит передача информации. На рисунке 2 этот вход инверсный.

На мультиплексорах можно реализовать любую логическую функцию. Например, необходимо получить логический элемент 3И (рис. 3). Для этого составляется  таблица истинности (табл. 1).

Таблица истинности элемента «И»   Таблица 1

№ входа X	A2	A1	A0	F
X0	0	0	0	0
X1	0	0	1	0
X2	0	1	0	0
X3	0	1	1	0
X4	1	0	0	0
X5	1	0	1	0
X6	1	1	0	0
X7	1	1	1	1

 

В соответствии с адресом, выход F подключается к соответствующему входу X. Если на эти входы подать логические сигналы согласно столбцу F, то получится требуемый элемент (рис. 3).

Используя табл. 1, согласно стандартным процедурам, можно записать аналитическое выражение работы мультиплексора:

 

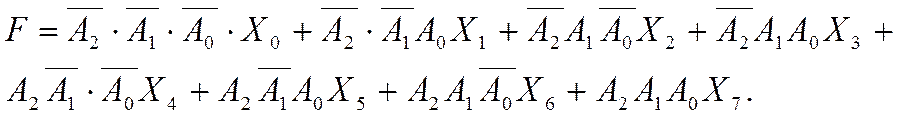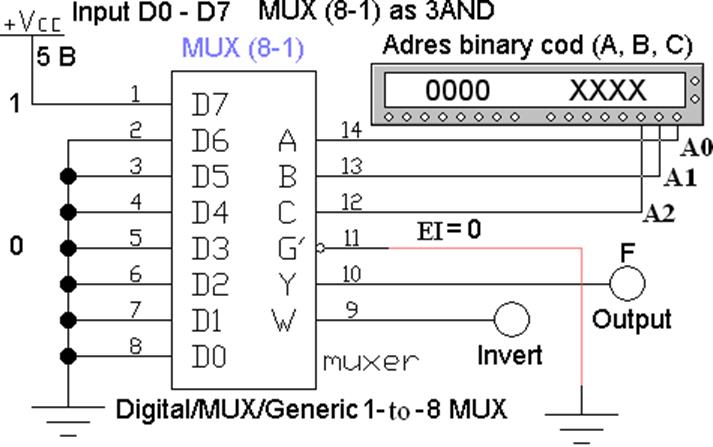
Рис. 3 Логический элемент 3И на мультиплексоре MUX(8-1), файл L2_MUX_03.ewb

Пример. Реализовать функцию  F на MUX(4-1):

 

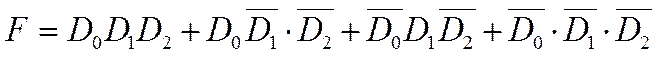Последовательность операций:

Адресных входов меньше, чем переменных X. Поскольку D₀ и D₁ входят во все слагаемые группы сомножителей в прямом и инверсном виде, примем: D₀ = A₀; D₁ = A₁.

Составим карту Карно (табл. 2), используя аналитическое выражение для определения значений функции F в клетках данной таблицы. Наборам адресов A₀; A₁ соответствуют входы мультиплексора X, которые подключаются к выходу F (таблицы 2, 3).

Из таблицы 2 следует, что на первых трех наборах адресов, функция F равна инверсному значению D₂. Для четвертого набора F = D₂. Схема устройства представлена на рис. 4. Выход микросхемы 74352 инверсный, поэтому к нему подключен инвертор.

Карта Карно                                          Таблица  2             Таблица истинности        Таблица 3

D2D0 D1	00	01	11	10		№	D	A1	A0	F
0	1	1	0	1		1	D2'	0	0	D0
1	0	0	1	0		2	D2'	0	1	D1
Информационные Входы	X0	X1	X3	X2		3	D2'	1	0	D2
						4	D2	1	1	D3

            X₂' – инверсное значение X₂

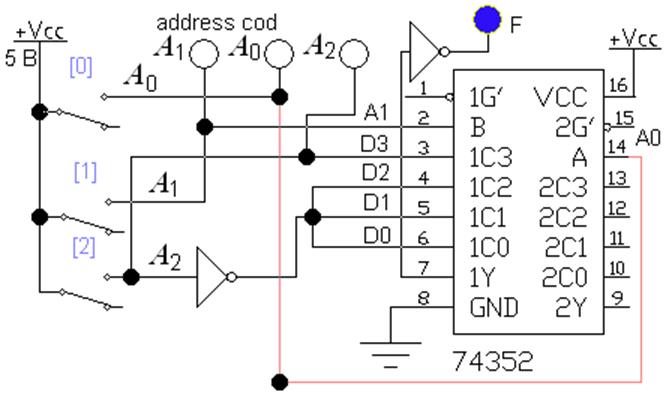
Рис. 4 Реализация логической функции на мультиплексоре MUX(4-1), файл L2_MUX_04.ewb

Для увеличения разрядности мультиплексора используются разрешающие входы EI.

На рис. 5 представлен MUX(8-1)на двух MUX(4-1) и одном MUX(2-1).

Мультиплексоры расположены в модулях 1, 2, 3, которые раскрываются двойным щелчком мыши.

Переключение между мультиплексорами (4-1) осуществляется с помощью старшего адресного разряда A₂, который управляет работой MUX(2-1): первые четыре набора для X₀…X₃ считываются с MUX1, когда A₂=0, наборы X₄…X₇ с MUX2, при A₂=1.

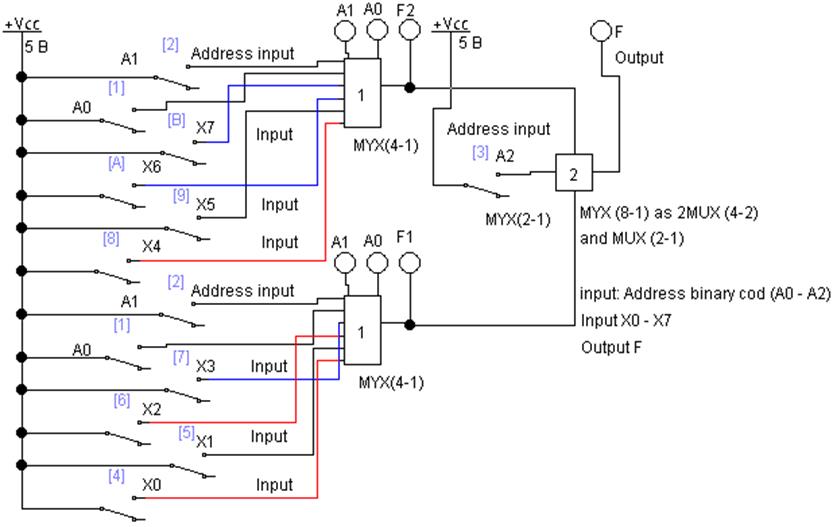
Рис. 5 Мультиплексор MUX(8-1) на двух MUX(4-1) и одном MUX(2-1)

Задание 1. Задавая комбинации входных сигналов, изучить работу мультиплексоров (рис. 1…5).

Задание 2.Составить таблицу истинности (табл. 4) MUX(8-1), рис. 2, файл L2_MUX_02.ewb, где A₀ управляется кнопкой А, A₁ – кнопкой В, A₂ – кнопкой С.

Таблица истинности  MUX(8-1)                                       Таблица 4

EI	A2	A1	A0	Номера входов X на выходе F
	0	0	0
	0	0	1
	0	1	0
	0	1	1
	1	0	0
	1	0	1
	1	1	0
	1	1	1
	1	1	1

Задание 3. Минимизировать и реализовать функцию F на MUX(4-1), заполнить таблицы 5, 6, 7, дорисовать схему (рис. 6), указать значения входных сигналов (D, константы), подаваемых на все входы (A, X):

 

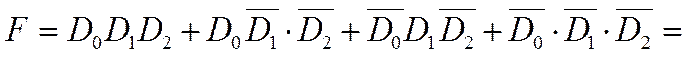
                                                                                            Таблица истинности           Таблица 5

Принять, например,: D0 = A0, D2 = A1. Заполнить: карту Карно (табл. 3); таблицу истинности (табл. 4).	№	D2	D1	D0	F
	0	0	0	0
	1	0	0	1
	2	0	1	0
	3	0	1	1
	4	1	0	0
	5	1	0	1
	6	1	1	0
	7	1	1	1

Карта Карно                                        Таблица  3               Таблица истинности        Таблица 4

D2D0 D1	00	01	11	10		№	D	A1	A0	F
0						1		0	0	X0
1						2		0	1	X1
Информационные Входы	X0	X1	X3	X2		3		1	0	X2
						4		1	1	X3

Выводы:

С помощью мультиплексора можно реализовать любую логическую функцию, предварительно преобразовав ее в совершенную дизъюнктивную нормальную форму (соответствует таблице 2).  

Количество адресных входов (A) может быть меньше числа переменных (D), если использовать рассмотренные преобразования (задание 3).

Рис. 6 Реализация логической функции            На рис. 1 представлена реализация БФ трех

                                                                          переменных с помощью MUX(4 – 1) согласно таблице 4. Если бы не преобразования, то потребовался бы MUX(8 – 1).

Задание 4. Перечислить, где и для каких целей применяются мультиплексоры.