Линейная модель режима электрической сети

5. Линейная модель режима электрической сети

Краткие теоретические сведения

Электрическая сеть состоит из множества соединенных между собой элементов. Обычно все элементы электрической сети моделируются П-образными схемами замещения. Для простоты и обозримости схем электрических сетей их изображают в виде графов, в которых вершинами являются узловые точки сети, а ребрами – продольные элементы П-образных схем замещения. Поперечные ветви П-образных схем замещения являются ребрами графа, соединенные с вершиной N – нейтральной точкой трехфазной системы и для простоты не изображаются на графе.

На рис. 5.1,а показан пример принципиальной схемы сети, а ее схема замещения на рис. 5.1,б. После эквивалентных преобразований поперечных ветвей получают эквивалентную схему замещения с меньшим числом поперечных элементов, рис. 5.2,а (на рисунке  с помощью пунктирных линий показаны поперечные элементы, которые для каждого узла преобразуются в один эквивалентный элемент). Наиболее просто выглядит граф сети, построенный на продольных элементах схем замещения элементов сети, рис. 5.2,б.

Моделирование режимов электрических сетей

Для решения многих задач управления и проектирования в ЭЭС необходимы данные о режиме электрической сети. Установившиеся режим характеризуется режимными параметрами, некоторые из которых могут быть измерены, другие – рассчитаны. В проектных задачах измерения невозможны, поэтому их заменяют значениями, полученными в результате прогнозов.

Расчет установившегося режима может выполняться при разных условиях, которые определяются набором данных для расчета. В традиционной постановке известными считают узловые мощности (нагрузки и генерации), а так же  напряжение одного из узлов, который называется базисным узлом. Перечисленные данные относятся к независимым параметрам в расчете режима; на их основе вычисляются другие параметры, которые называются зависимыми. К ним относятся узловые напряжения, токи, потоки мощности и потери в элементах электрической сети. Один из узлов схемы должен быть балансирующим, т.е. выполнять функции осуществления баланса мощности во всей сети. Его мощность также подлежит вычислению. Обычно базисный и балансирующий узлы совмещают. Будем называть такой узел базисным балансирующим узлом.

Параметры элементов электрической сети получаются на основе справочных данных по оборудованию. Они необходимы для вычисления параметров моделей ЛЭП, трансформаторов и других устройств.

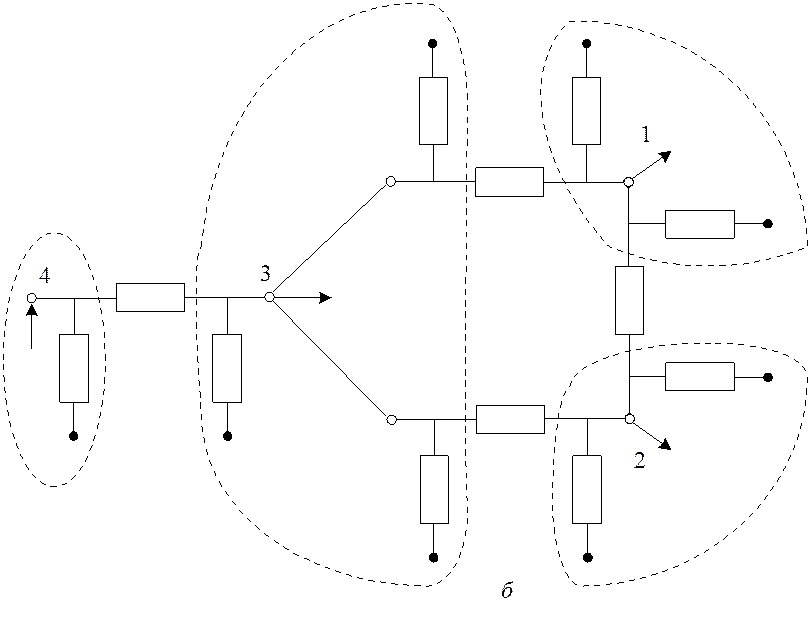
Рис. 5.1. Пример электрической сети (а) и ее схема замещения (б)

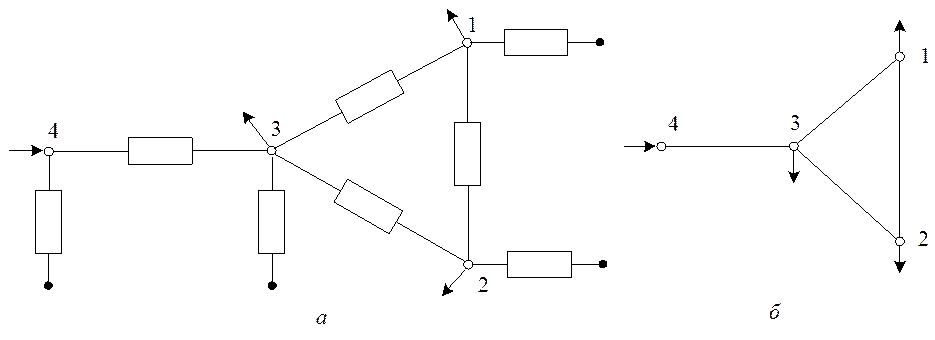
Рис. 5.2. Эквивалентная схема замещения сети (а) примера и ее граф (б)

Моделирование режима линейной электрической сети

Уравнения установившегося режима в линейной форме имеют вид

,                                                                                                   (5.1)

где     Y – матрица узловых проводимостей;

   Y₀ – вектор проводимостей ветвей, связанных с базисным балансирующим узлом;

   U – вектор узловых напряжений;

   J – вектор задающих токов узлов;

   U₀ – напряжение базисного узла.

Здесь токи для удобства записи увеличены в  раз.

Задающие токи, как правило, не известны, но могут быть приближенно вычислены через мощности нагрузок и генерации и номинальные напряжения узлов. 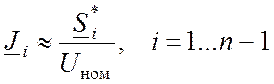(n – общее число узлов в схеме сети).

Решение системы уравнений (5.1) записывается в виде:

.                                                                                                   (5.2)

В некоторых случаях можно представить нагрузки в виде проводимостей, приближенно вычисленных через номинальные напряжения, и перейти к другой линейной модели:

                                                                                                   (5.3)

или

.                                                                                                   (5.4)

Решение системы уравнений (5.4) записывается в виде:

.                                                                                                   (5.5)

Методика выполнения работы

Для решения уравнений (5.1) требуется получить матрицы Y и Y₀, а для уравнений (5.4) еще матрицу Y_н.

Использование задающих токов и проводимостей нагрузок, рассчитанных по номинальным напряжениям, вносит погрешность в линейные математические модели режима, однако в некоторых случаях подобное упрощение вполне допустимо. В то же время линейная модель значительно упрощает расчет режима сети, т.к. процесс вычислений может быть не итерационным и тогда не существует проблемы сходимости вычислительного процесса.

Матрица узловых проводимостей может быть получена посредством матрицы M – матрицы соединений:

.                                                                                                   (5.6)

где Z^-1_в – квадратная матрица сопротивлений продольных ветвей графа сети.

 Матрица Y₀ составляется для ветвей, соединенных с базисным балансирующим узлом и имеет размерность по числу узлов без базисного узла. Для узлов, которые не имеют связи с базисным узлом, элементы матрицы равны нулю.

Таким образом, формирование линейной модели режима электрической сети сводится к получению матриц: Y, Y₀, (Y_н), J .

После решения линейных уравнений установившегося режима требуется вычислить остальные параметры режима. К ним относятся:

I – вектор токов в продольных ветвях П-образных схем замещения элементов сети;

S_b – вектор потоков мощностей в начале каждой ветви;

S_e – вектор потоков мощностей в конце каждой ветви;

DS = DP + jDQ – вектор потерь активной и реактивной мощности в каждой ветви.

Зарядная мощность и потери мощности в ЛЭП вычисляются в виде их суммы, поэтому по DQ можно выяснить какая из этих двух мощностей преобладает в линии.

Баланс мощности в сети показывает, насколько точно сбалансирован режим: сумма мощностей узлов и потерь в ветвях должна быть равна мощности балансирующего узла. Небаланс мощности можно считать погрешностью расчета.