Коммерческие особенности управления режимами энергосистем: Конспект лекций в примерах и задачах, страница 5

Субъектами рыночных отношений на балансирующем рынке могут выступать маневренные электростанции, имеющие свободные генерирующие мощности, и потребители с регулируемой нагрузкой. При этом участие в этом рынке обязательно для всех генерирующих мощностей, отобранных на рынках резервов.

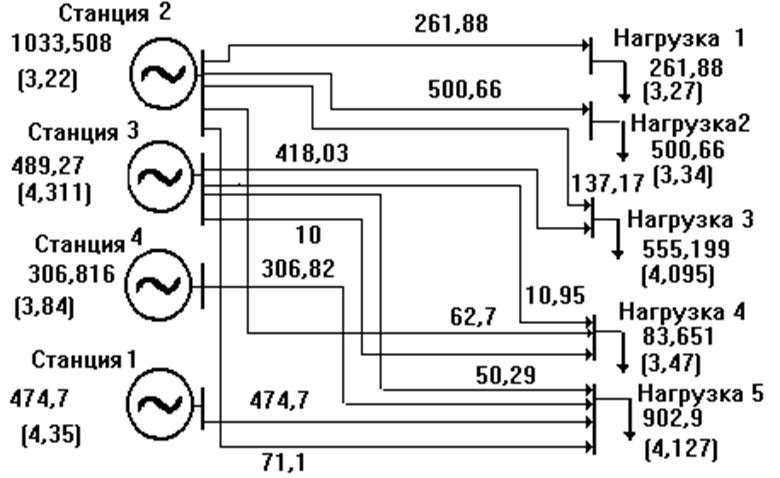
Рассмотренная задача сейчас решается как транспортная задача линейного программирования (табл. 1.5). Пример расчета дан на рис.1, на котором показаны потоки стоимостей. Указаны полные и удельные издержки каждой станции и каждой нагрузки. Цифры условные. Удельные издержки в узлах нагрузки определяют узловые цены. В полученном балансе не догружены  станция 3,4 и 5 (табл. 1.6). При изменении исходного режима баланс корректируется с учетом удельных стоимостных показателей станций. Имеются ограничения по ЛЭП и  станция 3 не может выдать мощность более 80%.

Таблица 1.5

Линейная модель составления баланса продаж и покупок на электроэнергетическом рынке

Таблица 1.6.

Корректировка баланса мощности при изменении нагрузки

	Номера станций
	1	2	3	4
Нагрузка, %	100	90	70	50
Свободная мощность, % от общей нагрузки системы в исходном режиме	0	10	30.	50
Небаланс мощности при росте нагрузки: в исходном режиме – 0, при увеличении нагрузки к исходному режиму: а. на 10%, б. на 20 %, в. при снижении  нагрузки на  20%	0		10	0
Изменение затрат по отношению к исходному режиму: а.	0		30,84	0
б.
в.

Рис. 1.3. Стоимостные оценки мощности по транспортной модели

Задание для расчета

1.  Выполнить расчеты для вариантов б и в и показать их в табл. 1.6

2.  Оценить в руб. влияние ограничений по ЛЭП при корректировке баланса.

3.  Рассчитать средние удельные издержки по системе.

Аналитическое задание

Обосновать применение линейной модели расчетов. В чем ее достоинство и недостатки.

1.7. Оптимизация режима ЭЭС – задача 4.

Задача оптимизации режимов  ЭЭС является классической [ю], поэтому она не излагается подробно. Однако надо помнить, что может быть множество допустимых режимов и для минимизации издержек необходимо найти в нем оптимальное решение. От издержек зависят цены, а следовательно и все коммерческие результаты. В данной задаче необходимо дать ее достаточно правильную постановку и указать состав исходной информации и принципы решения.

В табл.1.7 приведена математическая модель задачи оптимизации режимов ЭЭС. Необходимо для примера, данного на рис. 1.  дать  расшифровку математической модели:

·  записать составляющие уравнения цели,

·  пояснить содержание и координаты уравнений связи,

·  пояснить, почему появляются ограничения,

·  дать пример метода оптимизации.

·  Оценить эффективность оптимизации на основании сравнения результатов рис.1.    и 1.   , для которых использовались одинаковые условия расчетов.

·  Пояснить за счет каких факторов возросли издержки.

Таблица 1.7.

Математическая модель задачи оптимизации режимов ЭЭС для примера рис.1.

Модель оптимизации	Нелинейная модель оптимизации в общем виде	Пояснения на основании примера
Уравнение цели
Уравнения связи
Уравнения ограничений
Метод оптимизации	Методы нелинейного программирования

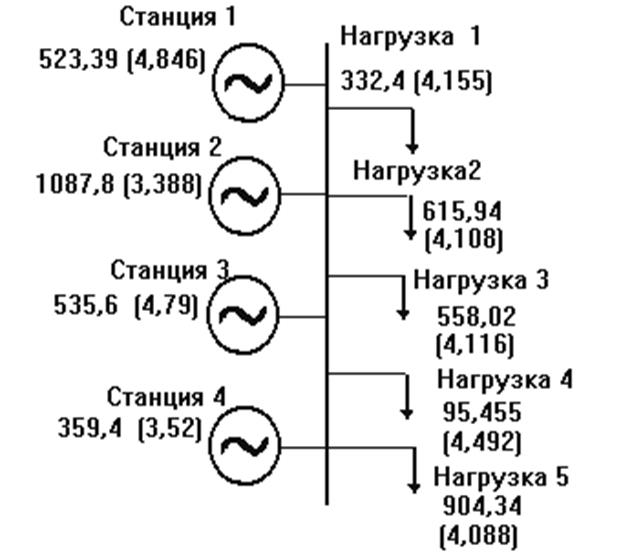
Рис.1.4. Стоимостные оценки мощности ЭЭС при учете издержек сети в характеристиках станций и оптимизации по методу неопределенных множителей Лагранжа

Раздел 2. Адресные оценки потоков и потерь мощности.

2.1. Общие положения

Поскольку понятие адресности не является общепринятым в энергетической литературе, то дадим пояснения. В этом понятии имеются четыре признака: отправитель, получатель, траектория их связи, идентификация отправления. Ряд задач в энергетике требуют выделения каждой индивидуальной траектории от поставщика энергии к потребителю. Возникает задача разделения общего потока электроэнергии на отдельные части. Термин «адресность» в зарубежной литературе используется как термин «трассировка» потока мощности.

Задачи адресного распределения могут рассматриваться  в технических и коммерческих целях. Имеется ряд общеизвестных адресных задач, которые преследуют технические цели: расчет и анализ потокораспределения в электрической сети, выявление очагов потерь, выявление ограничений по транспорту энергии и многие другие. В коммерческих задачах цель другая. Это определение стоимости потоков и потерь мощности и энергии при определении отношений купли – продажи между генерирующими единицами и потребителями – покупателями.

Рассмотрим некоторые задачи, в которых в той или иной форме учитывается адресность поставок электроэнергии потребителям.

1.  Расчет баланса покупки и продажи мощности и энергии на оптовом рынке с учетом электрической схемы системы и технических ограничений. Эта задача решается сейчас как транспортная задача линейного программирования, в которой учитывается только те ЛЭП электрической сети, по которым идет мощность, учитываемая в торговых соглашениях.

2.  Развитием первой задачи является расчет узловых цен в системообразующей сети оптового рынка. Это адресная задача. Узловые цены рассчитываются по регионам, зонам, крупным подстанциям.

3.  Оптимальное распределение активной или полной мощности в электроэнергетической системе и адресной оценкой стоимости потоков и потерь мощности в ее элементах (узлах и ветвях). Это задача нелинейного программирования, в которой используются определенные оптимизационные методы. Рассчитывается режим системы и ее параметры по активной  реактивной мощности, по напряжениям, рассчитываются потери мощности. Электрическая сеть представляется более широко, с учетом транспортной и распределительной ее частей. Это типовая задача региональных энергосистем и их потребительского рынка. Главной целью этих задач является определение мощности и энергии станций, в соответствии с требованиями потребителей. Поскольку электрическая энергия не складируется, то управление балансами ведется по схеме: прогноз – план - коррекция плана, т.е эта задача постоянно решается.