Исследование электрических свойств металлических проводниковых материалов, используемых в производстве электронных аппаратов, страница 3

,                                                (6.1)

где R - сопротивление проводника.

Для   измерения   удельного   электрического   сопротивления   на практике пользуются внесистемной единицей Ом*мм / м.

Наблюдаемый эффект способности металлов создавать сопротивление прохождению электрического тока зависит от их физической природы, а величина удельного сопротивления металлического проводника может быть определена по следующей формуле:

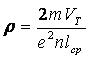                                                         ,                                      (6.2)      

где m - масса электрона; V - средняя скорость теплового движения электрона внутри металлического проводника;  - средняя длина свободного пробега электрона.

Рассеяние, приводящие к появлению сопротивления, возникает в тех случаях, когда в решетке имеются различного вида нарушения ее правильного строения, т.е. дефекты структуры. Дефекты структуры могут быть статическими, динамическими, атомными (точечными), протяжными. Однако и в чистых металлах с совершенной структурой присутствует эффект сопротивления свободному движению электронов. И причиной такого эффекта являются тепловые колебания атомов в узлах кристаллической решетки. Отсюда совершенно очевидно, что с ростом температуры увеличивается амплитуда колебаний атомов и связанные с ними флуктуации периодического поля решетки. А это, в свою очередь, усиливает рассеяние электронов и вызывает возрастание удельного сопротивления.

Электрическое сопротивление материала, обусловленное тепловым эффектом, обозначит через .

Для характеристики зависимости относительного изменения удельного сопротивления материала от температуры ввели понятие температурного коэффициента удельного сопротивления .

В диапазоне температур, где зависимость удельного сопротивления р от температуры Т близка к линейной, допустима линейно-кусочная аппроксимация этой зависимости, и величина удельного сопротивления в конце диапазона температуры Т может быть подсчитана по формуле:

                                                   ,                                         (6.3)

где  - удельное сопротивление в начале диапазона температур.
       Величину называют средним температурным коэффициентом  удельного сопротивления в данном диапазоне температуры:

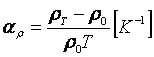                                      .                                           (6.4)

Дифференциальноевыражение для имеет вид:

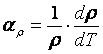                                                   .                                      (6.5)

Положительный знак соответствует случаю, когда удельное сопротивление в окрестности данной точки возрастает при повышении температуры. Величина также является функцией температуры. В области линейной зависимости от Т справедливо выражение:

                                             ,                                 (6.6)

где и - удельное сопротивление и температурный коэффициент удельного сопротивления, отнесенные к началу температурного диапазона, т.е. температуре То;  - удельное сопротивление при температуре Т.