Исследование логических элементов, реализующих элементарные функции алгебры логики, страница 2

Продолжение таблицы 10

0	1	0	0
0	1	0	1
0	1	1	0
0	1	1	1
1	0	0	0
1	0	0	1
1	0	1	0
1	0	1	1
1	1	0	0
1	1	0	1
1	1	1	0
1	1	1	1

Изучить работу моделей файла Lab1_18E.ewb, где приведены варианты реализации логического выражения:

Задание 4:

Найдите аналитическое выражение функции, которая реализуется схемой, приведенной на рисунке 1.1. Минимизируйте это выражение с помощью законов алгебры логики и согласно полученному результату соберите схему. Подключите входы A, B, C, D к источнику логических сигналов на выключателях, а выход Y – к логическому пробнику. Включите схему и проверьте правильность аналитического выражения. Подсказка: для реализации схемы используются логические операции эквивалентности и умножения.

Рис. 1.1 Схема логического устройства

Ответ.

Функция и подробная процедура ее минимизации (согласно схеме рис. 1.1):

Y=

Рис.1.2 Схема логического устройства после минимизации

(представляется в виде рисунка согласно российским стандартам)

Задание 5:

При монтаже схемы, приведенной на рисунке 1.3, а), была допущена ошибка: вместо элемента исключающее ИЛИ был использован элемент ИЛИ, рисунок 1.3, б). Найдите комбинации входных сигналов, которые позволяют выявить ошибку монтажника. Ответ указать в таблице 11.

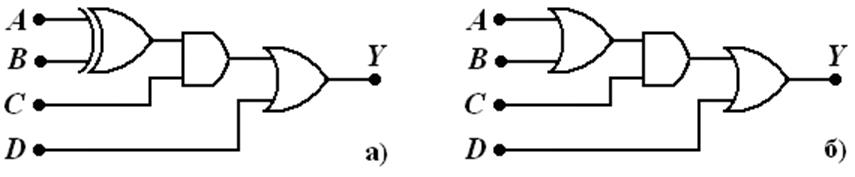
Рис. 1.3 Разработанная схема устройства, (а), собранная схема с ошибкой монтажа, (б)

Ответ.

Фрагмент таблицы истинности                                                                                  Таблица 11                                                           

№ набора	A	B	C	D	Y, схема а	Y, схема б

Задание 6:

Разработайте схему, формирующую на выходе сигнал Y из входных сигналов С, В, А как показано на рисунке 1.4. Соберите схему, которая должна содержать не более двух логических элементов. При проверке ее работы для формирования входных сигналов используйте источники логических сигналов на выключателях или генератор слов.

Рис. 1.4 Временная диаграмма работы логического устройства

Ответ.

Функция и подробная процедура ее минимизации (согласно временной диаграмме рис. 1.4):

Y =

Рис.1.5 Схема логического устройства после минимизации

(представляется в виде рисунка согласно российским стандартам)

Задание 7:

Проведите анализ работы логического устройства, собранного на микросхеме 7400, показанного на рисунке 1.6. Определите, какую логическую операцию (только одну) выполняет данное устройство. Для обоснования ответа представьте необходимые аналитические преобразования, используя законы алгебры логики. Соберите схему, подключите необходимые приборы и проведите экспериментальное исследование работы схемы.

Рис. 1.6 Схема логического устройства

Ответ.

Функция и подробная процедура ее минимизации (согласно схеме рис. 1.6):

Y =

Рис. 1.7 Схема логического устройства после минимизации

(представляется в виде рисунка согласно российским стандартам)

Задание 8. Изучить работу моделей файлов Lab1_19E.ewb, Lab1_20E.ewb, Lab1_21E.ewb.

Выводы:

1. Логические функции можно задавать словесно, таблично, графически, аналитически, в виде логических элементов, т. к. эти функции и их аргументы могут иметь только два значения: 0, 1.

2. Разработка цифрового (логического) устройства начинается со словесной формулировки алгоритма его работы. Затем составляется таблица истинности, которая учитывает все возможные сочетания влияющих факторов (аргументов) и соответствующие им значения функции. После этого, на основе таблицы, составляется совершенная дизъюнктивная нормальная форма для записи аналитического выражения. Затем, при необходимости, осуществляется минимизация и, наконец, реализация в виде устройства.

3. Одни логические функции можно выражать с помощью других логических функций для их минимизации и упрощения технической реализации.

4. Цифровые устройства могут применяться для решения различных задач, с использованием разнообразных аппаратурных средств (диодов, контактов, реле, микросхем). Например, в релейной защите, автоматике, цифровой технике и т.д.

5. Булева алгебра лежит в основе любых логических рассуждений, доказательств и используется, например, при доказательстве теорем, конструировании устройств цифровой и вычислительной техники, в алгоритмических языках и т. д.