Законы алгебры логики. Последовательность выполнения операций в алгебре логики

1.4 Законы алгебры логики

Последовательность выполнения операций в алгебре логики: при наличии скобок сначала осуществляются операции внутри них, затем инверсии, после логические умножение и, затем, сложение (таблица 1.4.1).

Эквивалентность выражений в алгебре логики проверяется с помощью составления таблицы истинности для всех возможных наборов переменных, значения которых для сравниваемых выражений должны быть одинаковы.

Законы алгебры логики на примере логических функций И, ИЛИ                         Таблица 1.4.1

Переместительный
Сочетательный
Распределительный

1.4.1 Свойства логических функций (таблицы 1.4.2 ..1.4.6)

Свойства логических функций ИЛИ, И, НЕ                                                               Таблица 1.4.2

ИЛИ	И	НЕ

Правила и тождества  для функций И, ИЛИ, НЕ                                                       Таблица 1.4.3

Тождества операций И, ИЛИ
Правило Де Моргана для операций И, ИЛИ
Правило поглощения

Правила и тождества  для функций И, ИЛИ, НЕ (продолжение)                    

Склеивания

Законы алгебры логики для логической функции исключающее ИЛИ                  Таблица 1.4.4

Переместительный
Сочетательный
Распределительный

Свойства функций исключающее ИЛИ и эквивалентности                                     Таблица 1.4.5

Определение операции
Правило Де Моргана
Свойства
Тождества

Свойства функций стрелка Пирса, штрих Шеффера                                                 Таблица 1.4.6

Определение операций «/», «¯»
Правило Де Моргана
Свойства

1.4.2 Суперпозиция

подстановка в логические функции вместо переменных других логических выражений позволяет получить функции желательного числа переменных, например:

 

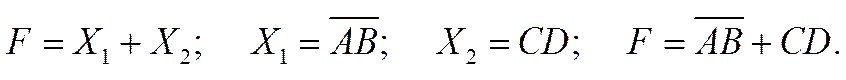1.4.3 Принцип двойственности

Из таблицы 1.3.2 следует, что у функций с взаимно дополняющими номерами i  и 15 – i значения для одинаковых наборов переменных являются инверсными друг к другу. В тоже время, инверсия всех значений функции – инверсия самой функции.

Пример для функций F₇ и F₈; F₆ и F₉:

 

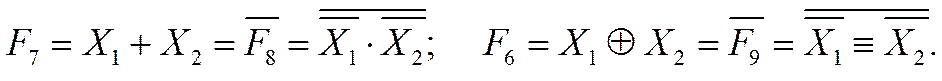Следовательно, при переходе от одной операции к другой (с взаимно дополняющими номерами) все переменные и выражение в целом должны инвертироваться.

Частный случай этого принципа – правило Де Моргана.

1.4.4 Примеры использования правил алгебры логики

Пример: преобразование логических операций и доказательство справедливости с помощью таблицы истинности.

 

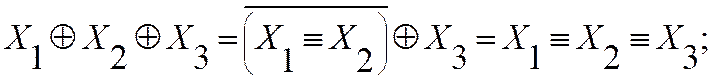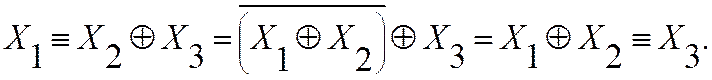Произошла замена операции сложения по модулю два на операцию эквивалентности и наоборот, что справедливо для любого нечетного количества переменных (в преобразованиях использовались тождества и определение операций).

Проверка справедливости первого аналитического выражения с помощью таблицы истинности (таблица 1.4.7):

Таблица истинности                                                                                               Таблица 1.4.7

№	X1	X2	X3
0	0	0	0	0	0	0
1	0	0	1	1	1	1
2	0	1	0	1	1	1
3	0	1	1	0	0	0
4	1	0	0	1	1	1
5	1	0	1	0	0	0
6	1	1	0	0	0	0
7	1	1	1	1	1	1

Например, для набора № 0 (первая строка), где все переменные равны логическому нулю, имеем:

 

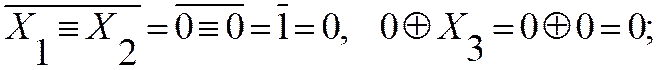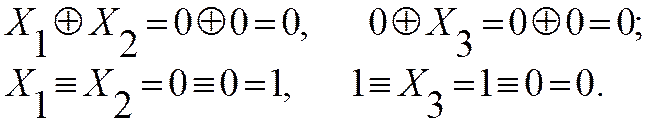Следовательно, на данном наборе (как и на других) выполненные преобразования верны.

Пример: доказать правило поглощения в аналитическом виде.

 

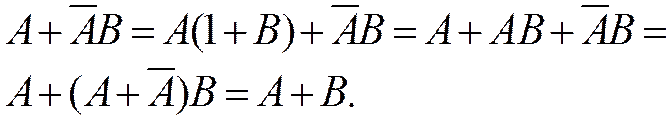Пример: упросить аналитическое выражение, используя законы алгебры логики:

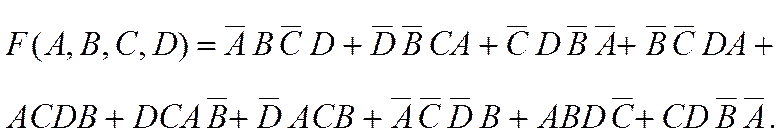
1-й шаг. На основании переместительного закона во всех членах выражения размещаем переменные в одном и том же порядке (подчеркивание снизу для обозначения переменных, которые будут группироваться в следующем шаге):

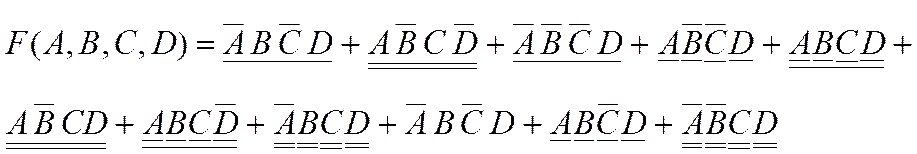
2-й шаг. Группируем члены таким образом, чтобы в каждую пару входили переменная, и ее инверсия:

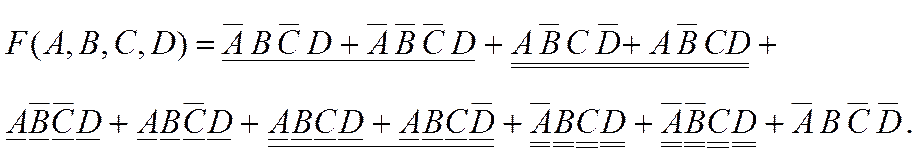
3-й шаг. Руководствуясь распределительным законом, в каждой группе выносим за скобку одинаковые переменные:

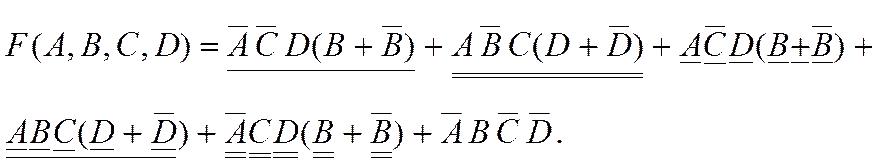
4-й шаг. Согласно свойствам логических функций (закон дополнения) имеем:

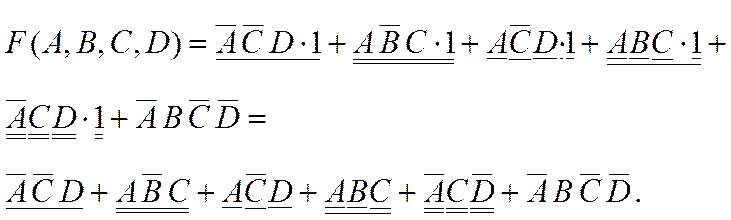
5-й шаг. Выполняя аналогичные преобразования, получаем:

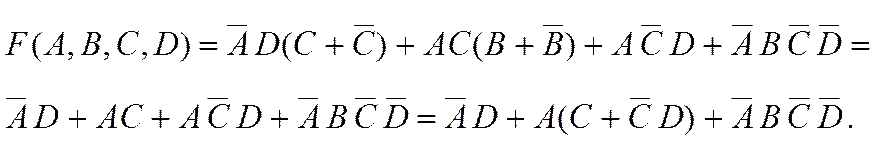
6-й шаг. На основании закона поглощения пишем:

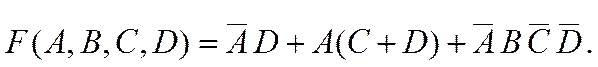
7-й шаг. Применив распределительный и сочетательный законы, имеем:

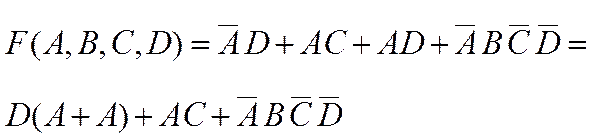
и, учитывая, что получаем:

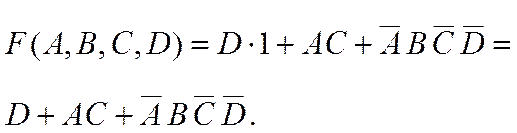
8-й шаг. В соответствии с сочетательным законом запишем:

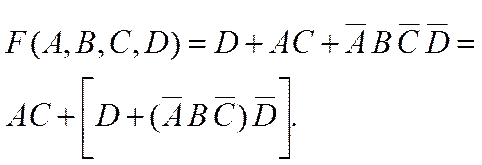
Но по правилу поглощения:

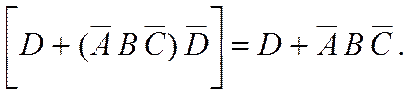
Следовательно,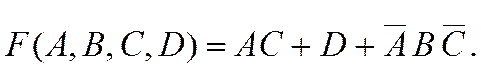

9-й шаг. Применив переместительный и сочетательный законы, имеем:

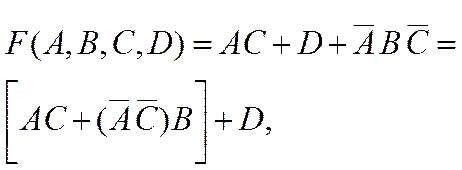
откуда по правилу поглощения: