Работа с лазером: Теоретические сведения и порядок выполнения работы, страница 2

Такие и подобные им явления, когда характеристики вещества обратимым образом изменяются под действием света, причем тем сильнее, чем выше интенсивность света, изучает раздел современной оптики, называемый нелинейной оптикой.

Нелинейность оптических свойств вещества связана с его электрической поляризацией. Оптические кристаллы являются диэлектриками. Под действием внешнего электрического поля диэлектрики поляризуются: поле вызывает смещение электронных оболочек атомов относительно ядер вещества диэлектрика. В результате этого атомы приобретают электрический дипольный момент. Поляризация единицы объема среды Р связана с напряженностью поляризующего электрического поля Е соотношением ('опись для плоских волн):

Р = о£

1дссь и - дюлеюрическая проницаемость данного вещества, т.е. величина , которая характеризует

ПОЛЯршуемОСГЬ зтого вещества. Таким соотношением описывается поляризация диэлектрика под

к¹ id ткем C.I.KH/II снеговой водны. Здесь зависимость линейная. Под воздействием мощного светового поля лазера поляризация диэлектрика во многих случаях зависит от этого поля нелинейным образом и

описывается соотношением;

P = cjc_oE+a,E² + a_:E³+...

Такое поведение поляризации оптических кристаллов порождает ряд новых "нелинейных оптических явлений", таких как получение гармоник (второй, третий, четвертый...), самофокусировка, параметрическая генерация.

В нелинейной оптике мы имеем дело с принципиально новой ситуацией. Если интенсивность света велика, чтобы проявлялась нелинейность электрической поляризации среды, то в такой среде можно наблюдать взаимодействие световых волн. В результате такого взаимодействия могут возникать новые световые волны Взаимодействие световых волн с частотами \ i и v_; может приводить к возникновению световых волн на частотах 2vi , 2v₂, v, + v₂, v, - v;JB этом можно убедиться, если представить сумму двух плоских волн в виде:

Eocos27tv,t + E₀cos2rcv-.t = E₀|cos27tvi( + cos2jtv-.tl и возвести ее_ в квадрат, то после тригонометрических преобразовании суммы косинусов для электрической поляризации среды получим слагаемые косинусы с указанными выше частотами: гармоники, суммы и разности частот.

В частном случае предположим, что в среде с нелинейной поляризацией распространяется волна частоты v. Она вызывает в среде вторичную волну этой же частоты в соответствии с принципом Гюйгенса. Другими словами, в нелинейной среде волна частоты v взаимодействует сама с собой. В соответствии с вышеизложенным возможно переизлучение волны v в волну с частотой 2v, т.е. мы подучаем 2-ю гармонику воздействующей волны.

Для эффективной передачи энергии от исходной световой волны частоты v к переизлученной световой волне частоты 2ч^г необходимо, чтобы скорости обеих волн v (v) и v (2v) могли совпадать. Простая аналогия: нельзя на бегу передавать непрерывно что-то партнеру, если его скорость не равна вашей. Скорость света в среде равна скорости света в вакууме, деленной на показатель преломления среды V_cp=C/n_cp . Значит, показатели преломления для рассматриваемых световых волн n_v и n_2v должны быть равны. Но показатель преломления обычно вырастает с частотой света и условие n(v) = n(2v) кажется невыполнимым. Оказывается . это условие может быть выполнено, если использовать особенности прохождения света через нелинейные кристаллы, обладающие двулучепреломлением

..Напомним некоторые свойства таких кристаллов.

В кристалле существует особое направление, которое называется оптической осью кристалла. Дтя всех направлений, составляющих один и тот же угол с оптической осью и вдоль оси, свойства кристалла

одинаковы. Плоскость, проходящая через оптическую ось и направление распространения световой волны, называется плоскостью главного сечения. Световая волна, попадая в кристалл, превращается в две волны, которые имеют разные скорости распространения в кристалле и разные поляризации. Одна волна называется обыкновенной. Электрический вектор этой волны "протыкает" главную плоскость. Для второй волны - необыкновенной, электрический вектор лежит в главной плоскости. Для обыкновенной волны показатель преломления не зависит от направления ее распространения, для необыкновенной волны он зависит от направления. Необыкновенный луч отклоняется в сторону при распространении через кристалл. Пусть показатель преломления для обыкновенной волны п°, а для необыкновенной п^е и он зависит от угла О между направлением распространения волны и оптической осью кристалла

На первой схеме (Рис.1) представим сечение нелинейного кристалла плоскостью, проходящей через оптическую ось ОА.

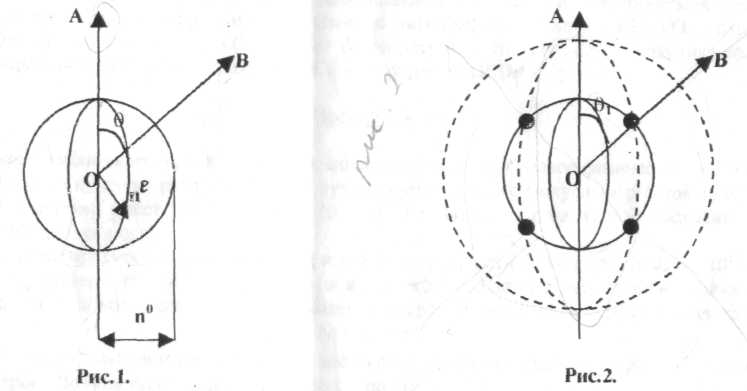
Теперь мы имеем воображаемую картину величин показателей преломления кристалла. Круг в сечении - это показатель преломления для обыкновенной волны: в любом направлении показатель преломления одинаков и равен п°. Для необыкновенной волны показатель преломления п^е (0) является ф] iiKuifcn \i.ia и между оптической осью ОА и направлением распространения необыкновенного луча. Из

I ■ и i......го к имршлешш оптической оси м°= п^е. по всем другим направлениям они не совпадают (n^u

\ч пи   \одит по Кругу, п^с "ходит" эллипсу).

11л второй схеме (рис. 2) показаны в сечении поведение показателя преломления для обыкновенной и необыкновенной волн для некоторой часто) ы v и 2v, т.е. для второй гармоники некого нелинейного кристалла, находящегося под воздействием сильного светового поля частоты v. Из-за электрической поляризации среды показатели преломления для обыкновенной и необыкновенной волн возраелн. Однако, можно увидеть, что есть направление в кристалле, где показатели преломления п°« = a'zv(6i) (штриховой эллипс и сплошной круг пересекаются в точке по направлению ОВ). А это условие, как следует из ранее изложенных рассуждений, является условием, когда происходит эффективная передача энергии из волны частоты v к переизлученной волне частоты 2\\ т.е. второй гармонике/ Приведенное условие равенства показателей преломления п\ = n^c;_v называется "условием волнового синхронизма". Направление ОВ по схеме называется направлением синхронизма, а угол В между этим направлением и осью кристалла называют углом синхронизма.

Из приведенного рассуждения можно сделать выводы о том , как на практике нужно осуществить схемы получения второй гармоники. На ниже приведенной схеме показан разрез нелинейного кристалла, который обеспечивает получение второй гармоники.

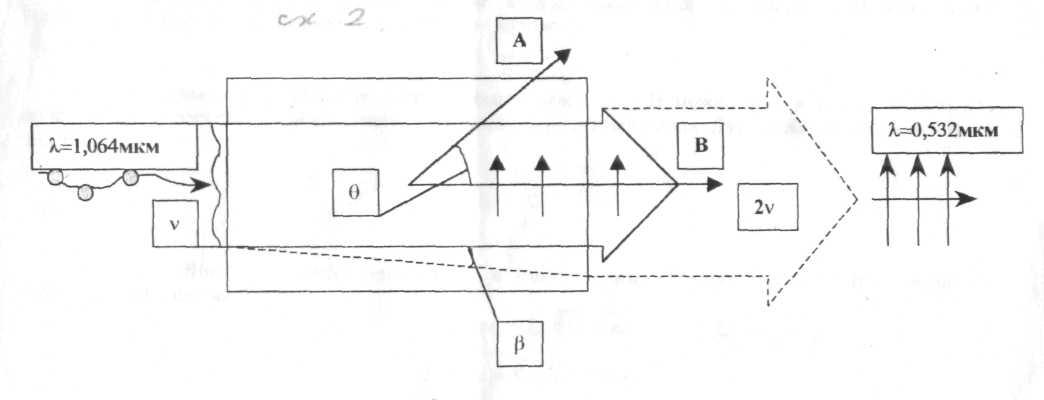
Кристалл вырезан так, что направление синхронизма" ОВ совпадает с длиной кристалла, а оптическая ось кристалла ОА расположена к направлению синхронизма (к направлению распространения луча) под утлом синхронизма 9. Излучение частоты v преимущественно поляризованное перпендикулярно к плоскости чертежа (обыкновенная волна) вызывает в кристалле электрическую поляризацию и порождает волну частоты 2v, поляризация ("оптическая"!) которой "лежит" в плоскости чертежа. Из-за двойного лучепреломления происходит отклонение необыкновенной волны на угол (3 от оси распространения (снос луча). Снос отсутствует, если угол синхронизм;! О = 90° (такие кристаллы бывают - 90° синхронизм- •').