Измерение диаметра гауссовых пучков: Физический практикум

Министерство общего и профессионального

Образования Российской Федерации

                 Новосибирский государственный технический университет

Кафедра лазерных систем

ФИЗИЧЕСКИЙ ПРАКТИКУМ

ИЗМЕРЕНИЕ ДИАМЕТРА ГАУССОВЫХ ПУЧКОВ

Факультет: Физико-технический

Группа:

Студент:

Преподаватель:

Новосибирск 2005

Введение

Считается, что наиболее энергетически выгодным и стабильным режимом работы лазера является тот, при котором излучается один основной поперечный тип колебаний. При этом режиме пространственное распределение энергии (мощности) излучения описывается нормальным законом Гаусса.

       В лазерах с брюстеровской оптикой диафрагмы, ограничивающие вертикальный и горизонтальный размеры пучка, могут слегка различаться, что приводит к гауссовому профилю с различными радиусами в вертикальной и горизонтальной плоскостях. Такой профиль пучка нельзя считать оптимальным.

        Таким образом, измерение пространственных профилей лазерного пучка часто бывает необходимо  при настройке лазера и выводе его на максимальную мощность.

        Различные применения оптических квантовых генераторов в физических исследованиях, медицине и технике также требуют регистрации пространственного распределения плотности мощности излучения по поперечному сечению пучков: измерения диаметров лазерных пучков, измерения энергетической расходимости.

         Точное измерение радиуса пучка в фокусе  необходимо для вычисления радиуса сфокусированного пучка на разных расстояниях от фокуса линзы и  вычисления интенсивности излучения в фокусе.

        Существует много способов реализации подобных измерений.  Можно выделить два основных  подхода:

1)  сканирующие системы, в которых через поперечное сечение пучка продвигается точечная диафрагма (pinhole), фотоприемник с малой входной апертурой, или нож, обрезающий часть светового пучка. Такие системы могут обладать довольно высокой точностью и работать с пучками разной интенсивности и размеров, но они достаточно, инерционные  и не позволяют работать в режиме реального времени;

2)  двухкоординатные детекторы с пространственным разрешением – пленочные визуализаторы: люминофоры, жидкие кристаллы, полупроводниковые пленки. Такие системы позволяют определить диаметр пучка, но для измерения распределения интенсивности по профилю пучка требуют дополнительных средств оцифровывания сигналов. После появления  двухмерных фотодиодных матриц, содержащих нескольких сот элементов, стало возможным работать в режиме реального времени. Пространственное разрешение подобных систем определяется числом элементов. 

      В 1982 году был получен патент США  на устройство для регистрации пространственного профиля лазерного пучка с помощью двухмерной фотодиодной матрицы Reticon RA-32x32. В настоящее время подобные устройства выпускаются серийно.

 Особые трудности вызвала эта проблема при измерении профиля излучения СО₂ – лазеров, так как в этом случае не могут быть использованы регистрирующие среды, традиционные для видимой и ИК-областей.

1.  Теоретическая часть

        Параметры гауссовских пучков полностью определяются заданием одной величины – радиуса пучка в «перетяжке» - w₀. В перетяжке пучка волновой фронт является плоским.

         При известном значении w₀  радиус пучка  w в плоскости, отстоящей от «перетяжки» на расстоянии Z для излучения с длиной волны l, может быть найден по формуле:

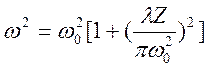                                              (1)

         Радиус кривизны волнового фронта R на расстоянии Z от «перетяжки»:

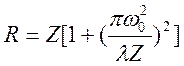                                                                             (2)

         Распределение амплитуды поля в этой плоскости описывается выражением:

                               (3)

где  х и  у – координаты в плоскости, перпендикулярной направлению распространения пучка.

        Для интенсивности излучения имеем выражение:

                              (4)

2. Экспериментальная часть

Знакомство с работой оптического анализатора «Ангстрем»

        Оптический анализатор «Ангстрем» предназначен для регистрации спектров оптического излучения. В качестве приемной части прибора используется оптоволокно  разной толщиной.

        Оптический анализатор состоит из оптического блока: система зеркал, дифракционная решетка и фотодиодная линейка Sony ILX511, платы сбора и обработки данных в виде платы расширения к персональному компьютеру и программного обеспечения. Анализатор позволяет регистрировать как спектры излучения в диапазоне длин волн от 350 до 950 нм, так и интенсивность на заданной длине волны или интервале длин волн с временным разрешением в 1 с и более.

Шаг - 20 мкм

Были получены следующие результаты:

№ шага		№ шага		№ шага		№ шага
1	30	36	80	71	970	106	510
2	30	37	85	72	980	107	470
3	30	38	100	73	1080	108	400
4	30	39	110	74	1100	109	360
5	30	40	120	75	1140	110	320
6	30	41	130	76	1160	111	300
7	30	42	140	77	1180	112	270
8	40	43	160	78	1220	113	260
9	40	44	170	79	1240	114	250
10	40	45	180	80	1260	115	230
11	40	46	200	81	1300	116	220
12	40	47	220	82	1320	117	220
13	40	48	230	83	1340	118	210
14	40	49	250	84	1360	119	200
15	40	50	270	85	1380	120	200
16	40	51	300	86	1400	121	195
17	40	52	330	87	1420	122	180
18	35	53	360	88	1430	123	170
19	30	54	420	89	1440	124	160
20	30	55	440	90	1460	125	150
21	40	56	450	91	1470	126	140
22	30	57	430	92	1450	127	130
23	30	58	470	93	1450	128	120
24	30	59	510	94	1400	129	110
25	30	60	600	95	1360	130	110
26	30	61	640	96	1200	131	100
27	30	62	660	97	1200	132	90
28	30	63	680	98	1100	133	70
29	40	64	700	99	1000	134	60
30	40	65	800	100	960	135	60
31	40	66	860	101	860	136	50
32	40	67	890	102	800	137	40
33	50	68	900	103	730	138	40
34	60	69	920	104	640	139	40
35	65	70	960	105	560	140	40

В связи с результатами был построен график профиль гауссовского пучка.

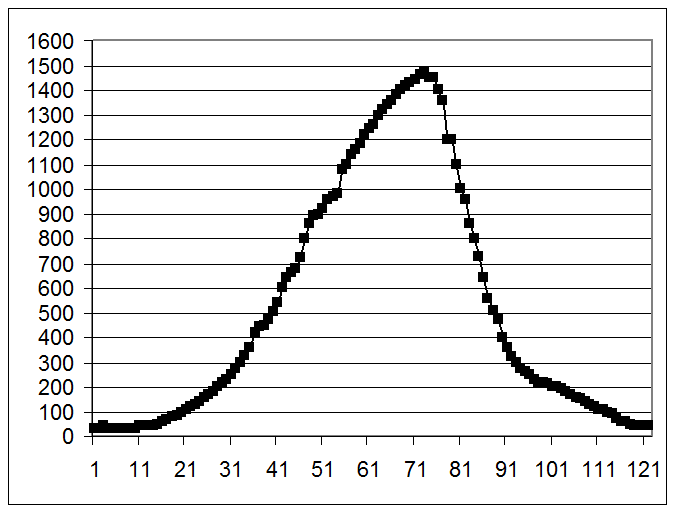
        При известном значении w₀  радиус пучка  w в плоскости, отстоящей от «перетяжки» на расстоянии Z для излучения с длиной волны l, может быть найден по формуле:

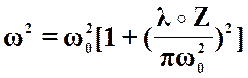
Величина z в данном эксперименте равна 2см, величина l равна 632нм. Для того чтобы найти радиус пучка в перетяжке нам необходимо знать радиус пучка на расстояние z. Эту величину можно рассчитать, исходя из полученных данных.

Найдем разницу между максимумом и минимумом интенсивности:

 I = Imax – Imin = 1470 – 40 = 1430;

Найдем значение интенсивности на уровне 0.15:      

 0.15I = I*0.15 = 1430* 0.15 = 214.5;

 I + 0.15I = 214.5 +1430 = 1644;

Найдем радиус пучка на расстояние z:

w=  (98 – 31)*20 мкм =  0.134 см;

        

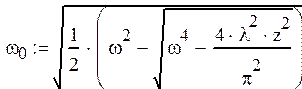
w₀=2,96 мкм

Вывод:

Значение радиуса гауссова пучка в перетяжке по порядку величины

совпадает