Технологический процесс обработки шеек коленчатого вала, страница 6

          В таблице 4 координаты характерных точек кривой нормального распределения определяются по формулам:

Вершина кривой:         f =0.4 (nc/s)

Точки перегиба : f_s=0.242 (nc/s)     

                             f_2s=0.242 (nc/s)

f_3s=0.

Таблица 4. Координаты характерных точек кривой нормального распределения

          В таблице 4 и 5:

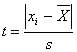 и 5

          Для вычисления теоретических частот составим таблицу 6.

Значения t вычислены по формуле:

, где х_нб – верхнее значение интервала.

Значения f ‘  вычислены по формуле:

.

Значения интегральной функции F(x)  вычислены по формуле:

. Ф(t) определяются по таблицам.

Таблица 6. Вычисление теоретических частот нормального распределения при  помощи функции  Ф(t)