Моделирование электродвигателя постоянного тока последовательного возбуждения

Министерство образования Республики Беларусь

Гомельский государственный технический университет

имени П. О. Сухого

Кафедра «Автоматизированный электропривод»

ОТЧЁТ

по лабораторной работе №2

«Моделирование электродвигателя постоянного тока последовательного возбуждения»

                       Выполнил студент гр. ЭП – 31:

                       Швецов Е.В.

                       Проверил преподаватель:

                       Захаренко В.С.

Гомель 2011

Цель работы: 

– ознакомиться с алгоритмами моделирования статических элементов систем автоматического управления;

– ознакомиться с приемами моделирования динамических элементов;

– получить практические навыки составления программ моделирования.

Ход работы

21. Швецов Евгений Викторович

Двигатель Д12, тихоходное исполнение, последовательное возбуждение.

Структурное моделирование. Метод Эйлера.

Используя справочные данные, определяем параметры заданного двигателя:

Напряжение на обмотке якоря

:  220

Число параллельных ветвей якоря:  2

Сопротивление якоря и добавочных полюсов:   1,63

Номинальный ток двигателя:  15

Частота вращения ротора двигателя:  1150

Число пар полюсов:  2

Число активных проводников якоря:  990

Инерция якоря:  0,05

Магнитный поток на полюс:  0,45

Шаг расчета:  0,0005

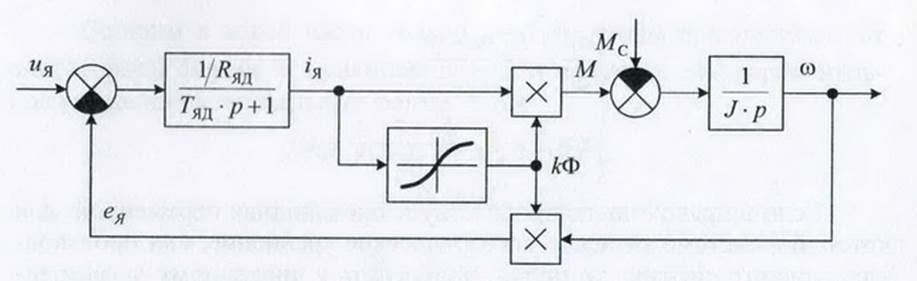
Рис. 1   Структурная схема двигателя постоянного тока последовательного возбуждения без учета фиктивной обмотки вихревых токов.

На рис. 1 обозначено:

uЯ - напряжение на якорной цепи двигателя;

еЯ - ЭДС якоря;

iЯ - ток якоря двигателя;

k · ФВ - произведение конструктивной постоянной двигателя на поток возбуждения;

f(iВ) - функция, отражающая нелинейную зависимость потока возбуждения от тока обмотки возбуждения (для ДПТ ПВ iЯ = iВ);

mДВ - момент двигателя;

mC - момент сопротивления;

ω - угловая скорость вращения двигателя;

RЯ и TЯ - сопротивление и постоянная времени якорной цепи;

J - момент инерции якоря.

Кривую намагничивания для двигателей серии Д можно аппроксимировать кусочно-линейной функцией, представленной на рис. 2.

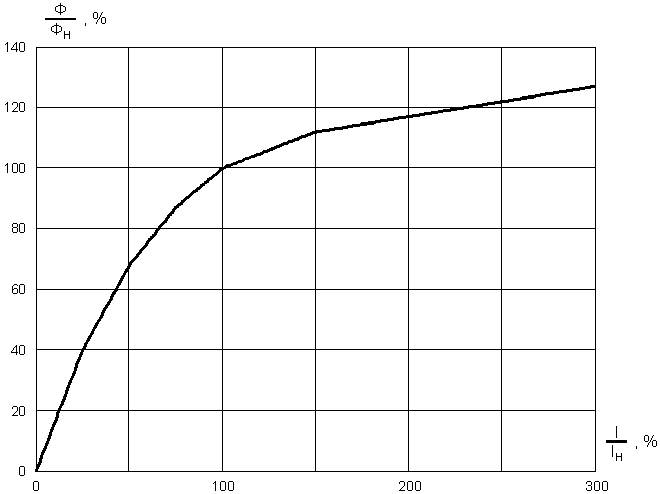
Рис. 2. Кусочно-линейная функция

 По осям отложены относительные значения тока и потока двигателя (отнесенные к номинальным значениям). Координаты конечных точек отрезков:

(0%; 0%).                       (75%; 87%).                    

(25%; 40%).                   (100%; 100%).   

(50%; 68%).                   (150%; 112%).

 Последний участок характеристики - луч проходящий через точку (250%; 122%).

1.  Интегрирующее звено.

                 Выходной сигнал звена в операторной форме:

y(p)=1/T*p*x(p)

Составим дифференциальное уравнение для выходного сигнала:

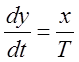
Алгебраическое уравнение согласно методу Эйлера:

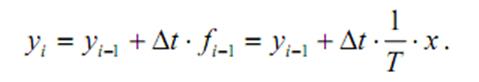
2.  Апериодическое звено.

Выходной сигнал звена в операторной форме:

y(p)=K*x(p)/( T*p+1)

Составим дифференциальное уравнение для выходного сигнала:

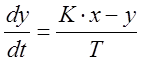
Алгебраическое уравнение согласно методу Эйлера:

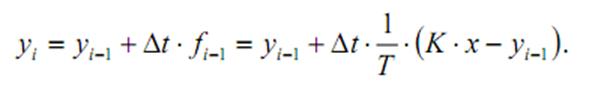
3.  Множительное звено.

Описывается выражением:

Y = X1*X2

4.  Вычитательное звено.

Описывается выражением:

Y = X1 - X2

Таблица описания переменных:

Переменная	Описание
u_nom	Напряжение на обмотке якоря
a	Число параллельных ветвей якоря
r_z	Сопротивление якоря и добавочных полюсов
I_n	Номинальный ток двигателя
n_ob	Чаcтота вращения ротора двигателя
p	Число пар полюсов
N	Число активных проводников якоря
J	Инерция якоря
F_n	Магнитный поток на полюс
dt,  t	Интервал и шаг расчета, текущее время
t_start, t_full, t_stop	Время пуска, работы пи торможения
M_nom	Номинальный момент
T_z	Постоянная времени якорной цепи
y, yp	Значения переменных модели, для которых есть дифференциальные уравнения, на текущем и предыдущем шагах расчета, соответственно

Кодпрограммы:

Type

  DArray=array[1..7] of double;

procedure TForm1.Button4Click(Sender: TObject);

begin

close;

end;

procedure TForm1.Button2Click(Sender: TObject);

var

a,k,k1,n_ob,p,U_nom,w,I_n,t_start,t_full,t_stop,

n,r_z,alpha,L_z,F_n,T_z,M_nom,J,t,dt:double;

y,yp:darray;

i,kol:integer;

function Moment(t,M_nom:double):double;

var

M:double;

begin

if t<=0 then M:=0

       else if t<t_start then M:=0.5*M_nom

               else if t<t_full then M:=M_nom

               else M:=M_nom;

Moment:=M;

end;

function u(t,U_nom:double):double;

begin

u:=0;

if t<=0 then u:=0

       else if t<t_start then u:=u_nom

       else if t<t_full then u:=u_nom

       else if t<t_stop then u:=0;

end;

function sign(x:double):double;

begin

if x>0 then sign:=1

       else

       if x=0 then sign:=0

              else sign:=-1;

end;

function flux(i_1:double):double;

var

  i0,kf0,S:double;

begin

S:=sign(i_1);

i_1:=abs(i_1);

i0:=i_1/I_n;

if i0<=0.25 then kf0:=0.4/0.25*i0

           else if i0<=0.5 then kf0:=0.4+(0.28/0.25)*(i0-0.25)

               else if i0<=0.75 then kf0:=0.68+(0.19/0.25)*(i0-0.5)

                   else if i0<=1 then kf0:=0.87+(0.13/0.25)*(i0-0.75)

                       else kf0:=1+(0.12/0.5)*(i0-1);

flux:=s*kf0*k*F_n;

end;

function sum(x,y:double):double;

begin

sum:=x-y;

end;

function multiplier(x,y:double):double;

begin

multiplier:=x*y;

end;

function ap(x,yp,k,T_z:double):double;

var

  y:double;

begin

  y:=yp+dt*(k*x-yp)/T_z;

  y:=yp+dt/2*(((k*x-yp)/T_z)+((k*x-y)/T_z));

  ap:=y;

end;

function int(xp,yp,t:double):double;

var

  y:double;

  i:integer;

begin

  for i:=1 to 2 do

  y:=yp+dt*xp/t;

  int:=y;

end;

procedure scheme(yp:darray;t:double;var y:darray);

var

m,U_z:double;

begin

U_z:=u(t,U_nom);

M:=Moment(t,M_nom);

y[1]:=sum(U_z,y[7]);

y[2]:=ap(y[1],yp[2],k1,T_z);

y[3]:=multiplier(y[2],y[6]);

y[4]:=sum(y[3],M*sign(y[5]));

y[5]:=int(y[4],yp[5],t);

y[6]:=flux(y[2]);

y[7]:=multiplier(y[6],y[5]);

end;

begin

bar2.Progress:=0;

a:=strtofloat(Edit_2a.text);

n_ob:=strtofloat(Edit_n_ob.text);

p:=strtofloat(Edit_p.text);

u_nom:=strtofloat(Edit_u.text);

r_z:=strtofloat(Edit_r.text);

J:=strtofloat(Edit_J.text);

I_n:=strtofloat(Edit_I_n.text);

N:=strtofloat(Edit_n.text);

F_n:=strtofloat(Edit_F_n.text);

dt:=strtofloat(Edit_dt.text);

F_n:=0.01;

w:=3.14*n_ob/30;

alpha:=0.0039;

r_z:=r_z*(1+alpha*(160-20));

L_z:=0.6*U_nom/(p*w*I_n);

k:=p*N/(3.14*a);

T_z:=L_z/R_z;

M_nom:=k*F_n*I_n;

k1:=1/r_z;

t_start:=3;

t_full:=t_start+2;

t_stop:=t_full+1;

kol:=round(t_stop/dt);

bar2.MaxValue:=kol;

fillchar(y,sizeof(y),0);

fillchar(yp,sizeof(yp),0);

Form3.Series1.Clear;

Form3.Series2.Clear;

Form2.series1.clear;

t:=0;

Form3.Series1.AddXY(t,y[2]);

Form3.Series2.AddXY(t,y[5]);

Form2.Series1.AddXY(y[2],y[5]);

bar2.Visible:=true;

for i:=1 to kol do

  begin

  bar2.Progress:=i;

  t:=dt*i;

  scheme(yp,t,y);

  Form3.Series1.AddXY(t,y[2]);

  Form3.Series2.AddXY(t,y[5]);

  Form2.Series1.AddXY(y[2],y[5]);

  yp:=y;

  end;

Button3.visible:=true;

Button1.Visible:=true;

bar2.Visible:=false;

end;

procedure TForm1.Button3Click(Sender: TObject);

begin

Form3.showmodal;

end;

procedure TForm1.Button1Click(Sender: TObject);

begin

Form2.ShowModal;

end;

end.

График переходных процессов

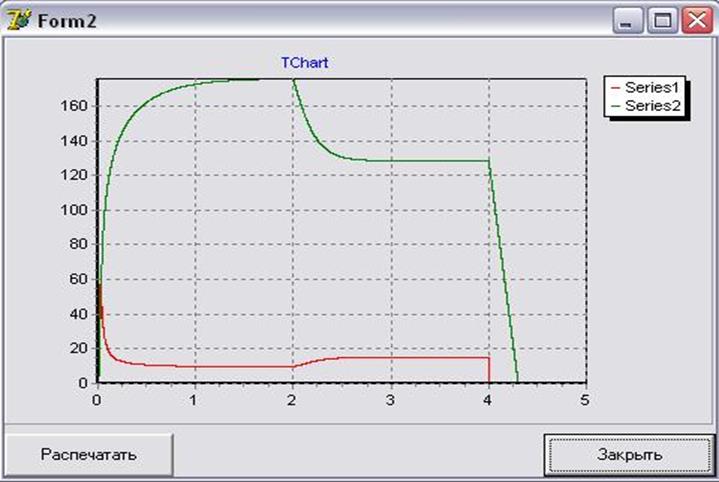
График динамических процессов

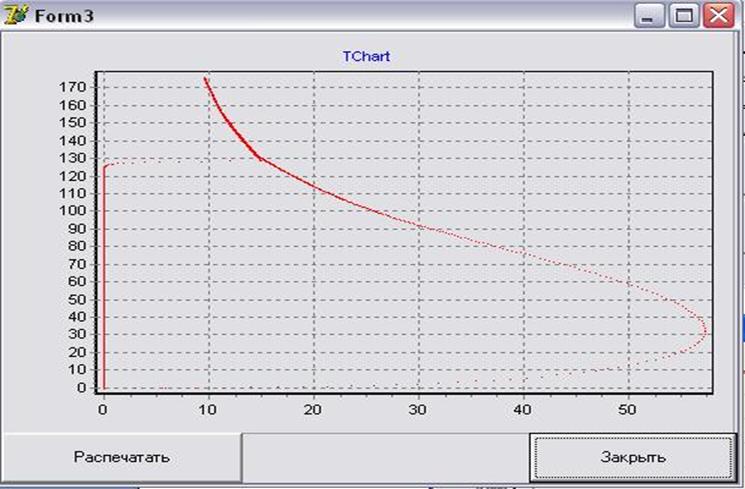
Вывод:

Ознакомился с алгоритмами моделирования статических элементов систем автоматического управления, ознакомился с приемами моделирования динамических элементов, получил практические навыки составления программ моделирования.