


Определение
величины гиромагнитного отношения 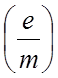 электрона
электрона
Курбатова Л.М.
г. Гомель, 2002
Определение
величины гиромагнитного отношения 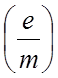 электрона
электрона
2. Определить величину
гиромагнитного отношения 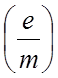 электрона.
электрона.
Приборы и принадлежности: Панель с лампой «коаксиальный диод», катушки Гельмгольца, два источника питания УИП-2, соединительные провода и кабель.
1. В процессе движения частицы меняется величина и направление ее скорости. Рассмотрим ее движение на нескольких этапах, отличающихся величиной угла «α» между направление скорости частицы и радиальным направлением электрического поля. Величину скорости удобнее найти из закона сохранения энергии, выразив ее как функцию удаления от оси:
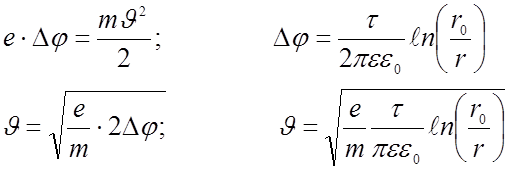
Сначала эта сила мала, но растет вместе с величиной скорости частицы, а потому при малых углах «α» растет и кривизна траектории, определяется из 2 закона Ньютона:
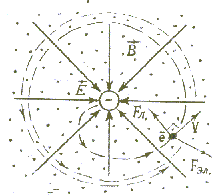
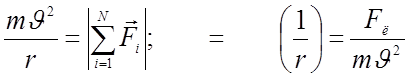
В итоге частица движется по сложной спирали, которая постепенно приближается к окружности, центр которой лежит на оси симметрии электрического поля.
2. Выше приведен анализ движения показывает, что в заданных скрещенных полях частица не может выйти за пределы окружности некоторого радиуса, величина которого зависит от характеристики электрического и магнитного полей.
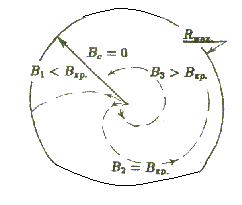
Изменяя магнитную индукцию поля можно уменьшить предельный радиус кривизны траектории и довести его заранее заданной величины.
Схема подключения:
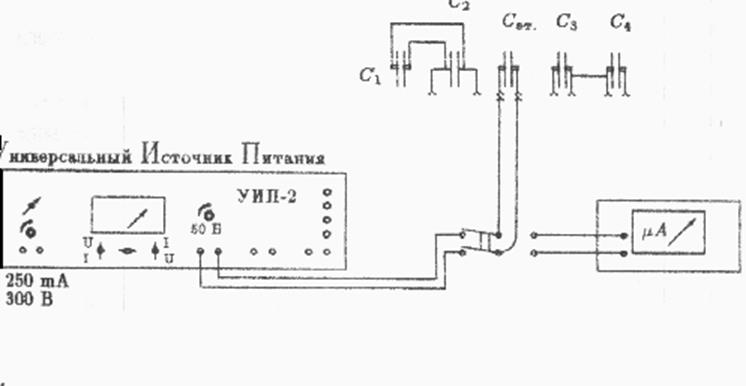
Ход работы
1. Измеряем ток соленоида, записываем его вместе с анодным током лампы и все данные вносим в таблицу:
|
Ic,мА |
30 |
99 |
155 |
190 |
210 |
220 |
230 |
240 |
250 |
|
Iа,мА |
50 |
49 |
48 |
47 |
45 |
40 |
35 |
30 |
25 |
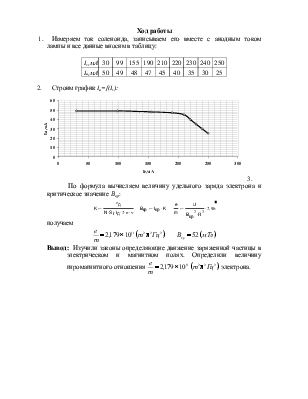
2. Строим график Iа=f(Ic):
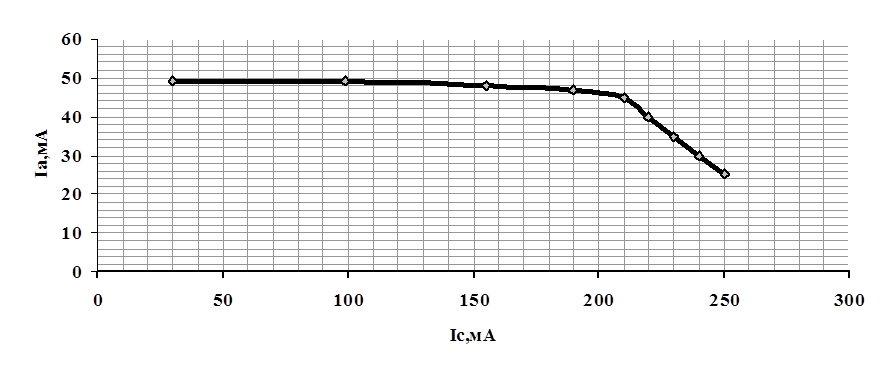 3. По формула вычисляем величину
удельного заряда электрона и критическое значение Вкр:
3. По формула вычисляем величину
удельного заряда электрона и критическое значение Вкр:
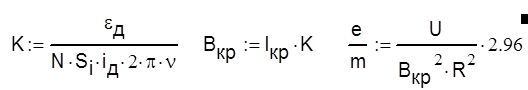
получаем
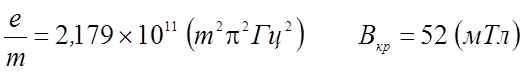
 электрона.
электрона.Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.